
- •50. Что выражает функция Беллмана в задаче о замене оборудования?
- •51. Запишите рекуррентные соотношения Беллмана для задачи о замене оборудования.
- •1. Двойственная задача лп.
- •2. Экономическая интерпретация двойственной задачи.
- •3. Основные соотношения двойственности.
- •4. Предварительный анализ оптимального решения задачи линейного программирования.
- •5. Чувствительность целевой функции к изменениям ограничений.
- •6. Устойчивость оптимального базисного плана к изменениям ограничений.
- •7. Транспортная задача: постановка задачи.
- •8. Транспортная задача: понятие базисного плана перевозок.
- •9. Методы построения начального базисного плана.
- •10. Распределительный метод решения транспортной задачи. Проверка достаточных условий оптимальности
- •11. Распределительный метод решения транспортной задачи. Вычисление максимально допустимой циркуляции.
- •12. Метод потенциалов решения транспортной задачи.
- •13. Задача целочисленного линейного программирования: постановка, подходы к разработке методов.
- •14. Метод ветвей и границ: общая схема.
- •15. Решение целочисленной задачи линейного программирования методом ветвей и границ.
- •16. Алгоритм Гомори: построение правильного отсечения, его присоединение к симплексной таблице, выбор разрешающей строки и ведущего столбца.
- •17. Динамическое программирование: предмет исследования, математическая модель многошагового процесса.
- •18. Задача распределения ресурсов: постановка и анализ (вывод соотношений Беллмана).
- •19. Задача о замене оборудования: постановка и анализ (вывод соотношений Беллмана))
11. Распределительный метод решения транспортной задачи. Вычисление максимально допустимой циркуляции.
Построим
цикл
![]() ,
который образует клетка (i*,j*)
с базисными клетками таблицы, и разметим
его знаками «+» и «-». Изменим объем
поставки от i*
-го
поставщика к
j*-му
потребителю на величину циркуляции Θ>0
и рассмотрим изменения, произошедшие
в клетках цикла
,
который образует клетка (i*,j*)
с базисными клетками таблицы, и разметим
его знаками «+» и «-». Изменим объем
поставки от i*
-го
поставщика к
j*-му
потребителю на величину циркуляции Θ>0
и рассмотрим изменения, произошедшие
в клетках цикла
![]() ,
обозначив через
,
обозначив через
![]() измененные объемы поставок:
измененные объемы поставок:
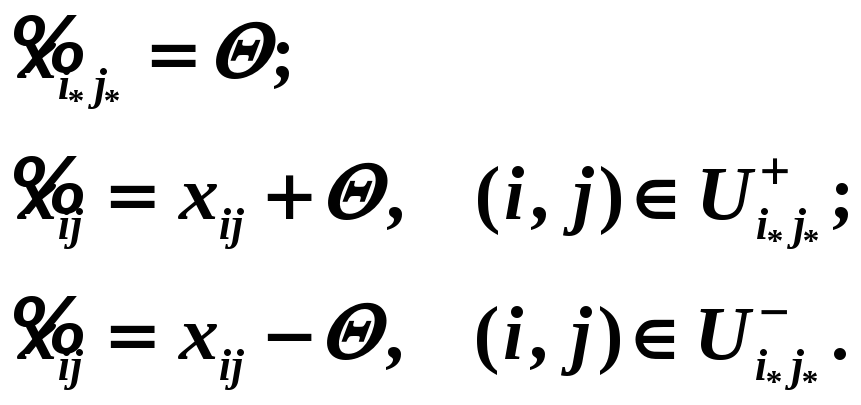
Формулы (1) отражают простой факт: циркуляция добавляется в клетках, помеченных знаком «+», и вычитается в клетках, помеченных знаком «-».
Уменьшение
транспортных затрат прямо пропорционально
циркуляции Θ
и составляет
величину
![]() ,
т.е. чем больше циркуляция, тем меньше
затраты. Однако циркуляция не может
быть скол угодно большой, поскольку
объемы поставок не могут быть
отрицательными. Действительно, в клетках
цикла, помеченных знаком «-», объемы
поставок уменьшаются на величину
циркуляции. При больших Θ
все они могут
стать отрицательными. Чтобы этого не
произошло, рассчитаем максимально
допустимую циркуляцию.
,
т.е. чем больше циркуляция, тем меньше
затраты. Однако циркуляция не может
быть скол угодно большой, поскольку
объемы поставок не могут быть
отрицательными. Действительно, в клетках
цикла, помеченных знаком «-», объемы
поставок уменьшаются на величину
циркуляции. При больших Θ
все они могут
стать отрицательными. Чтобы этого не
произошло, рассчитаем максимально
допустимую циркуляцию.
Так как отрицательные
объемы могут появиться только в клетках,
помеченных знаком «-», то в силу (3)
максимально допустимая циркуляция не
может быть больше минимального объема
поставки в этих клетках. Обозначим
максимально допустимую циркуляцию
через Θ0.
Тогда
![]() .
.
Таким образом, для вычисления максимально допустимой циркуляции необходимо найти минимальное из чисел xij, находящихся в клетках цикла, помеченных знаком «-».
12. Метод потенциалов решения транспортной задачи.
С каждой i-ой строкой
транспортной таблицы свяжем величину
Ui,
которую будем называть потенциалом
строки. Аналогично с каждым столбцом
свяжем величину Vj.
Для нахождения потенциалов составим
систему линейных алгебраических
уравнений:
![]()
В системе (1) (m+n-1)
уравнение и (n+m)
переменных потенциалов, поэтому система
(1) имеет бесконечное множество решений.
Нам нужно любое одно решение. Поэтому
один из потенциалов полагают
![]() ,
остальные потенциалы находят из системы.
Справедлива теорема: оценки небазисных
клеток связаны с потенциалами строк и
столбцов соотношением
,
остальные потенциалы находят из системы.
Справедлива теорема: оценки небазисных
клеток связаны с потенциалами строк и
столбцов соотношением
![]()
Поэтому суть метода потенциалов можно выразить двумя пунктами: для проверки условий оптимальности базисного плана перевозок
1) решаем систему;
2) находим оценки по формуле
Общая схема решения транспортной задачи не изменяется, остается такой же, как и распределительном методе
Полученные оценки заносим в правый верхний угол соответствующих клеток. Максимально допустимую циркуляция рассчитывается из минимальных объемов поставок, помеченных знаком минус.
13. Задача целочисленного линейного программирования: постановка, подходы к разработке методов.

Подходы:
1) Метод ветвей и границ
2) Метод отсечения основан на том, что вначале требование целочисленности отбрасывается, а затем вводятся дополнительные ограничения
