§2. Основные правила дифференцирования.
Дифференцирование основных элементарных функций
Основные правила дифференцирования
Пусть
C
–постоянная,
- функции, имеющие производные, тогда:
1.
2.
3.
4.
5.
Таблица производных
основных элементарных функций
-
1.
2.
3.
4.
5.
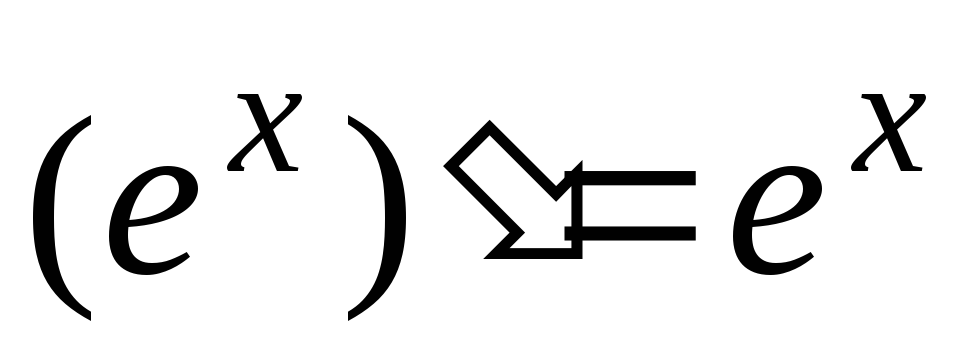
6.
7.
8.
9.
10.
11.
12.
13.
14.
Применяя формулы и правила дифференцирования, найдем производную функции:
Запишем данную функцию следующим образом:
Тогда
В качестве следующего примера найдем производную от функции
.
Для нахождения производной воспользуемся правилом нахождения производной от произведения двух функций:
И, наконец, рассмотрим еще один пример: нахождение производной частного от деления двух функций
.
Для нахождения производной воспользуемся пятым правилом из раздела «Основные правила дифференцирования».
Тогда
Найти производные следующих функций:
|
2.9. |
|
Ответ: 6(x1). |
|
2.10. |
|
Ответ:
|
|
2.11. |
|
Ответ: 2x(24x2+1). |
|
2.12. |
|
Ответ:
|
|
2.13. |
|
Ответ:
|
|
2.14. |
|
Ответ:
|
|
2.15. |
|
Ответ: |
|
2.16. |
|
Ответ:
|
|
2.17. |
|
Ответ:
|
|
2.18. |
|
Ответ:
|
|
2.19. |
|
Ответ:
|
|
2.20. |
|
Ответ:
|
|
2.21. |
|
Ответ:
|
|
2.22. |
|
Ответ:
|
|
2.23. |
|
Ответ:
|
|
2.24. |
|
Ответ:
|
|
2.25. |
|
Ответ:
|
|
2.26. |
|
Ответ:
|
|
2.27. |
|
Ответ:
|
|
2.28. |
|
Ответ:
|
|
2.29. |
|
Ответ:
|
|
2.30. |
|
Ответ:
|
|
2.31. |
|
Ответ:
|
|
2.32.
|
|
Ответ: |
|
2.33. |
|
Ответ:
|
|
2.34. |
|
Ответ:
|
|
2.35. |
|
Ответ:
|
|
2.36. |
|
Ответ: |
|
2.37. |
|
Ответ: 0. |
|
2.38. |
|
Ответ:
|
|
2.39. |
|
Ответ:
|
|
2.40. |
|
Ответ:
|
|
2.41. |
|
Ответ: |
|
2.42. |
|
Ответ: |
|
2.43. |
|
Ответ: |
|
2.44. |
|
Ответ:
|
|
2.45. |
|
Ответ: |
|
2.46. |
|
Ответ:
|
|
2.47. |
|
Ответ: |
|
2.48. |
|
Ответ: |
|
2.49. |
|
Ответ:
|
|
2.50. |
|
Ответ:
|
|
2.51. |
|
Ответ:
|
|
2.52. |
|
Ответ: |
|
2.53. |
|
Ответ:
|
|
2.54. |
|
Ответ:
|
|
2.55. |
|
Ответ:
|
|
2.56. |
|
Ответ:
|
|
2.57. |
|
Ответ:
|
|
2.58. |
|
Ответ:
|
|
2.59 |
|
Ответ:
|
|
2.60. |
|
Ответ:
|
|
2.61 |
|
Ответ:
|
|
2.62. |
|
Ответ: |
|
2.63 |
|
Ответ:
|
|
2.64. |
|
Ответ:
|
|
2.65. |
|
Ответ:
|
|
2.66 |
|
Ответ: |
|
2.67. |
|
Ответ:
|
|
2.68. |
|
Ответ:
|
|
2.69. |
|
Ответ:
|
|
2.70. |
|
Ответ:
|
|
2.71. |
|
Ответ:
|
|
2.72. |
|
Ответ: |
|
2.73. |
|
Ответ:
|
|
2.74.1 |
|
Ответ:
|
|
2.75. |
|
Ответ:
|
|
2.76. |
|
Ответ:
|
|
2.77. |
|
Ответ:
|
|
2.78. |
|
Ответ:
|
|
2.79.2 |
|
Ответ:
|
|
2.80.3 |
|
Ответ:
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.