§3. Однородные дифференциальные уравнения

Уравнения вида называются однородными уравнениями.

Однородное уравнение приводится к уравнению с разделяющимися переменными подстановкой y=Ux, где U- новая искомая функция. Дифференцируя равенство y=Ux, получим

.

Подставив выражения y и в уравнение, имеем

Это уже уравнение с разделяющимися переменными, найдя его общее решение и заменив U на , получим общее решение исходного уравнения.

Например.

1. Найти общее решение дифференциального уравнения

Запишем уравнение следующим образом:

.

Поделим числитель и знаменатель на х²:

, (*)

т.е. получим y как функцию от . Это означает, что данное уравнение однородное. Для решения этого уравнения введем новую функцию U=.

Тогда

y=Ux, .

Используя замену, запишем уравнение (*) в виде

Интегрируя последнее выражение, получим

Заменяя в полученном равенстве U отношением , окончательно имеем

.

Найти общее решение дифференциальных уравнений:

6.18.	.	6.19.	.
6.20.	.	6.21.	.

Найти частное решение дифференциальных уравнений:

6.22.
6.23
6.24.
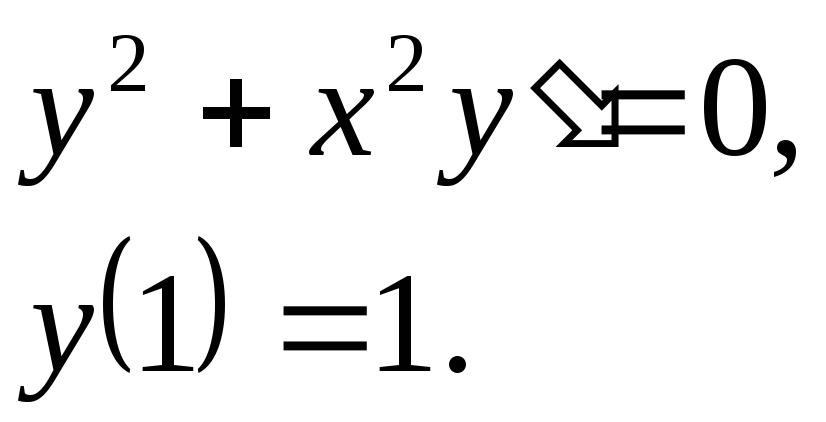
6.25

§4. Задачи на составление дифференциальных уравнений

Рассмотрим конкретный пример.

Скорость распада радия пропорциональна его имеющемуся количеству R. Найти закон распада радия, если известно, что через 1600 лет останется половина первоначального количества. Какой процент радия окажется распавшимся через 100 лет?

Решение. Пусть R- количество радия в момент времени t, а R₀- его первоначальное количество. Тогда скорость распада радия равна и является отрицательной величиной, т.к. R с течением времени убывает. Согласно условию задачи имеем: , где k>0 - коэффициент пропорциональности, подлежащий определению. Интегрируем полученное уравнение:

Осталось найти k и C. Для определения произвольной постоянной С воспользуемся начальным условием: R=R₀ в начальный момент времени t=0. Тогда R₀=С. Итак, закон распада радия имеет вид

Для нахождения k воспользуемся следующим условием: при t=1600. Отсюда

Таким образом, окончательно получаем

При t=100 имеем

Следовательно, через 100 лет распадается 4,2% первоначального запаса радия.

Решить задачи.

6.26 Тело за 10 мин охлаждается от 100 до 60С. Температура окружающего воздуха равна 20С. Считая скорость остывания тела пропорциональной разности температур тела и окружающего его воздуха, определить, за какое время тело остынет до 30С.

Указание. Пусть Т- температура тела в момент времени t. Тогда дифференциальный закон охлаждения тела имеет вид

.

6.27. Моторная лодка движется в спокойной воде со скоростью 1,5 м/с. Через 4с после выключения мотора ее скорость уменьшилась до 1 м/с. Считая, что сопротивление воды пропорционально скорости движения лодки, найти ее скорость через 50с после остановки мотора. Указание. Пусть V- скорость лодки после выключения мотора в момент времени t. Тогда зависимость между V и t имеет вид , где m- масса лодки.

6.28. Поглощение светового потока тонким слоем воды пропорционально толщине слоя и потоку, падающему на его поверхность. При прохождении через слой толщиной 2м поглощается 1/3 первоначального светового потока. Определить, какой процент первоначального светового потока дойдет до глубины 4м.

Указание. Пусть Q- световой поток, падающий на поверхность на глубине h. Тогда dQ = - kQdh.

29. Скорость тела V, брошенного вниз с начальной скоростью V_0, определяется равенством V=V₀+gt. Найти уравнение движения данного тела.

30. Скорость размножения некоторых бактерий пропорциональна начальному количеству бактерий. Найти зависимость изменения количества бактерий от времени.

31. Найти закон роста клеток с течением времени, если для пальчиковых клеток скорость роста 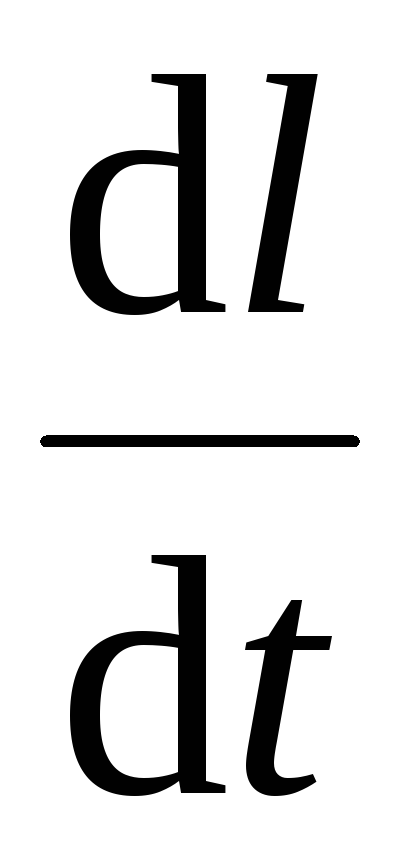пропорциональна длине клетки l в данный момент.

Указание. Пусть , где ,- постоянные, характеризующие процессы синтеза и распада.

29. По какому закону происходит разрушение клеток в звуковом поле, если скорость их разрушения пропорциональна начальному количеству N?

29. Скорость укорочения мышц описывается уравнением , где х₀- полное укорочение, х - укорочение в заданный момент. Найти закон сокращения мышц, если при t=0 величина укорочения была равна нулю.