
- •Асимптоты.
- •Из таблицы следует, что меняет знак при переходе через точку , но тогда по теореме 6 эта точка является абсциссой точки перегиба.
- •Знаки функций. , если и , если . Корни уравнения известны: и . Кривая знаков имеет вид (рис.12) рис.13
- •Строим график функции (рис.15)
- •Литература.
- •Предельная себестоимость характеризует себестоимость c прироста продукции q
- •II. Исследование функций с помощью производных.
Литература.
-
Г.М. Фихтенгольц. "Основы математического анализа" Т.1. Издательство "наука", М., 1964.
-
Н.С. Пикунов. "Дифференциальное и интегральное исчисления". Т.1. Издательство "Наука". М., 1976.
-
В. И. Смирнов. "Курс высшей математики". Т.1. Издательство "Наука". М., 1974.
-
М. С. Красс. "Математика для экономических специальностей". ИНФРА. М., 1998.
-
В. Е. Шнейдер и др. "Краткий курс высшей математики". Т.1. Издательство "Высшая школа". М., 1978.
Пример
2. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
Решение:
1. ОДЗ:
![]()
2. Функция общего вида.
3.
График функции пересекается с осью
![]()
![]() ,
когда
,
когда
![]() ,
т.е. в точке
,
т.е. в точке
![]() .
С осью
.
С осью
![]()
![]() график не пересекается, т.к.
график не пересекается, т.к.
![]() не входит в ОДЗ функции.
Внутри ОДЗ –
интервале
не входит в ОДЗ функции.
Внутри ОДЗ –
интервале
![]() - точек разрыва функции нет.
- точек разрыва функции нет.
4.
Так как
![]() всюду в ОДЗ, то знак функции определяется
знаком числителя. Так как
всюду в ОДЗ, то знак функции определяется
знаком числителя. Так как
![]() для
для
![]() и
и
![]() для
для
![]() ,
то функция отрицательна на интервале
,
то функция отрицательна на интервале
![]() .
.
5.
Для нахождения критических точек найдем
производную
![]() .
.
![]()
![]()
Производная
существует всюду в ОДЗ и равна нулю,
если
![]() ,
т.е. в точке
,
т.е. в точке
![]()
![]() ,
если
,
если
![]() или
или
![]()
![]() ,
если
,
если
![]() или
или
![]() .
.
Таким
образом, функция возрастает при
![]() и убывает при
и убывает при
![]() .
При переходе через точку
.
При переходе через точку
![]() производная меняет знак с "+" на
"-", следовательно,
производная меняет знак с "+" на
"-", следовательно,
![]() - точка, в которой функция достигает
максимума.
- точка, в которой функция достигает
максимума.
![]()
6.
Уравнение вертикальной асимптоты
![]() (ось
(ось
![]() ),
так как
),
так как
![]()
б) наклонные асимптоты:
![]()
![]()
![]() ,
,
![]()
![]() -
наклонная асимптота, т.е. наклонной
асимптотой является ось
-
наклонная асимптота, т.е. наклонной
асимптотой является ось
![]() .
.
-
Вычисляем
 .
.

![]() ,
если
,
если
![]() ,
т.е. при
,
т.е. при
![]()
![]() ,
т.е. кривая выпукла для
,
т.е. кривая выпукла для
![]() ,
,
![]() ,
т.е. кривая вогнута для
,
т.е. кривая вогнута для
![]() .
.
Так
как
![]() меняет знак при переходе через точку
меняет знак при переходе через точку
![]() ,
то эта точка есть абсцисса точки перегиба:
,
то эта точка есть абсцисса точки перегиба:
![]() .
.
 .
.
Для построения графика функции сводим в таблицу результаты исследования.
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
+ |
1 |
+ |
0 |
- |
|
- |
|
|
- |
-3 |
- |
|
- |
0 |
+ |

Рис.10.
Пример
3. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
-
ОДЗ определяем из условия
 ,
откуда
,
откуда
 ,
, т.е.
ОДЗ является вся ось
т.е.
ОДЗ является вся ось
 кроме точек
кроме точек
 .
. -
Функция
 является периодической, четной (т.к.
функция
является периодической, четной (т.к.
функция
 периодическая и четная). Период равен
периодическая и четная). Период равен
 .
График функции симметричен, поэтому
для его построения достаточно исследовать
функцию на отрезке
.
График функции симметричен, поэтому
для его построения достаточно исследовать
функцию на отрезке
 ,
и затем периодически продлить его на
всю ось
,
и затем периодически продлить его на
всю ось
 .
. -
График функции пересекается с осью

 в точке
в точке
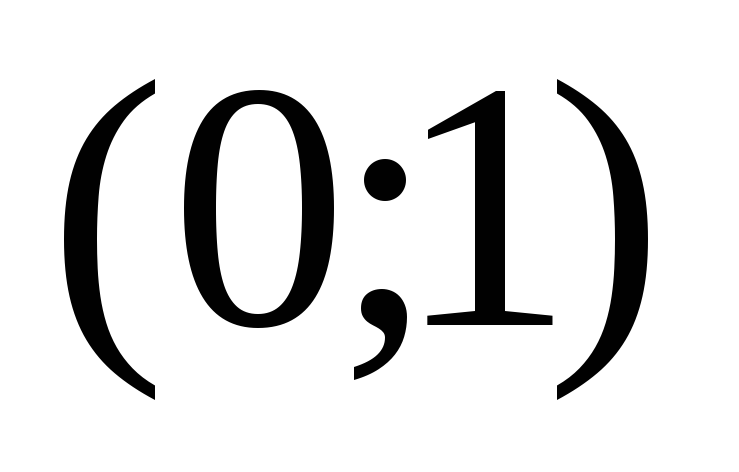 .
С осью
.
С осью

 график ни где не пересекается, так как
ни при каком конкретном
график ни где не пересекается, так как
ни при каком конкретном

 не равен нулю. Точки разрыва функции
не равен нулю. Точки разрыва функции
 - точки разрыва второго рода.
- точки разрыва второго рода.
На
рассматриваемом отрезке
![]()
![]() ,
а
,
а
 и
и
 ,
а
,
а
 .
.
-
Функция положительна при
 и при
и при
 и отрицательна при
и отрицательна при
 .
. -
Для нахождения экстремума вычислим
 и
и

 .
.
Суть
понятия предела функции f(x)
при xx0
в том, что
если он существует и равен числу b,
то отличие функции от предела |b-f(x)|
можно сделать сколь угодно малым,
приближая x
к x0.
Сколь угодно малым означает, что это
отличие будет меньше любого наперед
заданного числа
![]() >0,
как бы мало
>0,
как бы мало
![]() не было. Иными
словами: если всегда найдется x
достаточно близкое к x0,
при котором |b-f(x)|<
не было. Иными
словами: если всегда найдется x
достаточно близкое к x0,
при котором |b-f(x)|<
![]() ,
то число b
есть предел функции f(x)
при xx0.
,
то число b
есть предел функции f(x)
при xx0.
Строгое понятие предела “на языке “ дает определение 1.
Пусть функция f (x) определена в некоторой окрестности точки x = x0, кроме, быть может, самой точки x0.
Число
b
называется пределом функции f(x)
при xx0,
если для любого числа
![]() >0
как бы мало оно ни было, найдется такое
число
>0
как бы мало оно ни было, найдется такое
число
![]() >0,
что для всех x,
удовлетворяющих условию 0<|b-f(x)|<
>0,
что для всех x,
удовлетворяющих условию 0<|b-f(x)|<
![]() , будет выполняться неравенство |b-f(x)|<
, будет выполняться неравенство |b-f(x)|<
![]() .
.
В этом случае пишут:
![]() f
(x)=b
(1)
f
(x)=b
(1)
Из определения следует, что в самой точке x0, функция f(x) может быть не определена, то есть при образовании предела функции предельное значение x0 переменной x не учитывается. Это делает возможным сокращение под знаком предела при xx0 множителей вида (xx0), стоящих в числителе и в знаменателе, что удобно при вычислении пределов.
Особый интерес представляет случай, когда предел функции f(x) при xx0 совпадает со значением функции в точке x0, т.е. когда
![]() f
(x)
f
(x0)
(2)
f
(x)
f
(x0)
(2)
В этом случае говорят, что функция f(x) непрерывна в точке x0; если же соотношение (2) нарушено, то говорят, что в точке x0 функция f(x) имеет разрыв.
Понятие производной базируется на понятии предела.
Определение
2. Производной функции y
= f(x)
в точке x0
называется
предел отношения приращения функции в
этой точке
![]() y
к приращению аргумента
y
к приращению аргумента
![]() x
при стремлении приращения аргумента к
нулю любым способом.
x
при стремлении приращения аргумента к
нулю любым способом.
Обозначается
производная одним из символов y’(x0),
f’(x0),
![]() ;
таким образом, можно записать
;
таким образом, можно записать
![]() (3)
(3)
В общем случае производная является функцией и от неё так же можно находить производную, которую называют производной второго порядка (второй производной).
Вторую производную обозначают символами:
![]() ,
,
![]() ;
;
![]() (4)
(4)
От второй производной можно находить третью производную и т.д.
К пределу (3) приводят многочисленные задачи в различных областях науки. В связи с этим существуют: механический смысл производной, геометрический смысл производной и т.п.
В экономике производная применяется для выражения предельных показателей: себестоимости и эластичности.
Поскольку себестоимость C произведенной продукции зависит от ее объема Q, то:
C = f (Q) (5)

