3. Оценка границ погрешностей косвенного измерения.
Пусть косвенное измерение искомой величины Y находятся по результатам прямых измерений x1, x2, …, xn при помощи известной зависимости
Y = f(x1, x2, …, xn) (1).
Наиболее вероятным значением Y следует считать значение <y>, которое получиться, если в формулу (1) подставить средние значения аргументов x1, x2, …, xn:
Y = <y> = f(<x1>, <x2>, …, <xn>).
Если x1, x2, …, xn являются независимыми друг от друга, то доверительная граница относительной погрешности γ измерения величины Y оценивается по формуле:
.
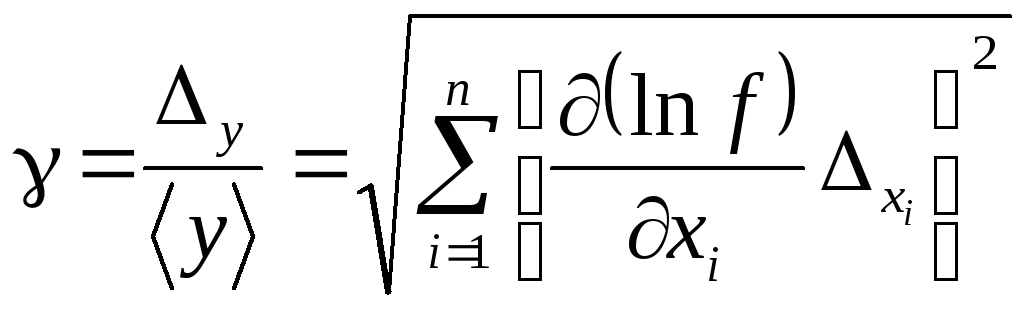Только после этого вычисляют границу абсолютной погрешности результата измерения величины Y:
.
Окончательный результат косвенного измерения записывают в виде:
Y = <y> ±ΔY , P = 0,95.
Пример.
В лабораторной работе №1 плотность ρ твердого тела цилиндрической формы определяется согласно формуле
(2),
где m – масса цилиндра, d – диаметр цилиндра, h – высота цилиндра.
Прологарифмируем выражение (2):
.
Найдем частные производные от этого выражения по всем переменным:
; 
;
; 
.
Запишем формулу для относительной погрешности результата измерения плотности:
.
Найдем границу абсолютной погрешности результата измерения плотности:
.
Окончательный результат запишем в виде:
ρ = <ρ> ±Δρ кг/м3, P = 0,95.
В заключение отметим, что окончательные результаты оценки погрешностей записываются с точностью до одной значащей цифры, а все промежуточные вычисления величин θx, S<x>, εx и Δx необходимо проводить с точностью не более двух значащих цифр.
1 Карл Гаусс (1777-1855), немецкий математик, астроном и физик
2Уильям Сили Госсет (1876-1937), английский статистик, работал под псевдонимом «Стьюдент».