Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции

Понятие предела является одним из основных в математическом анализе. В элементарной математике с помощью предельных переходов определяется длина окружности, объемы цилиндра и конуса, сумма членов бесконечно убывающей геометрической прогрессии.

2.3.1. Предел переменной величины.

Если значения переменной величины в процессе её изменения как угодно близко приближаются к некоторому числу , то говорят, что переменная величина стремится к или предел переменной величины равен , обозначают или .

Различные переменные величины к своему предельному значению могут стремиться по разному: убывая справа, возрастая слева, колеблясь около своего предельного значения.

Пример. Рассмотрим математический маятник (см. рис.2.3.1). – угол отклонения маятника от положения равновесия – переменная величина.

Маятник стремится к положению равновесия, это значит, что угол отклонения, изменяясь со временем, колеблется около своего предельного значения, стремясь к нулю, т.е. .

О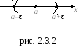пределение. Пусть – некоторое значение переменной величины и – сколь угодно малое положительное число. Все точки интервала (кроме самой точки ), удовлетворяющие неравенству , образуют –окрестность точки (см. рис.2.3.2).

Определение. Пределом переменной величины называется число , если для любого сколь угодно малого числа , найдется такое значение переменной величины , что для всех значений переменной величины, больших , выполняется неравенство .

Иначе говоря, если – предел переменной величины , то все значения переменной величины , большие , попадут в –окрестность точки .

Аналогично можно дать определение предела для числовой последовательности (функции где ).

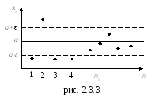Определение. Число называется пределом последовательности , если для любого сколь угодно малого числа найдется такой номер , что для всех номеров выполняется неравенство .

Иначе говоря, если , то все точки , начиная с , попадают в полосу, ограниченную прямыми и (см. рис. 2.3.3).

Пример. Используя определение предела последовательности, доказать, что .

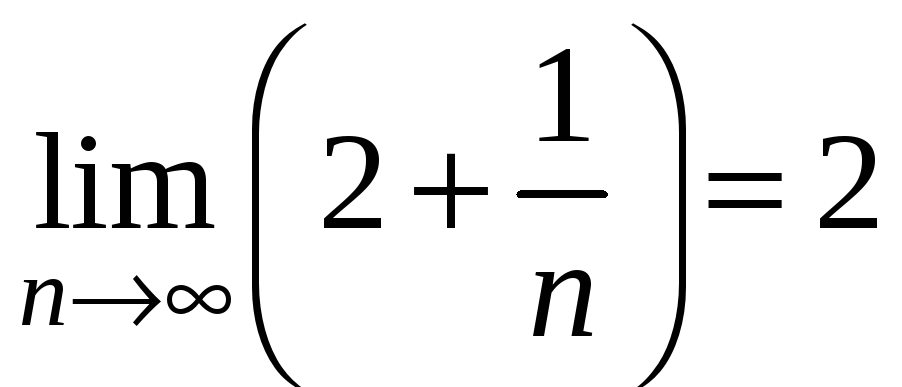Решение:

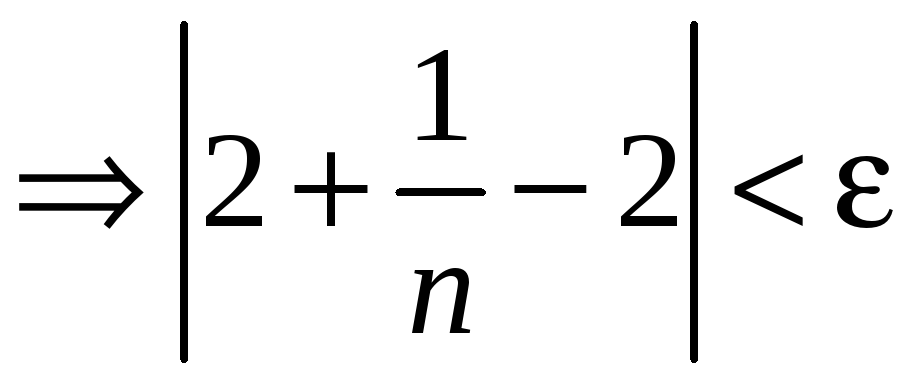, По определению, число 2 будет пределом данной последовательности , если для любого найдется , такое что для всех , т. е. , т.е. для всех 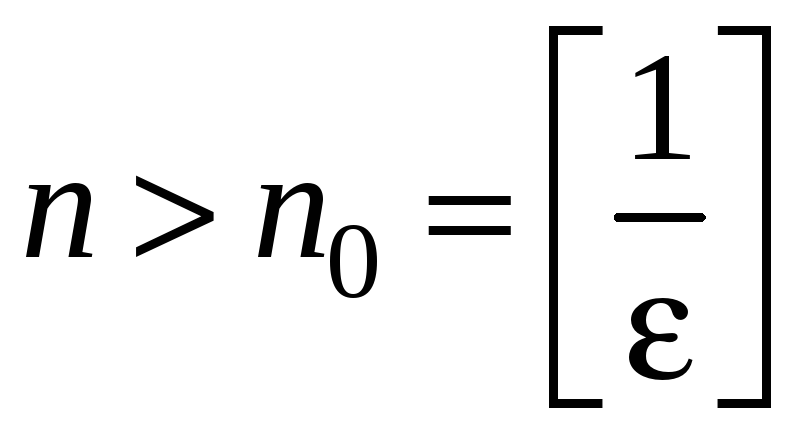, где целая часть числа . Пусть , тогда . Таким образом существует , такое что для всех . Ч. и т. д. Значит .

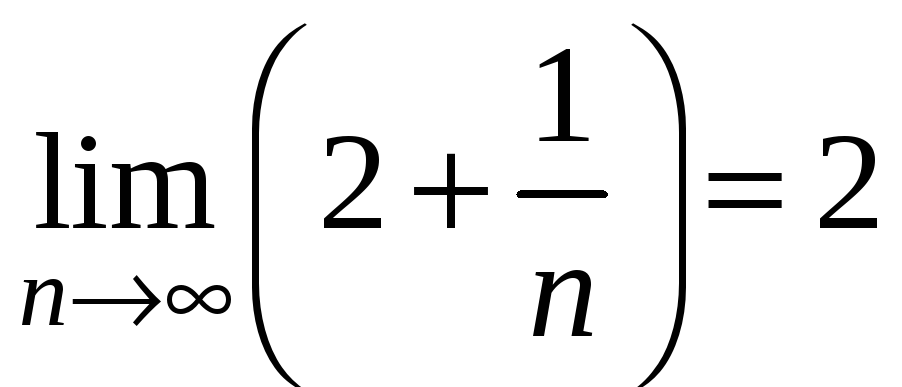2.3.2. Предел функции

Рассмотрим – функцию одной переменной, определенную в – окрестности точки .

Определение. Число называется пределом функции в точке (или при ), если для любого наперед заданного сколь угодно малого , найдется такое число , что для всех , удовлетворяющих условию , выполняется неравенство .

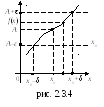Иначе говоря, если , то точки графика функции с абсциссами из – окрестности точки и соответствующими им ординатами из ‑окрестности точки должны лежать в полосе, ограниченной двумя прямыми и (см. рис. 2.3.4).

Примеры.

1. Доказать, что .

Решение: , если для любого сколь угодно малого , найдется такое число , что для всех , удовлетворяющих условию , выполняется неравенство , т. е. , тогда .

Если , то и для всех удовлетворяющих неравенству , а значит . Ч. и т. д.

2. Доказать, что если , то .

Решение: Для любого можно взять любое , тогда при , имеем . Следовательно, .

В связи с тем, что для функции одной переменной можно приближаться к по двум направлениям (слева и справа), существуют понятия левостороннего и правостороннего пределов.

Определение. Число называется левосторонним пределом функции в точке , если для любого сколь угодно малого наперед заданного числа , найдется такое число , что при выполняется неравенство .

Иначе говоря, если слева (оставаясь меньше ), то предел функции – левосторонний, записывается в виде .

Определение. Число называется правосторонним пределом функции в точке , если для любого сколь угодно малого наперед заданного числа , найдется такое число , что при выполняется неравенство .

Иначе говоря, если справа (оставаясь больше ), то предел функции – правосторонний, записывается в виде .

Пределы функции слева и справа называются односторонними пределами.

Имеют место теоремы о существовании предела функции в точке.

Теорема 1. Если существует , то существуют односторонние пределы , , которые равны между собой и равны пределу функции в точке , т. е. .

Теорема 2 (обратная). Если существуют равные межу собой односторонние пределы, т. е. , то существует .

Если же, , то не существует.

Пусть функция определена на интервале .

Определение. Число называется пределом функции при , если для любого наперед заданного сколь угодно малого числа найдется число такое, что для всех , удовлетворяющих условию выполняется неравенство .

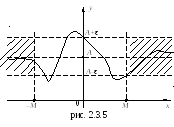И наче говоря, если , то для всех или соответствующие значения функции попадают в –окрестность точки , т.е. точки графика лежат в полосе, ограниченной прямыми и (см. рис. 2.3.5).

Если , то пишут , если , то пишут .

Рассмотрим – функцию двух переменных, определенную на некоторой области .

Определение. Пусть точка и – некоторое сколь угодно малое положительное число. Совокупность всех точек , лежащих внутри окружности с центром в точке и радиусом (за исключением самой точки , т.е. ), удовлетворяющих неравенству , образуют –окрестность точки (см. рис.2.3.6).

О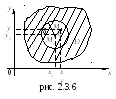пределение. Число называется пределом функции двух переменных в точке , если для любого малого числа найдется число , такое, что для всех точек из –окрестности точки выполняется неравенство .

Обобщим понятия предела в точке для функции любого числа переменных.

Рассмотрим функцию переменных , которая определена в некоторой области – мерного пространства. Пусть точка ; – окрестность этой точки будет представлять совокупность точек, расположенных внутри -мерного шара с центром в точке и радиусом , координаты которых удовлетворяют неравенству: , где .

Определение. Число называется пределом функции в точке , если для любого сколь угодно малого числа найдется число , такое, что для всех точек –окрестности точки выполняется неравенство , где .

Понятия предела в точке для функций одной, двух и большего числа переменных можно получить из последнего определения как частные случаи при , , и т. д.

Анализируя это определение предела функции предела функции в точке , отметим его особенности:

– в определении не рассматривается значение функции в точке , поэтому функция может быть не определена в этой точке, но иметь в ней предел;

– о существовании предела функции в этой точке можно говорить только в том случае, если при приближении к этой точке по различным направлениям значения функции стремится к одному и тому же числу. В частности, для функции существование предела в точке равносильно его существованию при стремлении к по любым направлениям (например, по прямым , параболам , и т.д.), а для функции можно устремляться к точке по оси слева или справа;

– определение предела не дает способов его вычисления , оно дает возможность доказать его существование.