2.4.2. Признаки существования пределов

Не всякая функция, даже ограниченная, имеет предел. Например, функция при предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования пределов.

Теорема 5. (О пределе промежуточной функции)

Если функция заключена между двумя функциями и , стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е. если , и , то

.

Доказательство:

Так как и , то для любого существуют две окрестности и точки , для всех точек которых соответственно выполняются неравенства и .

Пусть –меньшее из чисел и . Тогда в –окрестности точки выполняются оба неравенства.

По условию , тогда .

Получаем или . Это значит, что , т.е. . Ч. и т. д.

Теорема 6. (О пределе монотонной функции)

Если функция монотонна и ограничена при или при , то существует соответственно её левый предел или её правый предел .

Теорема 7. (Вейерштрасса)

Ограниченная монотонная последовательность , , имеет предел.

Заметим, что теорему 7 можно считать следствием теоремы 6.

Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них

2.5.1. Первый замечательный предел

Первым замечательным пределом называется предел вида

(2.5.1)

Доказательство:

Для доказательства формулы (2.5.1) рассмотрим круг радиуса с центром в точке .

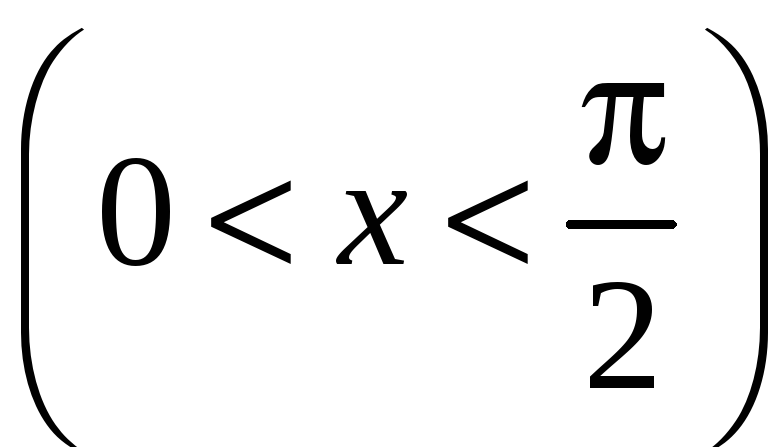Пусть – радиус вектор точки , лежащей на окружности радиуса с центром в точке , образующий угол с осью , дуга численно равна центральному углу (см. рис.2.5.1).

На рис.2.5.1 видно, что площадь треугольника меньше площади сектора , которая в свою очередь меньше площади прямоугольного треугольника , т. е.

.

Так как , то имеем

.

Разделим все части полученного двойного неравенства на , получаем или .

Так как функции и четные (см. п.2.2.4), то полученные неравенства справедливы и при . и .

Тогда по признаку (о пределе промежуточной функции) существования предела (см. теорему 5 п.2.4.2) . Ч. и т. д.

Примеры.

1.

2.

.

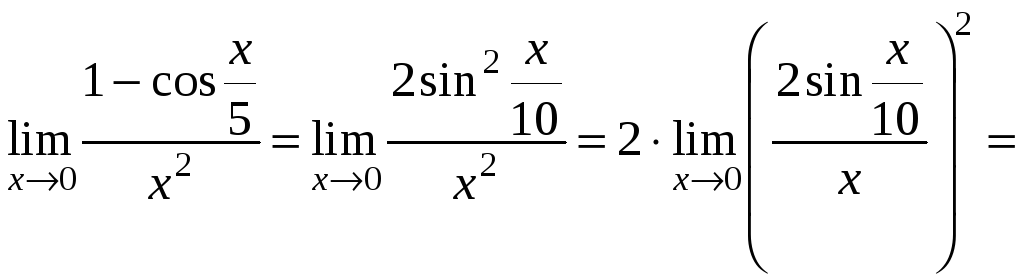
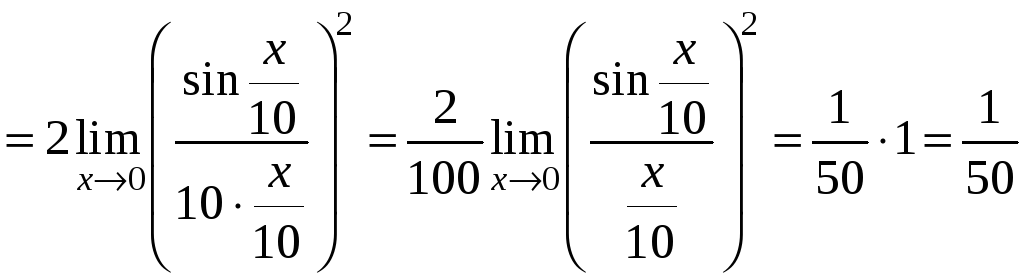2.5.2. Второй замечательный предел

Вторым замечательным пределом называется предел вида

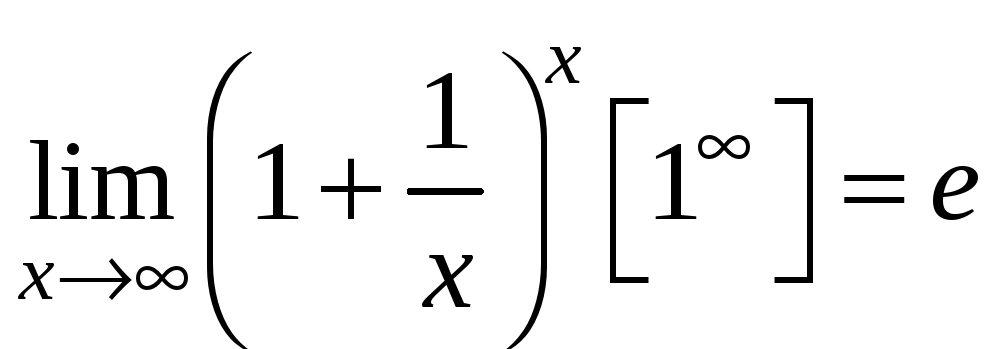(2.5.2)

или

(2.5.3)

Доказательство:

Для доказательства формулы (2.5.2) рассмотрим прежде предел числовой последовательности , при .

Докажем, что эта последовательность удовлетворяет теореме Вейерштрасса (см. теорема 7 п. 2.2.4), т.е. имеет предел и он равен , иначе говоря

. (2.5.4)

Докажем, что последовательность 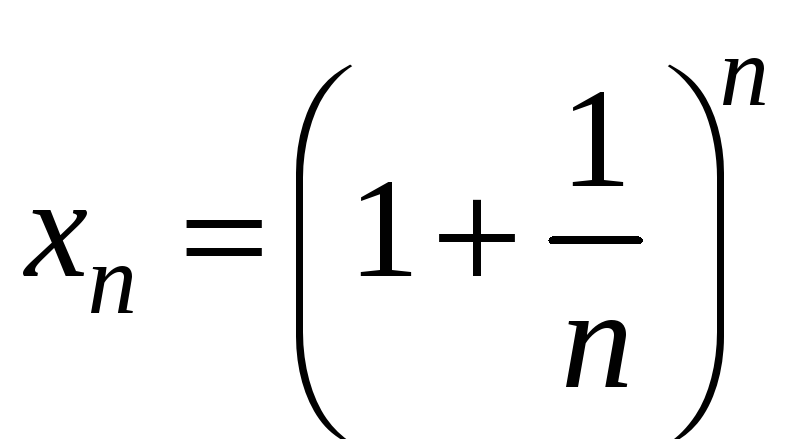возрастающая, а значит монотонная, и что она ограничена.

По формуле бинома Ньютона

.

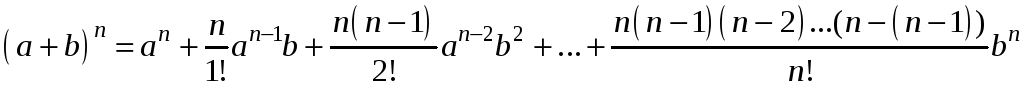Полагая , , получим

Т. е. (2.5.5)

Из последнего равенства следует, что с увеличением число положительных слагаемых увеличивается, число убывает, поэтому величины , , возрастают, поэтому последовательность – возрастающая, при этом

. (2.5.6)

Покажем, что последовательность – ограничена. Заменим каждую скобку в правой части равенства (2.5.5) на единицу; правая часть увеличится, получим неравенство

.

Усилим полученное неравенство, заменив числа 3, 4, 5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдем по формуле суммы членов бесконечно убывающей геометрической прогрессии с и :

.

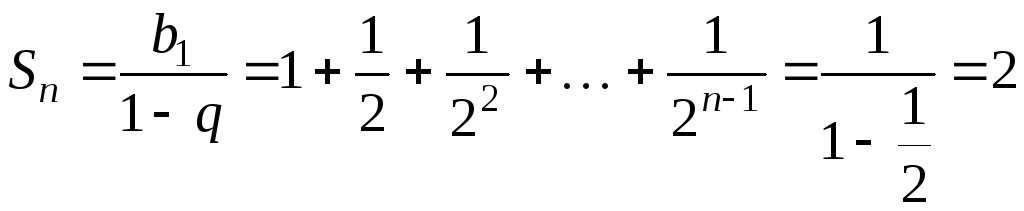Поэтому

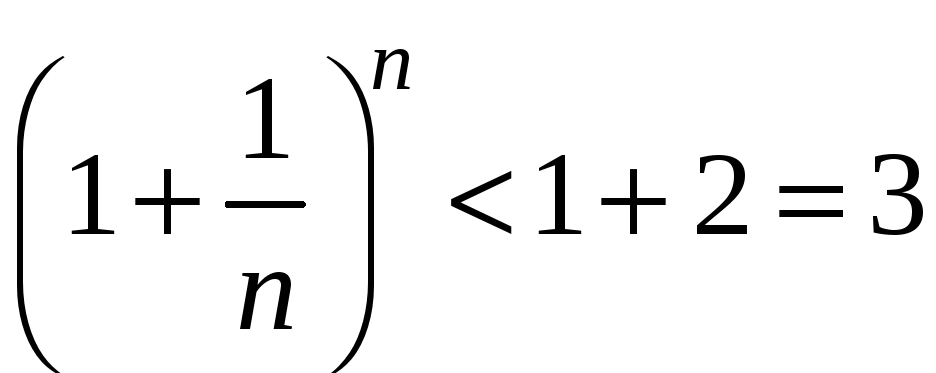. (2.5.7)

Итак, последовательность – ограничена, при этом для выполняются неравенства (2.5.6) и (2.5.7):

.

Следовательно, на основании теоремы Вейерштрасса последовательность , , имеет предел, обозначенный : .

Ч. и т. д.

Число называется неперовым числом. Число иррациональное, его приближенное значение равно . Число принято за основание натурального логарифма.

Докажем теперь что к числу стремится и функция при : .

1. Пусть .

Каждое значение заключено между двумя положительными целыми числами: , где – это целая часть числа . Отсюда следует , , поэтому

.

Если , то . Поэтому согласно формуле (2.5.4), имеем:

.

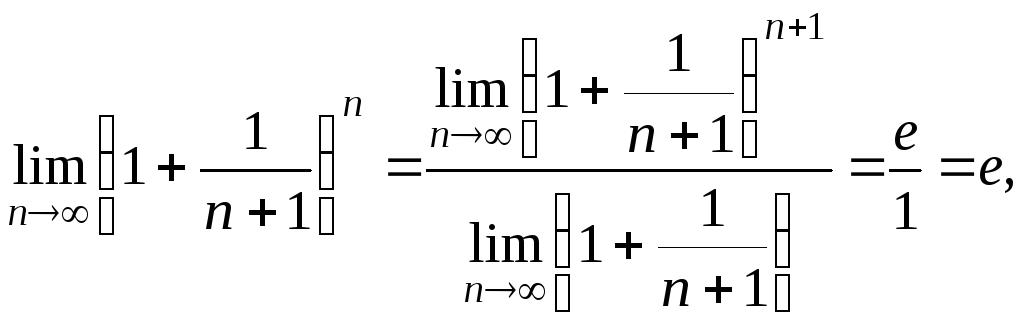
По признаку (о пределе промежуточной функции) существования пределов (см. теорему 5 п. 2.4.2)

(2.5.8)

2. Пусть .

Сделаем подстановку , тогда и при , . Получаем

т. е.

(2.5.9)

Из равенств (2.5.8) и (2.5.9) вытекает равенство (2.5.2), т.е.

. Ч. и т. д.

Докажем равенство (2.5.3) : выполним подстановку , тогда и при , . Получаем . Ч.и т. д.

Примеры.

1. , т.к. , , то окончательно получим

2.

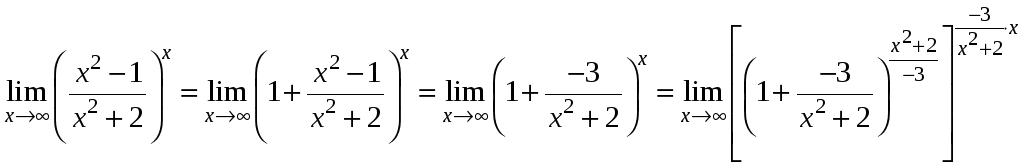
т.к. то окончательно получим

3.

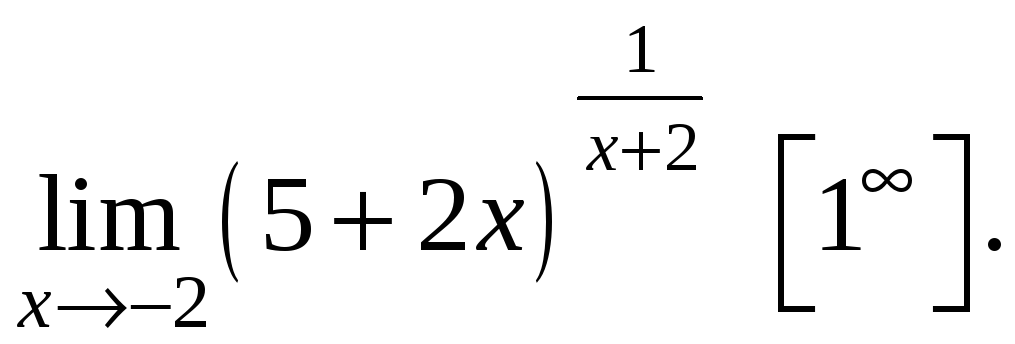
Выполним подстановку , тогда и при , . Получаем .

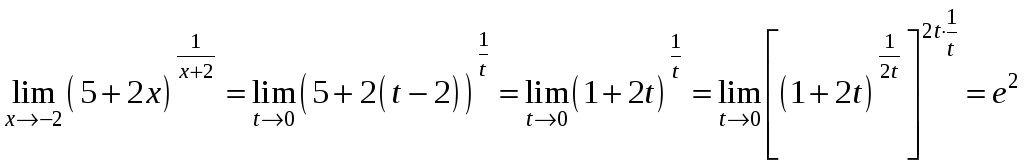Используя прием, рассмотренный в приведенных выше примерах можно найти множество других пределов.

При вычислении пределов вида где возможны варианты.

1. Если то .

2. Если то .