2.2.4. Основные свойства функции

Изучить заданную функцию – это значит охарактеризовать ход её изменения при изменении независимой переменной.

Функции многих переменных, с которыми приходится иметь дело в инженерной практике, по своим свойствам, за исключением некоторых, мало отличаются от функций одной переменной. Поэтому рассмотрим основные характеристики поведения функции на примере функции одной переменной.

Определение. Нулем функции называют такое значение , при котором .

В интервале положительного знака функции график расположен выше оси , в интервале отрицательного знака – ниже оси , в нуле функции график пересекает ось .

Пример. Найти точки пересечения графика функции с осью .

Решение: Ордината точки пересечения графика функции с осью равна нулю, т.е. . Значит абсцисса точки пересечения – есть нуль функции. Используя определение, получаем:

;

,

.

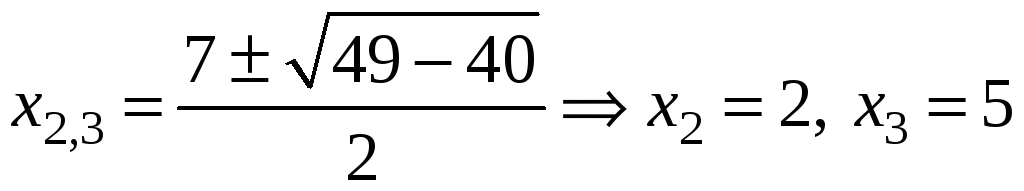Т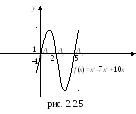аким образом, нули функции: а точки пересечения графика функции с осью : , , (см. рис.2.2.5).

Определение. Промежутком, симметричным относительно начала координат, называется промежуток, которому вместе со значением принадлежит противоположное ему значение: .

Определение. Функция , заданная на симметричном относительно начала координат промежутке, называется четной, если для любого значения из этого промежутка выполняется равенство .

Г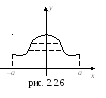рафик четной функции симметричен относительно оси (см. рис. 2.2.6).

О

y

пределение. Функция , заданная на симметричном относительно начала координат промежутке, называется нечетной, если для любого значения из этого промежутка выполняется равенство .

Г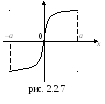рафик нечетной функции симметричен относительно начала координат (см. рис.2.2.7).

Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).

Произведение двух четных или двух нечетных функций есть функция четная, а произведение четной функции на нечетную – нечетная функция.

Пример. Функция – четная, так как в области определения выполняется равенство . А функция – ни четная, ни нечетная, так как на всей числовой оси и , где .

Определение. Функция называется периодической, если существует число такое, что для любого значения из области определения функции выполняется равенство , где – наименьший положительный период.

Если – наименьший положительный период функции, то число , где – также является периодом функции.

Пример. Наименьшим положительным периодом функциЙ и является число , а для функций и это число .

И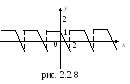з определения периодической функции следует, что её график будет «повторять» себя через промежуток равный по длине наименьшему положительному периоду . Поэтому достаточно построить график такой функции на любом промежутке вида . Смещая построенный график вдоль оси на отрезке длины , получим график функции .

Пример. График функции

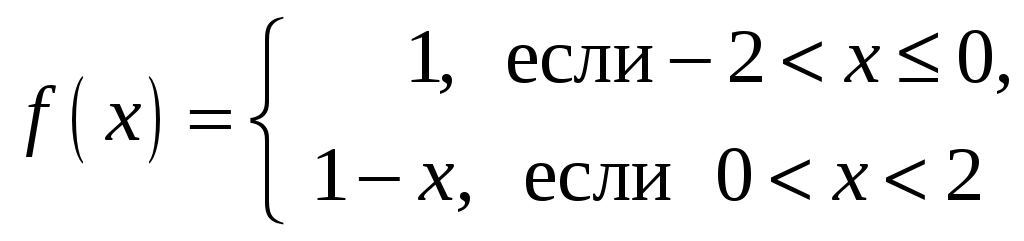
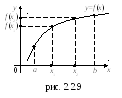– периодической, с наименьшим положительным периодом (см. рис.2.2.8).

Определение. Функция называется возрастающей на некотором интервале, если большим значениям аргумента соответствуют большие значения функции, т.е. если , то (см. рис. 2.2.9).

Определение. Функция называется убывающей на некотором интервале, если большим значениям аргумента соответствуют меньшие значения функции, т.е. если , то (см. рис.2.2.10).

Возрастающие и убывающие функции называются монотонными функциями. Интервал, на котором функция возрастает (убывает) называется интервалом возрастания (убывания) функции или интервалом монотонности.

О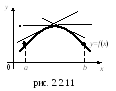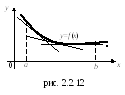пределение. График функции называется выпуклым (вогнутым) на некотором интервале, если касательная, проведенная к графику функции в любой точке с абсциссой из этого интервала, расположена выше (ниже) графика функции (см. рис. 2.2.11, 2.2.12).

Определение. Функция называется ограниченной, если существует такое число , что для всех выполняется неравенство .

График ограниченной функции лежит между прямыми и .

Определение. Значение функции, большее (меньшее) всех других её значений в некотором интервале, называется наибольшим (наименьшим) значением функции в этом интервале.

Ограниченная на некотором отрезке функция принимает на этом отрезке свое наибольшее и наименьшее значения.

Определение. Пусть задана функция с областью определения и областью значений . Если каждому значению соответствует единственное значение , то определена функция , обратная к функции , с областью определения и областью значений .

Про функции и говорят, что они являются взаимно обратными. Чтобы найти функцию достаточно решить уравнение относительно (если это возможно).

Примеры.

1. Для функции обратной является функция .

2. Для функции на интервале обратная функция существует и имеет вид , а на интервале не существует, так как одному значению соответствует два значения .

Если необходимо построить графики взаимно обратных функций так, чтобы ось была осью аргумента, надо обозначить аргумент в обратной функции через , а функцию через , т.е. функция примет вид .

График обратной функции симметричен с графиком функции относительно биссектрисы первого и третьего координатных углов (см. рис.2.2.13).

Г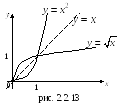еометрически ясно, что только монотонная функция имеет обратную, однозначную функцию.

Определение. Пусть функция определена на множестве , а функция на множестве , причем для любого , соответствующее значение . Тогда на множестве определена функция , которая называется сложной функцией от (или суперпозицией заданных функций, или функцией от функции).

Переменную называют промежуточным аргументом сложной функции.

Пример. Функция есть суперпозиция двух функций и .

Сложная функция может иметь несколько промежуточных аргументов.

Пример. Функция является сложной функцией двух промежуточных аргументов , где , а промежуточные аргументы: и .