2.1.2. Множество действительных чисел

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

– – множество натуральных чисел;

– – множество целых неотрицательных чисел;

– – множество целых чисел;

– – множество рациональных чисел.

Определение. Множество всех бесконечных десятичных дробей называется множеством действительных чисел и обозначается , а каждая такая дробь называется действительным числом.

Множество всех рациональных чисел является подмножеством множества , т. е. .

Действительные числа, не являющиеся рациональными, называются иррациональными . Иррациональные числа изображаются бесконечными непериодическими десятичными дробями.

Г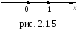еометрически множество действительных чисел изображается точками числовой прямой (или числовой оси) (см. рис. 2.1.5), т.е. прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба.

Между множеством действительных чисел и точками числовой прямой существует взаимно однозначное соответствие, т. е. Каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой – определенное действительное число. Поэтому часто вместо «число » говорят «точка ».

Пусть и – действительные числа, причем , тогда числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:

– – отрезок (сегмент, замкнутый промежуток);

– – интервал (открытый промежуток);

–, – полуоткрытые интервалы (или полуоткрытые отрезки);

– бесконечные интервалы (промежутки):

, , ,

, .

Числа и называются соответственно левым и правым концами этих промежутков. Символы и не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси от начала влево и вправо.

О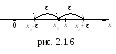 пределение. Пусть – любое действительное число (точка на числовой прямой). Окрестностью точки называется любой интервал , содержащий точку . В частности, интервал , где называется –окрестностью точки . Число называется центром, а число –радиусом (см. рис. 2.1.6).

Если , то выполняется неравенство , или, что то же . Выполнение последнего неравенства означает попадание точки в -окрестность точки (см. рис.2.1.6).

Упорядоченные пары действительных чисел можно изображать точками координатной плоскости.

Под координатной плоскостью будем понимать плоскость с заданными на ней двумя взаимно перпендикулярными координатными осями (или числовыми прямыми). Поэтому множество упорядоченных пар действительных чисел будем называть числовой плоскостью, а любую числовую пару – точкой числовой плоскости.

Числовую плоскость будем обозначать . На числовой плоскости можно применять геометрическую терминологию. Например, множество пар или точек, координаты которых удовлетворяют уравнению , есть прямая, а именно биссектриса первого и третьего координатных углов.

Множество точек , координаты которых удовлетворяют уравнению , есть кубическая парабола.

Пример. Указать множество точек плоскости, заданных условием .

Р ешение: Искомое множество показано штриховкой на рис.2.1.7.