
- •Раздел 2. Дифференциальное исчисление 138
- •Раздел 2. Дифференциальное исчисление лекция 2.1. Множества. Операции над множествами. Отображение множеств. Мощность множества. Множество действительных чисел
- •2.1.1. Множества. Операции над множествами. Отображение множеств
- •Свойства.
- •2.1.2. Множество действительных чисел
- •Лекция 2.2. Переменная величина. Функция одной и нескольких переменных. Способы задания. Основные элементарные функции, их свойства и графики
- •2.2.1. Переменная величина
- •2.2.2. Функция одной и нескольких переменных
- •2.2.3. Способы задания функции
- •2.2.4. Основные свойства функции
- •2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики
- •Основные элементарные функции
- •Лекция 2.3. Предел переменной величины. Предел последовательности. Предел функции в точке. Бесконечно малые и бесконечно большие функции
- •2.3.1. Предел переменной величины.
- •2.3.2. Предел функции
- •2.3.3.Бесконечно малая и бесконечно большая функции, их свойства
- •Лекция 2.4. Теоремы о пределах и их применение. Признаки существования пределов
- •2.4.1. Теоремы о пределах
- •2.4.2. Признаки существования пределов
- •Лекция 2.5. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •2.5.1. Первый замечательный предел
- •2.5.2. Второй замечательный предел
- •2.5.3. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые и теоремы о них
- •Лекция 2.6. Приращение функции одной и двух переменных. Непрерывность функции одной и двух переменных. Точки разрыва
- •2.6.1. Приращение функции одной и двух переменных
- •2.6.2. Непрерывность функции одной и двух переменных
- •2.6.3. Точки разрыва
2.6.3. Точки разрыва
Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции, а сама функция – разрывной в этой точке.
Если
![]() – точка разрыва функции
– точка разрыва функции
![]() ,
то в ней не выполняется по крайней мере
одно из условий определения 2 непрерывности
функции.
,
то в ней не выполняется по крайней мере
одно из условий определения 2 непрерывности
функции.
О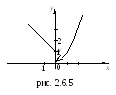 пределение.
Точка
пределение.
Точка
![]() называется точкой
разрыва I–го
рода
функции
называется точкой
разрыва I–го
рода
функции
![]() ,
если односторонние пределы функции в
этой точке существуют, конечны, но не
равны между собой, т.е.
,
если односторонние пределы функции в
этой точке существуют, конечны, но не
равны между собой, т.е.
![]() ,
,
![]() и
и
![]() .
.
Пример.
Функция
![]() задана аналитическими выражениями двух
функций
задана аналитическими выражениями двух
функций
![]() и
и
![]() ,
которые непрерывны соответственно на
интервалах
,
которые непрерывны соответственно на
интервалах
![]() и
и
![]() (см. рис. 2.6.5).
(см. рис. 2.6.5).
![]() – точка разрыва
I-го
рода, так как
– точка разрыва
I-го
рода, так как
![]() ,
,
![]() ,
,
![]() ,
т.е. односторонние пределы функции
,
т.е. односторонние пределы функции
![]() в точке
в точке
![]() существуют, конечны, но не равны между
собой.
существуют, конечны, но не равны между
собой.
Определение.
Точка
![]() называется точкой
устранимого разрыва
функции
называется точкой
устранимого разрыва
функции
![]() ,
если односторонние пределы функции в
этой точке существуют, конечны, равны
между собой, но не равны значению функции
в этой точке, т.е.
,
если односторонние пределы функции в
этой точке существуют, конечны, равны
между собой, но не равны значению функции
в этой точке, т.е.![]() и
и
![]() .
.
П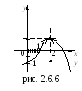 ример.
Для функции
ример.
Для функции
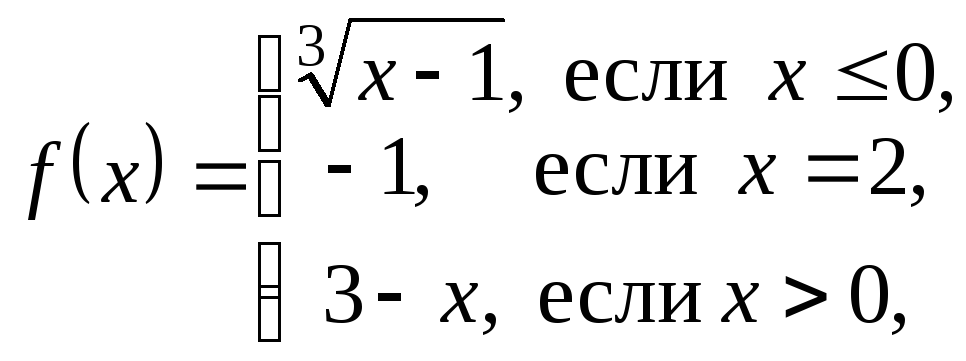 (см. рис. 2.6.6)
(см. рис. 2.6.6)
![]() – точка устранимого
разрыва, так как
– точка устранимого
разрыва, так как
![]() ,
,
![]() ,
т.е. односторонние пределы функции
,
т.е. односторонние пределы функции
![]() в точке
в точке
![]() существуют, конечны, равны между собой,
но не равны значению функции в этой
точке. Разрыв можно устранить, если
вместо
существуют, конечны, равны между собой,
но не равны значению функции в этой
точке. Разрыв можно устранить, если
вместо
![]() при
при
![]() придать функции значение
придать функции значение
![]() .
.
Определение.
![]() называется точкой
разрыва II
–го рода
функции
называется точкой
разрыва II
–го рода
функции
![]() ,
если хотя бы один из односторонних
пределов (слева или справа) функции в
этой точке не существует или равен
бесконечности.
,
если хотя бы один из односторонних
пределов (слева или справа) функции в
этой точке не существует или равен
бесконечности.
П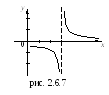 ример.
Функция
ример.
Функция
![]() – определена и непрерывна на всей
числовой оси кроме точки
– определена и непрерывна на всей
числовой оси кроме точки
![]() (см. рис. 2.6.7).
(см. рис. 2.6.7).
![]() – точка разрыва II-го
рода, так как
– точка разрыва II-го
рода, так как
![]() ;
;
![]() .
.
Аналогично, для
функции двух переменных
![]() ,
точки, в которых непрерывность нарушается,
называются точками
разрыва этой функции.
Эти точки могут образовывать целые
линии
разрыва.
,
точки, в которых непрерывность нарушается,
называются точками
разрыва этой функции.
Эти точки могут образовывать целые
линии
разрыва.
Пример.
Функция
![]() имеет линию разрыва
имеет линию разрыва
![]() .
.
