§3 Расчет режима линии при заданном токе нагрузки.

3.1 Задано напряжение в конце линии 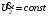. Известны ток нагрузки , напряжение , сопротивление и проводимость линии . Надо определить напряжение ток в продольной части линии , потери мощности в линии 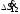и ток в начале линии

Расчет состоит в определении неизвестных токов и напряжений последовательно от конца линии к началу. Для определения токов и напряжений применяются первый закон Кирхгофа и закон Ома. Будем использовать фазные напряжения и токи. Емкостный ток в конце линии 12, соединяющей узлы 1 и 2, по закону Ома:.

Ток в продольной части линии по первому закону Кирхгофа: .

Напряжение в начале линии по закону Ома: .

Емкостный ток в начале линии: .

Ток в начале линии: .

Потери мощности в линии (в трех фазах) .

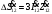Векторные диаграммы токов и напряжений:

а) В случае нагрузки в конце линии :

б) В режиме холостого хода :

3.2 Задано напряжение в начале линии . Известны . Надо определить . В данном случае невозможно, как ранее последовательно от конца линии к началу определить неизвестные токи и напряжения, используя первый закон Кирхгофа и закон Ома.

В этом случае используется уравнение узловых напряжений для узла 2: ,

где: - взаимная проводимость узлов 1 и 2, равная сумме проводимостей ветвей, соединяющих эти узлы и взятой с обратным знаком; — собственная проводимость узла 2, равная сумме проводимостей ветвей, соединенных с узлом 2:

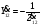
Тогда:

Ток в продольной части схемы замещения: .

Зарядный ток в начале линии:

Согласно закону Кирхгофа, ток в начале линии:

Потери мощности в линии вычисляются аналогично п.3.1.

§4 Расчет режима линии при заданной мощности нагрузки.

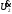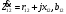4.1 Задано напряжение в конце линии . Известны мощность нагрузки , напряжение , сопротивление и проводимость линии . Надо определить напряжение мощности в конце и в начале продольной части линии , потери мощности , мощность в начале линии

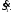
Расчет аналогичен расчету, приведенному в § 3.1, и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании первого закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения. Зарядная (емкостная) мощность трех фаз в конце линии:

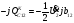
Мощность в конце продольной части линии по первому закону Кирхгофа:

Потери мощности в линии:

Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии:

Линейное напряжение в начале лини:

Емкостная мощность в начале линии

Мощность в начале линии:

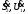
4.2 Задано напряжение в начале линии . Известны . Надо определить .

В данном случае невозможно последовательно от конца линии к началу определить неизвестные токи и напряжения по первому закону Кирхгофа и закону Ома, так как - неизвестно. Нелинейное уравнение узловых напряжений для узла 2 имеет следующий вид:

Это уравнение можно решить и найти неизвестное напряжение , а затем найти все мощности по выражениям п.4.1. Способы решения нелинейных уравнений узловых напряжений трудны и реализуются с помощью ЭВМ

Однако можно осуществить приближенный расчет в два этапа.

1-й этап. Предположим, что и определим потоки и потери мощности аналогично выражениям п.4.1, используя номинальное напряжение в конце лини: ; .

2-й этап. Определим напряжение по закону Ома, используя поток мощности , найденный в 1-м этапе. Для этого используем закон Ома, выразив ток через и :

Потоки мощности на 1-м этапе определены приближенно, поскольку при определении потоков мощности вместо использовали . Соответственно напряжение на 2-м этапе также определено приближенно. Возможно итерационное повторение расчета.