Универсальность математических моделей

Рассмотрим процессы колебаний в объектах различной природы. Покажем, что несмотря на разную сущность объектов, им соответствуют одни и те же математические модели.

1. Жидкость в u – образном сосуде.

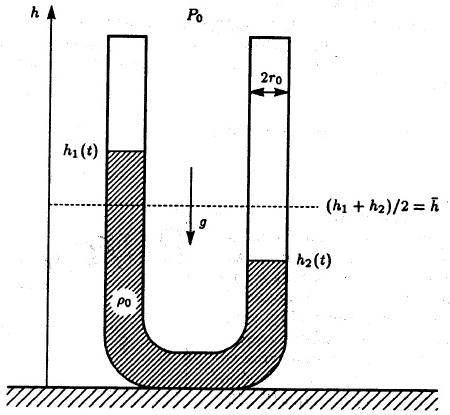
Жидкость занимает часть сосуда U – образной формы, представляющего собой изогнутую трубку радиуса . Масса жидкости , ее плотность . Стенки сосуда идеально гладкие, поверхностным натяжением пренебрегается, атмосферное давление 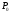и ускорение свободное падение постоянны.

В состоянии равновесия жидкость, очевидно, покоится, ее высота в обоих коленах сосуда одинакова. Если ее вывести из равновесия, то начнется движение, характер которого установим с помощью закона сохранения энергии, поскольку в силу сделанных предположений ее потери в системе отсутствуют.

Потенциальную энергии системы вычислим через работу, которую необходимо совершить, чтобы переместить ее из состояния равновесия (где ) в положение неравновесия.

Она равна

, , ,

где 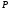- вес той части жидкости в левом колене, уровень которой превышает величину 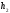. Работа сил атмосферного давления равна нулю, так как для разных колен соответствующие перемещения направлены в разные стороны.

Неизвестные величины 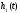и связаны очевидным соотношением , выражающим постоянство полной длины столба жидкости в сосуде с постоянным сечением. Поставляя последнее равенство в выражение для 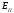, получаем после интегрирования

.

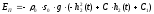При вычислении кинетической энергии учтем постоянство сечения трубки и несжимаемость жидкости. Это означает, что столб жидкости движется как целое, и ее скорость одинакова во всех сечениях. Примем за величину , и тогда

,

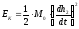а из закона сохранения энергии следует

.

Так как 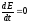, то продифференцировав это выражение, получаем

,

что с учетом такого же соотношения для величины 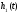, дает уравнение

,

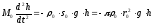где - отклонение уровня жидкости от положения равновесия. Оно с точностью до обозначений совпадает с уравнением для системы «шарик – пружина» (в данном случае аналогом шарика служит столб жидкости, а роль пружины играет тяготение). Последовательный отказ от идеализации объекта дает более полные его модели.

2. Колебательный электрический контур.

Это устройство представляет собой конденсатор, соединенный проводами с индуктивной катушкой. В момент цепь замыкается, и заряд с обкладок конденсатора начинает распространяется по цепи.

Сопротивление проводов будем считать равным нулю, емкость конденсатора равна , индуктивность катушки 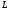. Для изменяющейся со временем величины 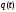, где 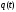- заряд на обкладках конденсатора, необходимо получить соответствующее уравнение. Очевидно, что ток и напряжение также являются функциями времени. По физическому смыслу величины 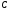в любой момент времени имеет место равенство (емкость равна величине заряда, который необходимо поместить на обкладки конденсатора для увеличения разности потенциалов между ними на единицу).

Так как электрическое сопротивление в цепи отсутствует, то падение напряжения на проводах нет, и разность потенциалов , существующая на конденсаторе, подается непосредственно на катушку. При переменном токе в катушке возникает электродвижущая сила самоиндукции, равная . Закон Ома в цепи в отсутствие сопротивления выглядит следующим образом

,

или

.

Так как по определению (при изменении заряда на конденсаторе в цепи возникает ток), то из последнего соотношения получаем выражение

,

описывающее процесс колебаний величины (а, следовательно, и величин и ) в простейшем электрическом контуре. В системе «емкость – индуктивность» колебания происходят также, как и в системе «шарик – пружина».