3. Геометрическая интерпретация задач линейного программирования

Рассмотрим такой пример:

максимизировать 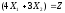, при условиях

, , , .

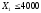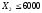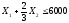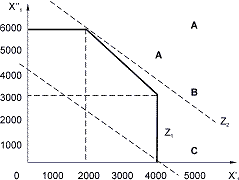
Рис. 4.1

Каждое из этих неравенств определяет полуплоскости, пересечение которых дает многоугольник, «заштрихованный» на рис. 4.1. Этот многоугольник (выпуклый многогранник) и представляет собой допустимое множество решений 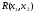задачи ЛП.

Теперь рассмотрим целевую функцию

,

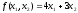пусть ее значения

.

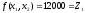График уравнения 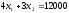- прямая с отрезками на осях , .

.

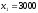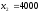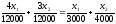При 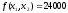получим прямую .

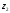Прямая 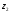параллельная прямой , но расположена выше от нее. Передвигая прямую вверх параллельно самой себе, приходим к такому ее положению, когда прямая и множество 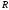будут иметь только одну общую точку .

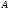Очевидно, что точка 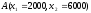- оптимальное решение, так как она лежит на прямой с максимально возможным значением 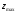. Заметим, что эта точка оказалась крайней точкой множества .

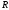При векторной форме ограничения задачи ЛП записываются так:

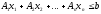, (3.1)

где

, , …, .

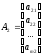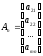Рассмотрим допустимое множество в пространстве данных векторов.

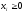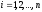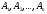Поскольку в формуле (3.1) , , то все положительные комбинации векторов образуют конус. Поэтому вопрос о существовании допустимых решений равнозначен вопросу о принадлежности вектора 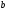этому конусу.

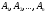
Поскольку 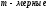векторы 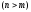, то среди них всегда обнаружится 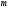линейно-независимых векторов, образующих базис 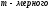пространства и содержащих конус, образованный векторами .

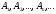Поэтому справедливо следующее утверждение. Если задача ЛП содержит переменных и 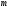ограничений, записанных в форме неравенств 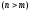, не считая ограничений неотрицательности переменных 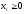, то в оптимальное решение входит не более чем 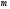ненулевых компонент вектора .

Расширенная форма задачи ЛП. Для решения задач ЛП необходимо переходить от ограничений - неравенств к ограничениям в форме уравнений. Для этого в каждое неравенство вводят по одной свободной переменной ,,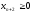…,,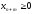 чтобы превратить его в равенство.

В таком виде задачу ЛП называют расширенной и записывают так:

максимизировать

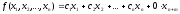, (3.2)

при ограничениях

,

,

…………………………………………………………………

.

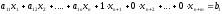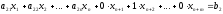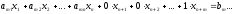В матричной форме эта задача имеет следующий вид:

максимизировать ,

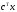при ограничениях

,

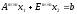где

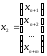, . (3.3)

Наконец, векторная форма записи расширенной задачи ЛП:

максимизировать ,

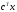при ограничениях

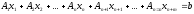. (3.4)

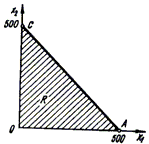
Рис. 3.1

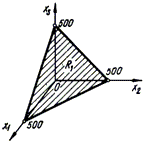
Рис. 3.2

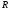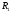Пусть и - допустимые множества решений исходной и расширенной задач соответственно. Тогда любой точке допустимого множества решений 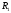соответствует единственная точка множества 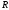, и наоборот.

Установим отношение между элементами 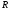и :

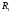исходная задача: ,

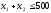расширенная задача: .

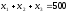На рис. 3.1 и 3.2 изображены допустимые множества решений обеих задач.

Очевидно, что треугольник ОСА (рис. 3.1) - допустимое множество 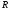- есть проекция допустимого множества 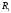(рис. 3.2) на подпространство .

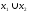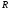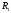В общем случае допустимое множество решений исходной задачи есть проекция допустимого множества решений расширенной задачи на подпространство исходных переменных .

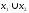Лекция №11.

Нелинейное программирование. Классификация методов нелинейного программирования. Задача нелинейного программирования при ограничениях неравенствах. Геометрическая интерпретация задач нелинейного программирования