
- •Лекции по математическому моделированию
- •Математическое моделирование. Математическая модель в задачах оптимизации. Элементарные математические модели
- •Элементарные математические модели
- •Примеры моделей, получаемых из фундаментальных законов природы
- •4. Движение шара, присоединенного к пружине
- •Вариационные принципы и математические модели
- •Общая схема принципа Гамильтона.
- •Третий способ получения модели системы «шарик – пружина».
- •3. Колебания маятника в поле сил тяжести
- •4. Заключение
- •Универсальность математических моделей
- •1. Жидкость в u – образном сосуде.
- •2. Колебательный электрический контур.
- •3. Малые колебания при взаимодействии двух биологических популяций.
- •4. Заключение.
- •Сохранение массы вещества
- •1. Поток частиц в трубе.
- •2. Основные предположения о гравитационном режиме течения грунтовых вод.
- •3. Баланс массы в элементе грунта.
- •4. Замыкание закона сохранения массы.
- •5. О некоторых свойствах уравнения Буссинеска.
- •6. Основные выводы.
- •Сохранение энергии
- •1. Предварительные сведения о процессах теплопередачи.
- •2. Вывод закона Фурье из молекулярно-кинетических представлений.
- •3. Уравнение баланса тепла.
- •4. Постановка типичных краевых условий для уравнения теплопроводности.
- •5. Об особенностях моделей теплопередачи.
- •Совместное применение нескольких фундаментальных законов
- •1. Предварительные понятия газовой динамики.
- •2. Уравнение неразрывности для сжимаемого газа.
- •3. Уравнения движения газа.
- •4. Уравнение энергии.
- •Фильтрация смеси нефти и воды в пористой среде
- •Математическая модель фильтрации
- •Модель переноса примеси при однокомпонентной фильтрации
- •Модель переноса примеси при многокомпонентной фильтрации
- •Математическое моделирование физических процессов
- •1. Изменение атмосферного давления с изменением расстояния от поверхности Земли.
- •2. Задача об остывании тела.
- •3. Падение тел у земной поверхности.
- •4. Режимы течения. Вязкость. Число Рейнольдса.
- •5. Формула Стокса.
- •6. Сила гидравлического сопротивления.
- •Математическое программирование. Понятие линейного программирования. Виды задач линейного программирования. Геометрическая интерпретация задач линейного программирования
- •1. Понятие математического программирования
- •2. Понятие линейного программирования. Виды задач линейного программирования
- •3. Геометрическая интерпретация задач линейного программирования
- •1. Понятие нелинейного программирования
- •2. Классификация методов нелинейного программирования
- •2.1. Задача нелинейного программирования при ограничениях – неравенствах
- •4. Геометрическая интерпретация задач нелинейного программирования
Вариационные принципы и математические модели
Дадим упрощенную формулировку вариационного принципа Гамильтона для механической системы. На его основе выведем уравнения движения на пружине и маятника в поле сил тяжести. Сопоставим результаты получения моделей из фундаментальных законов и вариационного принципа.
-
Общая схема принципа Гамильтона.
Пусть
имеется механическая система, формального
или строгого определения которой пока
давать не будем, имея в виду, что все
взаимодействия между элементами такой
системы определяются законами механики
(один из простейших примеров, система
«шарик – пружина»). Ведем понятие
обобщенных
координат
 ,
полностью определяющих положение
механической системы в пространстве.
Величина
,
полностью определяющих положение
механической системы в пространстве.
Величина
 может
быть декартовой координатой (например,
координата
может
быть декартовой координатой (например,
координата
 в
системе «шарик – пружина»), радиусом-вектором,
угловой координатой, набором координат
материальных точек, составляющих систему
и т.д. Величину
в
системе «шарик – пружина»), радиусом-вектором,
угловой координатой, набором координат
материальных точек, составляющих систему
и т.д. Величину
 естественно
называть обобщенной
скоростью
механической системы в момент времени
естественно
называть обобщенной
скоростью
механической системы в момент времени
 .
Набор величин
.
Набор величин
 и
и
 определяет
состояние механической системы во все
моменты времени.
определяет
состояние механической системы во все
моменты времени.
Для описания механической системы вводится функция Лагранжа, которая, в простейших случаях, имеет явный смысл и записывается в следующем виде
 , (1)
, (1)
где
 и
и
 -
кинетическая и потенциальная энергии
соответственно.
-
кинетическая и потенциальная энергии
соответственно.
Введем
величину
 ,
называемой действием:
,
называемой действием:
 . (2)
. (2)
Интеграл
(2), очевидно, является функционалом от
обобщенной координаты
 ,
т.е. функции
,
т.е. функции
 ,
заданной на отрезке
,
заданной на отрезке
 ,
он ставит в соответствие некоторое
число
,
он ставит в соответствие некоторое
число
 (действие).
(действие).
Принцип
Гамильтона для механической системы
гласит: если система движется по законам
механики, то
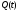 -
стационарная функция для
-
стационарная функция для ,
или
,
или
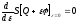 . (3)
. (3)
Фигурирующая
в принципе
наименьшего действия
(3) функция
 -
некоторая пробная функция, обращающаяся
в ноль, в моменты
-
некоторая пробная функция, обращающаяся
в ноль, в моменты
 и
удовлетворяющая тому условию, что
и
удовлетворяющая тому условию, что
 -
возможная координата данной системы
(в остальном
-
возможная координата данной системы
(в остальном
 произвольна).
произвольна).
Смысл
принципа (3) в том, что из всех априори
мыслимых (допускаемых) траекторий
(движений) системы между моментами
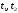 выбирается
(реализуется) движение, доставляющее
минимум функционалу действие (отсюда
и происходит название принципа). Функция
выбирается
(реализуется) движение, доставляющее
минимум функционалу действие (отсюда
и происходит название принципа). Функция
 называется
вариацией
величины
называется
вариацией
величины
 .
.
Итак,
схема применения принципы Гамильтона
(3) для построения моделей механических
систем состоит в следующем: определяются
обобщенные координаты
 и
обобщенные скорости
и
обобщенные скорости
 системы,
строятся функция Лагранжа
системы,
строятся функция Лагранжа
 и
функционал действия
и
функционал действия
 ,
минимизация которого на вариациях
,
минимизация которого на вариациях
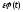 координаты
координаты
 и
дает искомую модель.
и
дает искомую модель.
-
Третий способ получения модели системы «шарик – пружина».
Воспользуемся
принципов Гамильтона для построения
модели движения шарика, соединенного
с пружиной. В качестве обобщенной
координаты системы естественно выбрать
обычную эйлерову координату шарика
 .
Тогда обобщенная скорость
.
Тогда обобщенная скорость
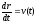 -
обычная скорость шарика. Функция Лагранжа
(1), равная
-
обычная скорость шарика. Функция Лагранжа
(1), равная
 ,
записывается через значения кинетической
и потенциальной энергии системы:
,
записывается через значения кинетической
и потенциальной энергии системы:
 .
.
Для величины действия получаем выражение
 .
.
Теперь
в соответствии со схемой, вычислим
действия на вариациях
 координаты
координаты :
:
 .
.
Последнюю
формулу необходимо продифференцировать
по
 (учитывая, что функции
(учитывая, что функции
 от
от
 не
зависят):
не
зависят):
 ,
,
и
положить в нее
 :
:
 .
.
Правая
часть этого выражения (равного нулю в
согласии с принципом Гамильтона) с
помощью интегрирования ее первого члена
по частям и с учетом того, что
 в
моменты
в
моменты
 ,
преобразуется к виду:
,
преобразуется к виду:
 .
.
Поскольку
пробная функция
 ,
фигурирующая в формулировке принципа
наименьшего действия, произвольна, то
часть выражения, стоящая под знаком
интеграла в квадратных скобках, должна
быть равна нулю во все моменты времени
,
фигурирующая в формулировке принципа
наименьшего действия, произвольна, то
часть выражения, стоящая под знаком
интеграла в квадратных скобках, должна
быть равна нулю во все моменты времени
 :
:
 ,
,
т.е. движение системы должно описываться уравнением, полученным из закона Ньютона (первый способ) и закона сохранения энергии (второй способ). Все три подхода эквивалентны.
