3. Модель переноса примеси при многокомпонентной фильтрации

Обобщим уравнение (9) на случай многокомпонентной фильтрации. Предполагается, что фазы (вода и нефть) не смешиваются, и пассивная примесь может иметь ненулевую концентрацию только в воде и на стенках пор. Концентрация воды во флюиде равна . Поле скоростей фильтрации воды равно . Тогда поле скоростей течения воды определено в тех точках, где вода присутствует, и равно

.

Рассмотрим произвольный объём пористой среды. Закон сохранения количества примеси для этого объёма имеет вид:

, (10)

где:

— концентрация примеси;

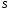— граница объёма ;

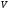— плотность потока примеси;

— нормаль к поверхности ;

— плотность мощности источников примеси.

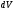Рассмотрим малый объём . Количество растворённой примеси в объёме равно . Часть объёма занята водой. Соответственно в этой части объёма имеем 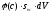молей примеси, адсорбированной на стенках пор. Так как примесь может иметь ненулевую концентрацию только в воде, то она не сможет из адсорбированного состояния перейти в нефть. Поэтому в части объёма, занятой нефтью, плотность адсорбированной примеси будет такая же, как и в части объёма, заполненной водой. В итоге во всём объёме имеем молей адсорбированной примеси.

Тогда суммарное количество примесей в объеме 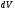равно

. (11)

Рассмотрим некоторую малую площадь в пористой среде. Так как примесь может передвигаться только в воде, то достаточно рассмотреть поток через занятую водой часть этой площади.

Конвективный поток будет равен

.

Диффузионный поток будет равен

.

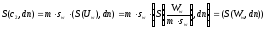Тогда суммарный поток примеси через площадь будет равен

. (12)

Закон сохранения массы (10) с учетом (11) и (12) запишется в виде

.

Отсюда

. (13)

Так как объём 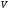не зависит от времени, можно поменять местами дифференцирование по времени и интегрирование в первом слагаемом. Тогда, в силу произвольности , будем иметь:

, (14)

где:

— пористость;

— концентрация примеси;

— водонасыщенность;

— концентрация адсорбированной в порах примеси;

— скорость фильтрации воды;

— диффузионный поток, вызванный конвективной диффузией;

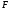— плотность мощности источников примесей.

Скорость фильтрации воды может быть определена в соответствии с обобщённым законом Дарси:

. (15)

Лекция №9.

Математическое моделирование физических процессов

1. Изменение атмосферного давления с изменением расстояния от поверхности Земли.

Примем следующие предположения для математической модели: 1) температура воздуха не зависит от высоты над поверхностью; 2) воздух является идеальным газом; 3) гравитационные силы подчиняются закону Ньютона.

Тогда можно показать, что давление 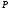на расстоянии от центра Земли удовлетворяет уравнению:

, (1)

причем на поверхности Земли , .

Здесь 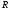– радиус Земли, (– гравитационная постоянная, – масса

Земли, – ускорение свободного падения, – константа). Если эти параметры выбраны в одной и той же системе единиц, отношение .

Уравнение (1) удобно привести к безразмерному виду. Для этого введем новые переменные: , , . Так как , то пренебрегая величиной , уравнение (1) сведем к виду:

. (2)

Начальное условие, которое обеспечивает единственность решения, формулируется как .