
- •Глава 2. Кинематика твёрдого тела
- •§ 11. Поступательное и вращательное движения твёрдого тела
- •3. Дополните предложения, вставляя пропущенные слова.
- •§12. Сложение поступательного и вращательного движений. Плоское движение. Мгновенная ось вращения
- •1. Дополните предложения, вставляя пропущенные слова.
- •§13. Примеры решения задач о плоском движении твёрдых тел
§13. Примеры решения задач о плоском движении твёрдых тел
1. Стержень длиной l = 0,85 м скользит по плоскости. В некоторый момент времени модули скоростей концов стержня стали равными v1 = 1 м/с и v2 = 1,5 м/с. При этом скорость первого конца стержня направлена под углом = 30 к его оси. Определите угловую скорость вращения стержня вокруг его центра в этот момент времени.
2. Тонкая палочка АВ длиной L скользит по плоскости. В некоторый момент времени скорость конца А палочки оказалась направленной под углом к оси палочки, а её модуль равен v. При этом скорость второго конца палочки направлена под углом к оси палочки.
1) Определите точку С палочки, скорость которой направлена в этот момент времени вдоль её оси, и найдите модуль скорости этой точки. 2) Докажите, что модуль скорости точки С меньше модуля скорости любой другой точки палочки.
3. Тонкий прямой стержень АВ скользит по горизонтальной плоскости. В некоторый момент времени скорость центра стержня образует с его осью угол = 60° При этом модуль скорости конца А стержня равен v1 = 1 м/с, а скорость конца В перпендикулярна скорости конца А. Определите модуль скорости центра стержня в этот момент времени.
4.
Лодку подтягивают
к пристани высотой Н
с помощью верёвки, которую наматывают
на вал лебёдки (рис. 25). Радиус вала
лебёдки равен r.
Вал вращают с постоянной угловой
скоростью
![]() .
Определите скорость лодки в тот момент
времени, когда длина верёвки равна L.
.
Определите скорость лодки в тот момент
времени, когда длина верёвки равна L.

Рис. 25
5.
Колесо радиусом R
катится без проскальзывания по
горизонтальной прямолинейной дороге.
При этом центр колеса движется прямолинейно
с ускорением
![]() .
Определите модуль ускорения верхней
точки колеса в тот момент времени, когда
скорость его центра станет равной
.
Определите модуль ускорения верхней
точки колеса в тот момент времени, когда
скорость его центра станет равной
![]() .
.
6. Диск, поперечное сечение которого показано на рис. 26, движется по плоскости так, что в некоторый момент скорости его точек А и В параллельны плоскости и перпендикулярны оси диска, а их модули равны vA и vB. Определите модуль скорости точки С в этот момент времени, если АОС = и все указанные точки находятся на одинаковом расстоянии от оси диска.
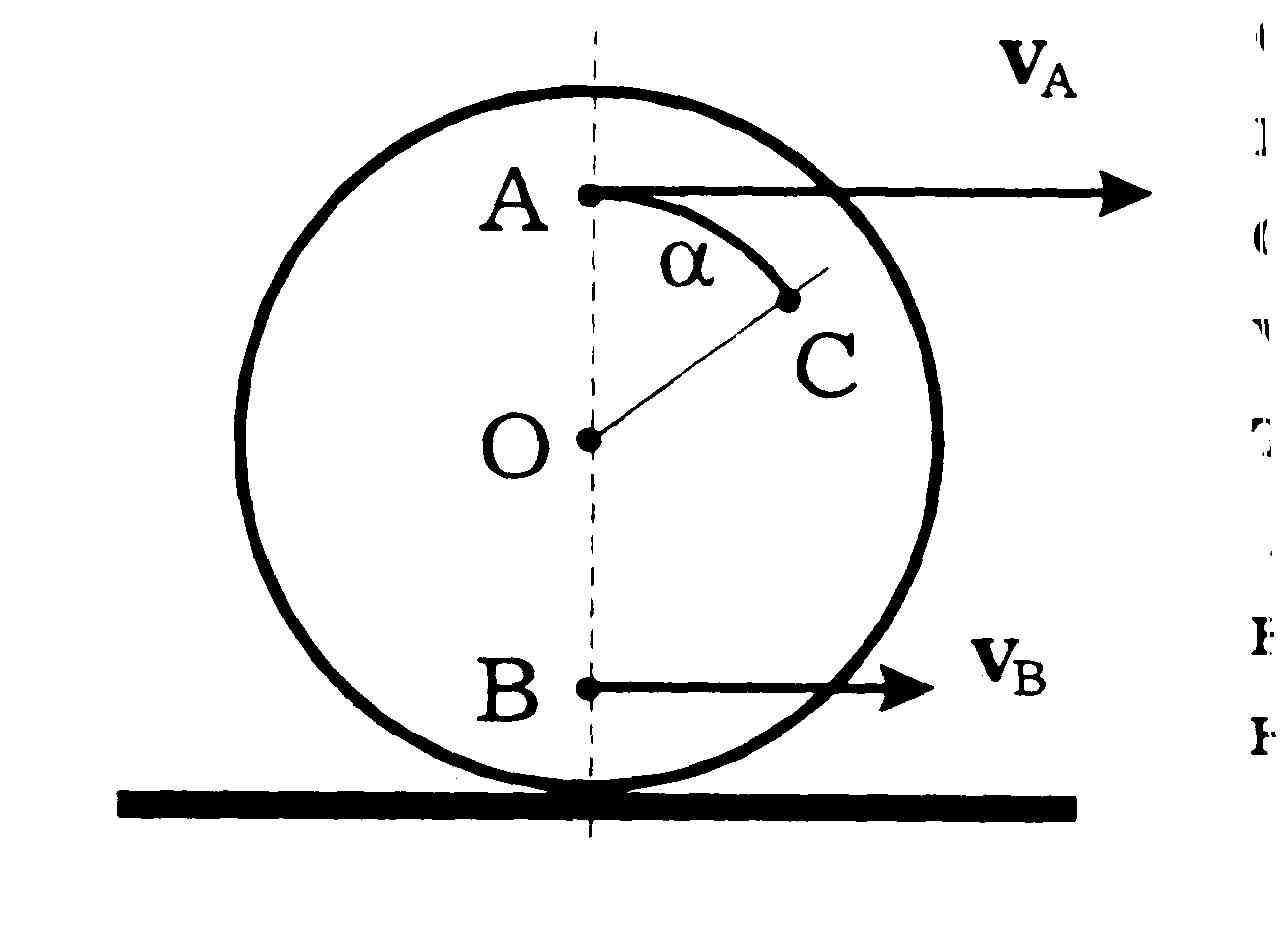
Рис. 26
7.
На цилиндрическую ось катушки радиусом
r
намотана лёгкая нерастяжимая нить,
отрезок АВ
которой горизонтален (рис. 27). Катушка
лежит на столе. В момент времени
![]() конец нити (точку А)
начинают тянуть с постоянным горизонтальным
ускорением а.
При этом катушка начинает двигаться
без проскальзывания так, что её ось не
изменяет своей ориентации. Через какое
время длина горизонтального участка
нити изменится в n
раз, если длина отрезка АВ
была равна L0,
а внешний радиус катушки равен R?
конец нити (точку А)
начинают тянуть с постоянным горизонтальным
ускорением а.
При этом катушка начинает двигаться
без проскальзывания так, что её ось не
изменяет своей ориентации. Через какое
время длина горизонтального участка
нити изменится в n
раз, если длина отрезка АВ
была равна L0,
а внешний радиус катушки равен R?
8*. По горизонтальной крышке стола катятся два цилиндра, на которых лежит доска (рис. 28). Оси цилиндров параллельны, и они движутся без проскальзывания относительно стола и доски. Определите модуль скорости доски относительно стола в тот момент, когда модуль относительной скорости ближайших друг к другу точек цилиндров станет равным v, а плоскость доски образует с плоскостью крышки стола угол .
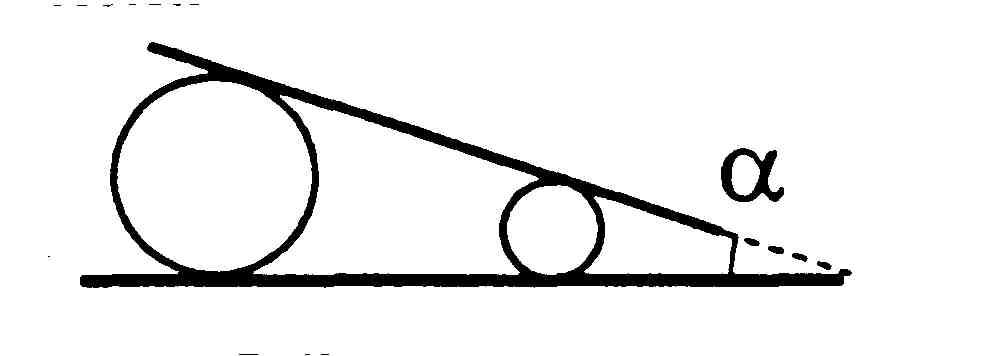
Рис. 28
9.
Равносторонний треугольник АВС
скользит по горизонтальному столу (рис.
29). Известно, что в некоторый момент
времени модуль скорости точки А
равен vА,
а модуль скорости
точки В
– vВ.
При этом скорость
![]() центра треугольника направлена
параллельно стороне СВ.
Определите модуль скорости центра
треугольника в этот момент времени.
центра треугольника направлена
параллельно стороне СВ.
Определите модуль скорости центра
треугольника в этот момент времени.
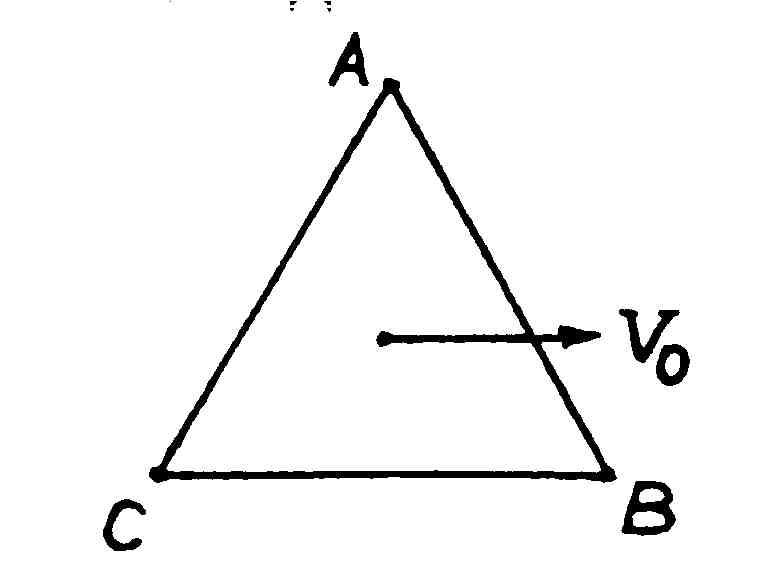
Рис. 29
10.
В некоторый момент времени скорости
вершин А
и В
скользящего по плоскости квадрата ABCD
оказались перпендикулярными друг другу,
а скорость вершины C
составила с прямой CD
угол, тангенс которого равен 0,5, и стала
равной
![]() .
Определите модуль скорости точки М,
являющейся серединой отрезка АВ.
.
Определите модуль скорости точки М,
являющейся серединой отрезка АВ.
11*. Катушку
(рис. 30) тянут за намотанную
на её среднюю часть лёгкую нерастяжимую
нить так, что её конец (точка А)
движется со скоростью
![]() под углом
под углом
![]() к горизонту. При этом катушка катится
без проскальзывания по горизонтальной
плоскости, а её ось не изменяет своего
направления. Определите модуль скорости
оси катушки, если радиус r
средней части катушки в
к горизонту. При этом катушка катится
без проскальзывания по горизонтальной
плоскости, а её ось не изменяет своего
направления. Определите модуль скорости
оси катушки, если радиус r
средней части катушки в
![]() раза меньше радиуса R
её щёк.
раза меньше радиуса R
её щёк.
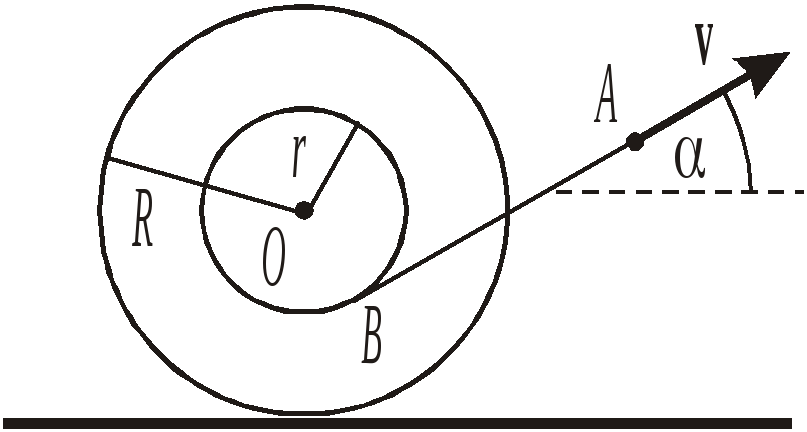
Рис. 30
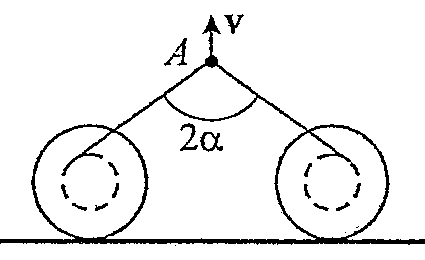
Рис. 31
