§12. Сложение поступательного и вращательного движений. Плоское движение. Мгновенная ось вращения

1. Дополните предложения, вставляя пропущенные слова.

Движение твёрдого тела называют плоским, если ___________________________________ _____________________________________

________________________________________________________________________

Любое плоское движение твёрдого тела в каждый момент времени можно рассматривать как суперпозицию ______________________________________________

Угловая скорость вращения твёрдого тела ____________________ от разбиения его плоского движения на поступательное и вращательное.

Скорость поступательного движения твёрдого тела ____________________от разбиения его плоского движения на поступательное и вращательное.

Плоское движение твёрдого тела в каждый момент времени можно представить как _________________________________________, которое совершается вокруг ___________________________оси.

2. Два автомобиля движутся по прямолинейной дороге. При этом модуль скорости центра колеса у первого автомобиля меньше, а у второго автомобиля — больше модуля скорости верхней точки этого же колеса, обусловленной его вращением. Какой из автомобилей будет замедляться, а какой — ускоряться? Ответ поясните.

3. Есть ли проскальзывание между колёсами автомобиля и дорожным покрытием, если скорость автомобиля 72 км/ч, а колёса вращаются с частотой 10 об/с? Радиус колеса равен 30 см. Каким при этом будет движение автомобиля?

4. Цилиндрическая бочка катится по Земле без проскальзывания. Скорость её центра равна по модулю v₀ = 2 м/с. Радиус бочки R = 0,5 м. Определите модули скоростей её точек А, В, С, D и Е ( рис. 19). Изобразите эти скорости (направление и модуль) на рисунке.

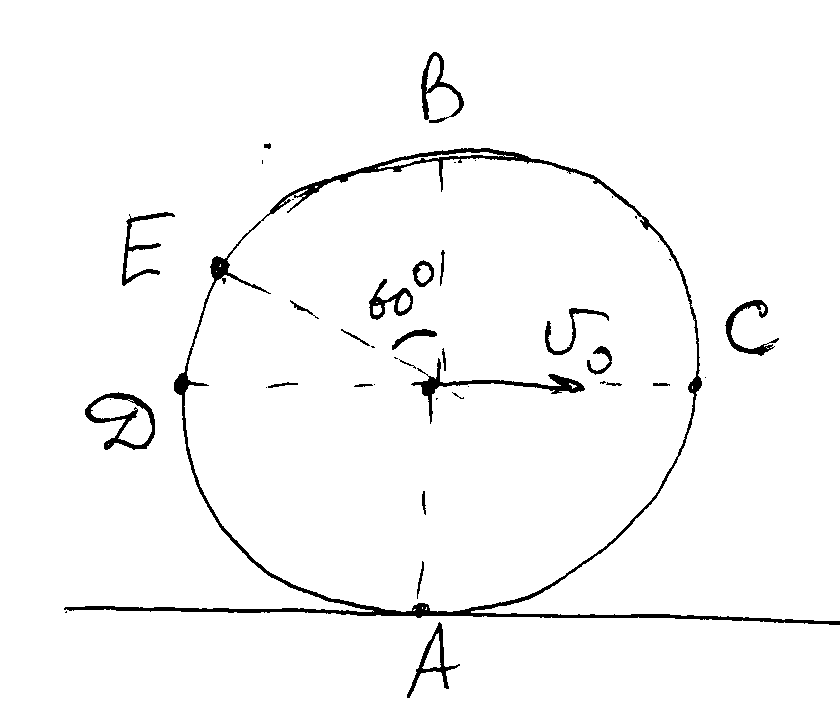
Рис. 19

5. Колесо катится без проскальзывания по Земле, вращаясь с угловой скоростью  = 4 рад/с. Радиус колеса R = 20 см. Определите модули скоростей точек А, В, С и D ( рис. 20). Изобразите эти скорости на рисунке.

Рис. 20

6. Диск катится без проскальзывания по горизонтальной поверхности. Скорости точек А и В, находящихся на одинаковом расстоянии от центра диска на его вертикальном диаметре, равны, соответственно, 10 м/с и 8 м/с (рис. 21). Радиус диска равен 10 см. Определите угловую скорость вращения диска и скорость движения его центра.

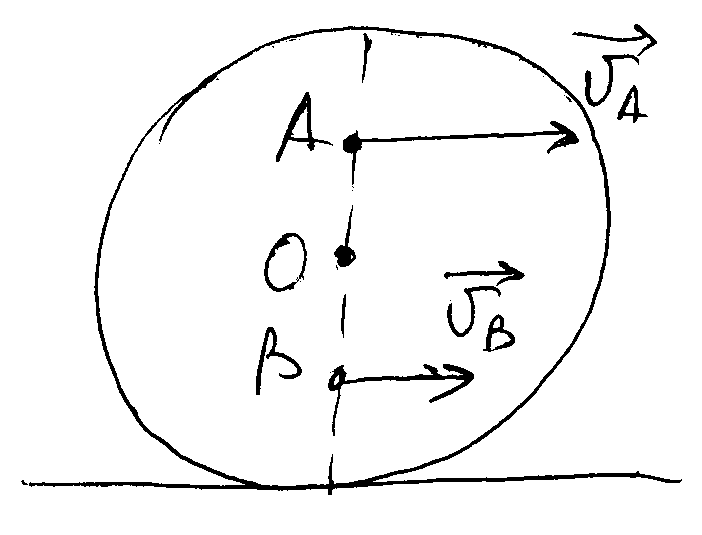
Рис. 21

7. Автомобиль едет по горизонтальной дороге без проскальзывания со скоростью, модуль которой равен v. В некоторый момент отрывается маленький камушек, застрявший в покрышке. На какую максимальную высоту над дорогой может подняться камушек, если точка отрыва расположена на высоте h < R от Земли, где R — радиус колеса.

8. Стержень, поперечное сечение которого показано на рис. 22, катится по горизонтальной плоскости без проскальзывания. Определите отношение модулей скоростей точек А и В, если ОА = ОВ и в n раз меньше радиуса стержня.

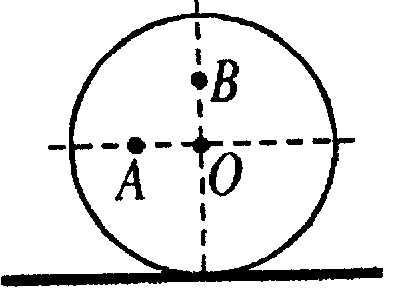
Рис. 22

9*. По ленте транспортёра (рис. 23), движущейся горизонтально со скоростью, модуль которой v_ = 1 м/c, в направлении её движения катится без проскальзывания колесо. Определите модуль u скорости центра колеса относительно Земли, если скорость точки В, находящейся на ободе колеса на его горизонтальном диаметре, относительно поверхности Земли образует с горизонтом угол  = 30.

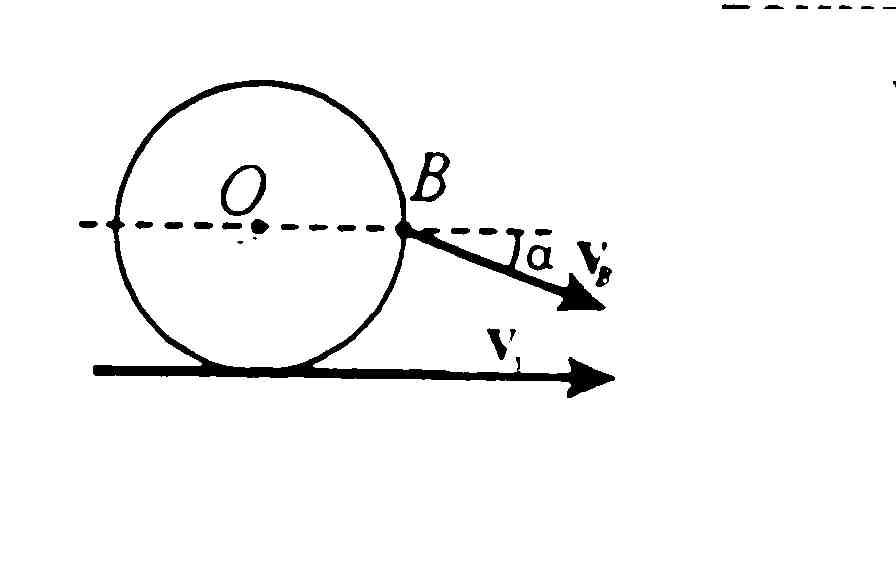
Рис. 23

10*. Цилиндрический каток радиуса R помещён между двумя параллельными рейками, которые движутся в одну сторону со скоростями, модули которых равны v₁ и v₂. Определите угловую скорость катка и скорость движения его центра при отсутствии проскальзывания.

11*. Кривошип ОА (рис. 24) вращается с угловой скоростью 2,5 с^-1, приводя в движение колесо радиуса r = 5 см, которое катится по неподвижному колесу радиуса R = 15 см. Определить скорость точки В.

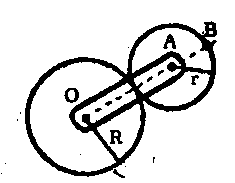
Рис. 24