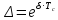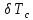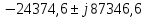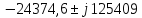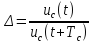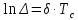Лабораторная работа №2 / Отчет

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Кафедра теории электрических цепей

ОТЧЁТ

по лабораторной работе №2 на тему: «Анализ переходных процессов в последовательном колебательном контуре с использованием программы FASTMEAN»

по дисциплине «Теория электрических цепей»

Выполнили: студенты группы ИКВТ-61, Козырев А.Б., Васюткин А.В., Гарифулина Т.С., Власов Д.В.

« » 2017 г. ___________/А.Б. Козырев/

Принял: к.т.н., доцент Замулин О. Л.

« » 2017 г. ___________/О.Л. Замулин/

1. Цель работы

С помощью программы FASTMEAN смоделировать переходные процессы в последовательном колебательном контуре и исследовать влияние параметров контура на режим колебаний.

2. Предварительные выкладки

При воздействии ступенчатого воздействия в контуре произойдёт накопление энергии на реактивных элементах во время действия импульса, после его окончания напряжение на конденсаторе и ток в цепи будут переходить в режим покоя. В зависимости от сопротивления цепи, этот переход может носить как колебательный или лимитационный характер.

Параметры цепи таковы:

Рассчитаем значение Скр, при котором возникает критический режим из соотношения

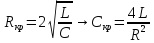
Заметим, что при таком значении сопротивления, корни характеристического уравнения, описывающего контур, будут кратными.

Где Q – добротность контура.

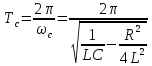
Где

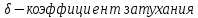
Где

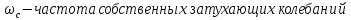
Где

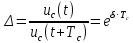
Где

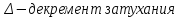
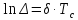
Рассчитаем и запишем корни характеристического уравнения, от дифференциального уравнения, описывающего последовательный колебательный контур.

Все расчеты удобно выполнять в среде Microsoft Office Excel.

Результаты предварительных расчетов приведены в таблицах 3.2, 3.3.

Покажем на комплексной плоскости расположение корней характеристического уравнения при всех указанных значениях ёмкости.

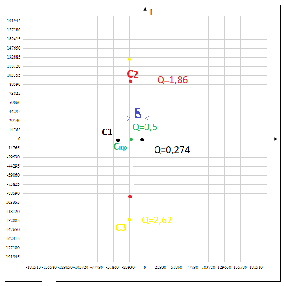
Таблица 3.2

Предварительный расчет	С, мкФ	Q	Тс, мкс
	С2	1,86	71,93	5,774	1,753
	С3	2,62	50,1	3,391	1,221
Результаты анализа на ПК			Измеряется по графикам			Вычисляется по данным измерений
			Тс				1/c
	С2		71,93	1,32	0,28
	С3

Таблица 3.3

С, мкФ	Q
	0,274	-3979,88931	-44769,3089
	0,5	-24374,5991	-24374,5991

3.2.

Схема собрана, заданы параметры RLC цепи. Генератор прямоугольных импульсов смоделирован.

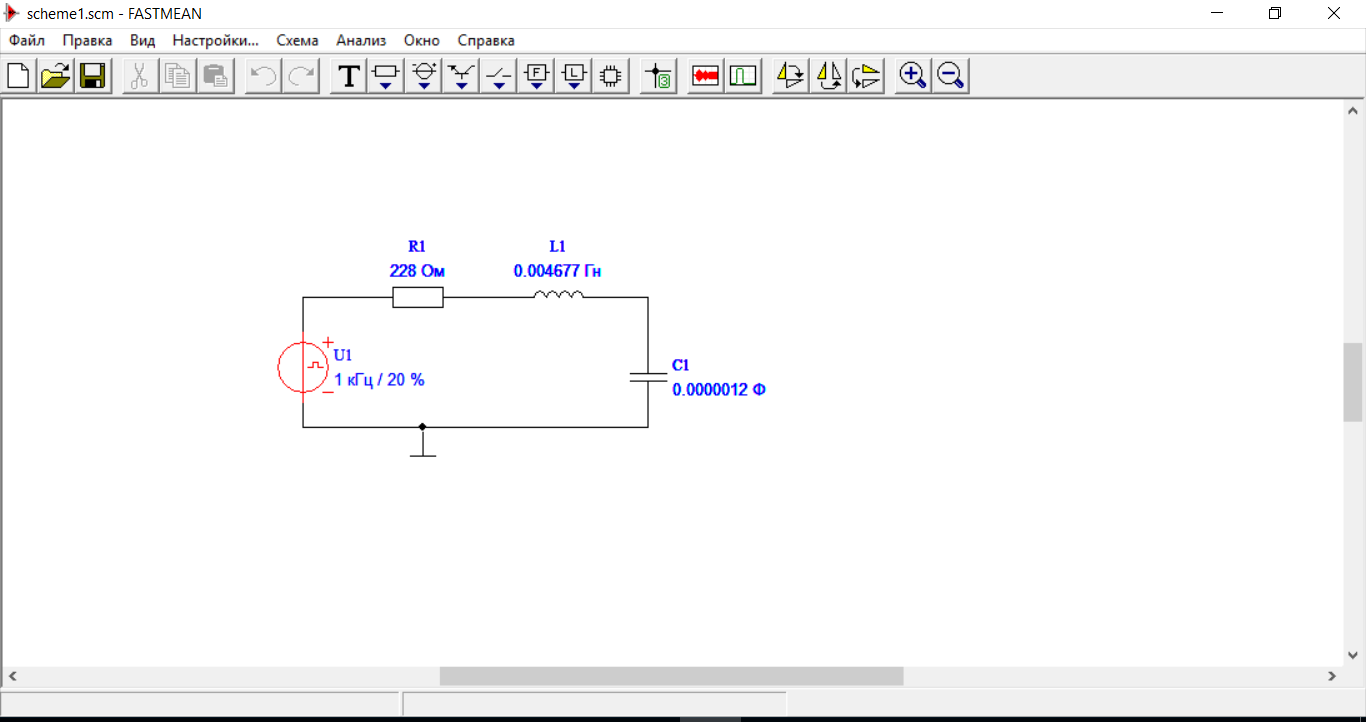
3.3.

Расчёт временных характеристик контура u_c(t), u_L(t) и u_R(t) с помощью анализа переходного процесса. Конечное время процесса выбрано 0,4 мс.

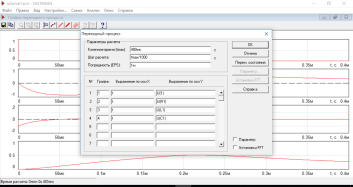
Построены графики напряжений на элементах.

Напряжение на ёмкости является непрерывной функцией времени, а на индуктивности терпит разрыв в момент окончания импульса.

Изобразим кривые на одном графике с учетом согласного выбора напряжений и токов.

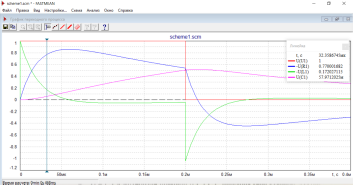
Имеется динамическая система II-порядка. Мы наблюдаем апериодический режим.

3.4.

Повторим моделирование переходного процесса для значения ёмкости .

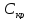При переходе в критический режим период свободных колебаний становится бесконечно большим, как видно на рисунке ниже.

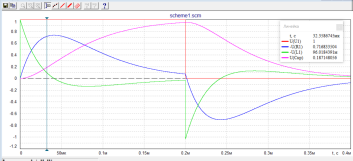
Этот режим характеризуется кратными корнями характеристического уравнения. Частота собственных затухающих колебаний стремится к нулю.

3.5.

Повторим моделирование переходного процесса для ёмкости C2. Большие ёмкости обладают инерционным свойством, ибо нужно сообщить больший заряд, чтобы увеличить напряжение на 1 В.

Возьмём маленькую ёмкость. Пусть это будет 0,026 мкФ.

Получаем затухающие свободные колебания, которые возникают после прекращения импульса.

3.5.

Определим период свободных колебаний T_c, с помощью линейки.

При этом учитываем, что легче рассчитать значение в области, которую легче локализовать.

При вычислении t1 = 10,0043254 мкс, t2 = 81,9382683 мкс.

Таким образом период свободных колебаний

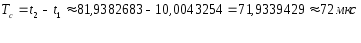
Через период известны уровни напряжений. За один период напряжение на индуктивности и резисторе падает в 5,7 раз.

Uc(t) = 1,416 В

Uc(t+Tc) = 1,072 В

Декремент затухания будет равен 1,32.

САНКТ-ПЕТЕРБУРГ 2017