1.5.2.Важнейшие дополнительные соотношения между термодинамическими величинами.

А. Уравнения Гиббса-Гелмгольца.

Эти уравнения позволяют переходить от одного термодинамического потенциала к другому, т.е. рассчитывать (в обобщенном выражении) Ψ_k(P_k), если дано Ψ_l(P_k): . На практике важнейшее значение имеют три частных случая уравнений Гиббса-Гелмгольца:

а) - позволяет рассчитывать энтальпию, если известна внутренняя энергия как функция давления.

б) - позволяет рассчитывать свободную энергию Гельмгольца, если известна внутренняя энергия как функция температуры.

в) - позволяет рассчитывать свободную энергию Гиббса, если известна энтальпия как функция температуры.

г) - позволяет рассчитывать свободную энергию Гиббса, если известна свободная энергия Гельмгольца как функция объема, например, из статистических расчетов.

д)- позволяет рассчитывать свободную энергию Гиббса, если известна энтальпия как функция температуры. Общее решение этого уравнения имеет вид: , где I – термодинамически неопределенная постоянная, зависящая от давления. В соответствие с теоремой Нернста (третьим законом термодинамики) при Т=0 I=0 и .

Уравнение д) является практически наиболее важным, так как применимо для наиболее часто встречающихся условий при анализе конденсированных материальных систем. Функцию Н(Т) можно получить интегрированием уравнения , если известна легко экспериментально определяемая величина теплоемкости при постоянном давлении. Величину G как функцию Т можно определить интегрированием уравнений в) и д): и соответственно, с определением констант интегрирования, или по уравнению г) без интегрирования, если F известна иp статистических расчетов. Уравнения д) можно также легко преобразовать в соотношение, которое можно записать в изменениях свободной энергии Гиббса и энтальпии , позволяющее определять тепловые эффекты () равновесных процессов (химических реакций, процессов растворения и фазовых переходов) через их «стандартную энергию Гиббса».

Б. Соотношения Максвелла.

Как уже указывалось, основные термодинамические функции состояния (U,S,F,G) являются характеристическими функциями многих независимых переменных, содержащих все термодинамические сведения о системе. Полный дифференциал функции многих переменных Y(x₁,x₂,…,x_n) выражается через первые частные производные в виде: , причем отдельные их слагаемые не являются дифференциалами, так как их интегралы мрогут принимать любые значения с учетом констант интегрирования. Первые частные производные таких функций по интенсивным независимым переменным дают экстенсивные параметры, а по экстенсивным – измеряемые и регулируемые интенсивные параметры , где Y – характеристическая функция, P_i - интенсивные и X_i - экстенсивные параметры (более подробно – см. раздел 3). Их вторые частные производные дают дополнительные измеримые величины. Воспользовавшись хорошо разработанной теорией таких функций и используя ее основополагающие соотношения (для трех переменных x,y,z, которые могут быть представлены к в виде функции двух других, т.е. 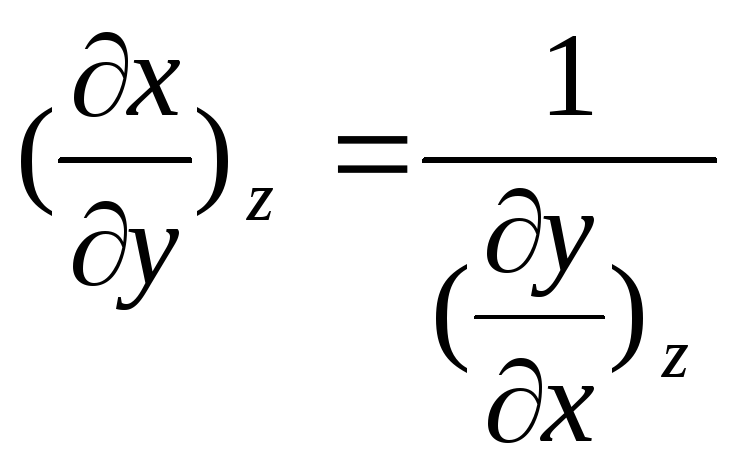x=х(y,z); y=у(х,z); z=z(х,у): (смешанные производные не зависят от порядка дифференцирования); и , а для двух разных функций одних и тех же переменных z=z(х,у) и f=f(x,y): ), Максвелл получил большое количество дополнительных соотношений между термодинамическими величинами, позволяющие связывать трудно измеряемые параметры с легко измеряемыми. Частными случаями соотношений Максвелла для внутренней энергии являются, например: ; , откуда т.е трудно определяемая величина, означающая прирост температуры на единицу объема при квазистаитчески-адиабатическом расширении, равна легко определяемому повышению давления при подводе единицы количества теплоты при постоянном объеме и составе.

Для термодинамических потенциалов в обобщенном выражении следует:,, (i,m≤k; j,n>k). Полученные при этом частные случаи соотношений Максвелла из свободных энергий Гельмгольца и Гиббса, а также из внутренней энергии и энтальпии чаще всего используются для представления производных термодинамических функций, которая легко может быть связана с экспериментально измеряемыми величинами. Например, вторая частная производная свободной энергии Гельмгольца как функции V и Т дает соотношение Максвелла в виде: а вторая частная производная свободной энергии Гиббса как функции р и Т - в виде: . В обоих соотношениях производную в правой части сравнительно легко определить экспериментально. Соотношения Максвелла позволяют выразить термодинамические производные через экспериментально определяемые величины, в частности (для однокомпонентных систем): мольную теплоемкость при постоянном давлении , где S_m - мольная энтропия; термический коэффициент объемного расширения и коэффициент изотермической сжимаемости (величину, обратную модулю объемного сжатия) , коэффициент давления разность мольных теплоемкостей при постоянном давлении и объеме, где V_m - мольный объем.

В.Уравнение Гельмгольца

Из условия независимости вторых производных фундаментального уравнения в энтропийном выражении по объему V и температуре Т (для закрытых систем) получено соотношение, получившее название уравнения Гельмгольца: , с помощью которого можно рассчитывать изотермические изменения внутренней энергии по известному уравнению состояния. С помощью этого уравнения можно показать, что для идеального газа с уравнением состояния pV=nRT внутренняя энергия при постоянной температуре не зависит от объема. Для N молей реального газа, состояние которого описывается уравнением Ван дер Ваальса : ; ; ; .