1.5.1. Основные типы термодинамических потенциалов

С учетом того, что внутренняя энергия и энтропия, наряду с общими свойствами экстенсивных параметров, обладают еще и особыми индивидуальными свойствами, вытекающими из законов термодинамики, вышеприведенное обобщенное определение термодинамических потенциалов позволяет в явном виде определить два наиболее важные с практической точки зрения термодинамических потенциала – свободные энергии Гельмгольца и Гиббса, являющиеся характеристическими функциями состояния.

А. Свободная энергия Гельмгольца

Свободная энергия Гельмгольца F(Т,V,N_k), как результат преобразования Лежандра функции U(S,V,N_k), в которой S заменена соответствующей частной производной, является характеристической функцией одного интенсивного (Т) и двух экстенсивных (V,N_k) параметров, и в соответствии с обобщенным определением термодинамического потенциала в интегральной () и дифференциальной () форме для многокомпонентной системы определяется следующим образом: F(T,V,N)=U-TS=-TS-PV+ и . Первые частные производные F по интенсивным параметрам дают экстенсивные параметры: , а по экстенсивным – интенсивные: (термическое уравнение состояния), . В закрытых системах уменьшение свободной энергии Гельмгольца равно работе, совершенной системой в изотермическом обратимом процессе. Как термодинамический потенциал свободная энергия Гельмгольца очень полезна при контролируемом объеме, т.е. в газообразных системах, а также при расчетах методами статистической термодинамики: F=-k_BlnZ, где k_B – константа Больцмана, Z - статистическая сумма (интеграл) по состояниям.

Б. Свободная энергия Гиббса и химический потенциал.

Свободная энергия Гиббса G(T,р,N_k), как результат преобразования Лежандра функции U(S,V,N_k), в которой S и V заменены соответствующими частными производными и , является характеристической функцией двух интенсивных (Т и р) и одного экстенсивного (N_k) параметров и в соответствии с обобщенным определением термодинамического потенциала в интегральной () и дифференциальной () форме определяется для многокомпонентных систем следующим образом: G(T,p,N)=U+pV-TS= -TS+pV+ и . Для закрытых систем уменьшение свободной энергии Гиббса равно работе, совершенной системой в изобарно-изотермическом обратимом процессе. Ее частные производные: ,(термическое уравнение состояния) и - химический потенциал, равный для однокомпонентных систем мольной свободной энергии Гиббса. Свободная энергия Гиббса и химический потенциал из всех термодинамических потенциалов находят наиболее широкое практическое применение при описании конденсированных систем, так как все независимые переменные в них (интенсивные р и Т, а также экстенсивный параметр - число молей компонентов N_i) легко измеряются и контролируются. Функция G(Т,р,N_k) часто используется в классической химической термодинамике в виде средней мольной величины:, которая в дифференциальной форме записывается как функция мольных долей компонентов х_i: . Последнее уравнение формально аналогично уравнению для dG, выведенное из обобщенного определения G: . Следовательно, средняя мольная величина G* является характеристической функцией, т.е. она содержит все термодинамические сведения о данной системе. Так, ее частные производные по интенсивным параметрам (р,Т) дают среднюю мольную энтропию и средний мольный объем: ,. Однако, частная производная средней мольной величины G* по мольной доле компонентов не является химическим потенциалом, в отличие от частного производного свободной энергии Гиббса G(Т,р,N_k) по числу молей компонентов: , которое является химическим потенциалом компонентов . При этом , а .

Химический потенциал как парциальная мольная (для многокомпонентных систем) или просто мольная g (для однокомпонентных систем) свободная энергия Гиббса связан с температурой и парциальными мольными величинами функций состояния S и H: и аналогичными соотношениями: ; .

Уравнение Гиббса-Дюгема с использованием частных производных как свободной энергии Гиббса G, так и ее средней мольной величины G* по интенсивным переменным, а также частных производных химического потенциала по числу молей и мольным долям формально имеет аналогичный вид для общих и изобарно-изотермических условий или процессов соответственно:

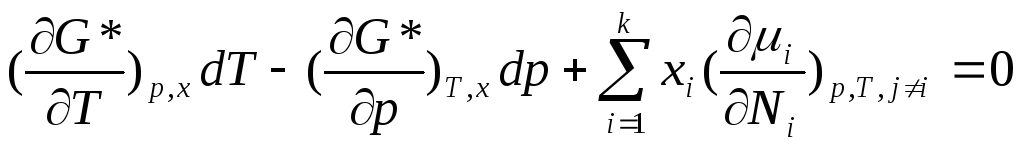и; ; и .

В.Энтальпия

Преобразованием Лежандра функции U(S,V,N_k), в которой V заменена соответствующей частной производной , качестве термодинамического потенциала может быть введена также энтальпия Н(S,р,N_k). Она является функцией одного интенсивного (р) и двух экстенсивных (S,N_k) параметров. В интегральной и дифференциальной форме уравнения для энтальпии записываются следующим образом: Н=U+pV и , а ее частные производные дают: ; ;. Однако, применение энтальпии как термодинамического потенциала не удобно, так как функция Н(S,р,N_k) содержит энтропию в качестве независимой переменной, которую невозможно контролировать. Поэтому в классической термодинамике энтальпию, по аналогии с внутренней энергией, обычно представляют (в общем случае для многокомпонентной системы) как функцию двух интенсивных (T,р) и одной экстенсивной (N) переменных, которая не является характеристической функцией, так как изменение этой функции (ее полный дифференциал) представляет собой дифференциальное уравнение первого порядка в частных производных: , решение которого содержит произвольную функцию. Следовательно, энтальпия не является в этом случае термодинамическим потенциалом, и, соответственно, частная производная не является химическим потенциалом. При этом частная производная соответствует практически очень важному параметру - мольной теплоемкости при постоянном давлении, поэтому энтальпия как функция Н(T,р,N) широко используется для анализа тепловых эффектов в различных процессах. Энтальпия впервые была введена и наиболее широко применяется при анализе теплоты , выделяемой или поглощаемой в равновесных обратимых процессах (химических реакциях и фазовых переходах) в закрытых системах при постоянном давлении и составе. Было установлено, что эта теплота обусловлена изменением внутренней энергии и работой, совершаемой за счет изменения объема системы при ее переходе из начального в конечное состояние: . Величина представляет собой разницу величин: , не зависящих от пути, по которому они были достигнуты в закрытой систем. Следовательно, Н= является функцией состояния, определяемой независимыми переменными р и Т, и равна внутренней энергии за вычетом работы, произведенной системой против внешнего давления при увеличении ее объема: . Так как в конденсированном состоянии изменение объема при любых превращениях в изобарных условиях при обычном (нормальном) давлении очень малы, и работа, совершаемая при этом также мала, изменение энтальпии в таких условиях практически равно изменению внутренней энергии.

Величина ,т.е. изменение энтальпии в закрытой системе при постоянном давлении равно тепловому эффекту соответствующего равновесного обратимого процесса (смешения, химических реакций, фазового перехода) и характеризует тепловой эффект или энтальпию процесса, причем для экзотермических процессов, сопровождающихся выделением тепла (положительный тепловой эффект), энтальпия отрицательная, а для эндотермических, протекающих с поглощением тепла (отрицательный тепловой эффект), энтальпия положительная. Изменение энтальпии, как и внутренней энергии, в равновесных обратимых процессах обычно определяют относительно некоторого стандартного состояния.