22

Раздел 1. Исходные положения классической равновесной (технической и химической) термодинамики (РТД): основные определения, термодинамические функции состояния и независимые переменные, основные соотношения между ними.

1.1. Основные определения и термины

Термодинамика является разделом фундаментальной науки, посвященным обобщенному описанию тепловой и других форм энергии, её передачи  и изменения (преобразования из одной формы в другую) в различных системах и процессах. Термодинамика основана на наиболее общих принципах, которые являются универсальными и базируются на опытных данных многих наук.  Основные принципы термодинамики универсальны для живой и неживой природы. Объектами описания в термодинамике являются системы: любая совокупность изучаемых объектов, находящаяся в заданной окружающей среде, может быть названа термодинамической системой. Примерами систем могут вещество, материал, техническое устройство, живая клетка, организм, биосфера, Вселенная. В зависимости от взаимодействия с окружающей (внешней) средой выделяют три вида термодинамических систем, находящихся в устойчивом равновесном (термодинамически стабильном) или неравновесном (установившемся, стационарном и или неустановившемся, переходном) состоянии:

Изолированные системы: не обмениваются с внешней средой ни энергией, ни веществом. Таких систем в реальных условиях не существует, но понятие изолированной системы используют для понимания главных термодинамических принципов.

Закрытые системы: обмениваются со средой энергией, но не веществом. Примером такой системы может служить закрытый термос с налитым в него чаем.

Открытые системы: обмениваются с внешней средой как энергией, так и веществом.

В зависимости от размеров все термодинамические системы подразделяются на макроскопические и малые (микро- и нано)системы.

Состояние любой термодинамической системы определяется (характеризуется) набором термодинамических параметров (физических величин), зависящих (экстенсивные величины) и не зависящих (интенсивные величины) от размеров (объема) системы. Классическая равновесная (техническая и химическая) термодинамика описывает равновесные состояния макроскопических материальных систем и устройств с помощью двух важнейших фундаментальных и универсальных экстенсивных параметров – внутренней энергии U и энтропии S, а также их преобразований (термодинамических потенциалов – свободной энергии Гельмгольца и Гиббса, функций Мессье-Планка), которые являются однозначными (характеристическими) функциями состояния любой системы, зависящими от независимых переменных – экстенсивных (объем и состав) и интенсивных (температура, давление, химический потенциал) параметров состояния, которые можно легко измерять, задавать, контролировать или поддерживать постоянными. При выборе в качестве основных функций состояния внутренней и свободной энергии (энергетический подход) энтропия и функции Мессье-Планка являются экстенсивными независимыми переменными и, наоборот, при выборе в качестве основной функции состояния энтропии и функций Мессье-Планка (энтропиный подход) внутренняя и свободная энергия являются экстенсивными независимыми переменными.

Экстенсивные параметры зависят от размера (объема, массы) системы и могут быть различными в различных частях системы, если она гетерогенная (гетерофазная), а интенсивные – не зависят от размера системы, причем в условиях равновесия они одинаковы во всех ее частях. В качестве независимых переменных состава обычно используются числа молей компонентов , причем в этом случае k – число компонентов равно числу независимых переменных состава, а также их мольные (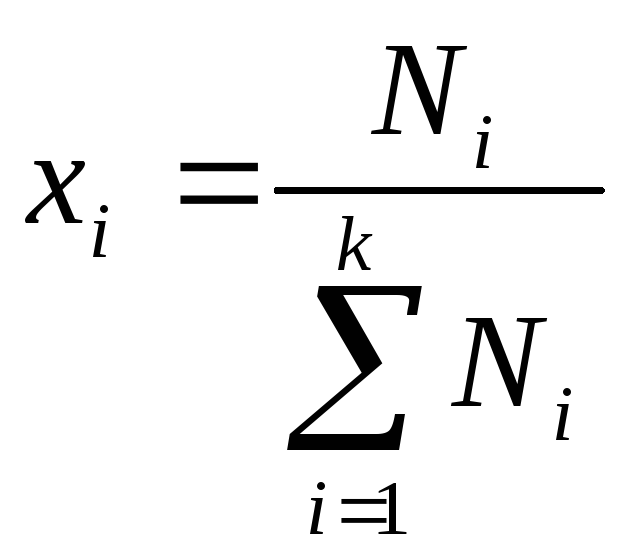), реже удельные (объемные 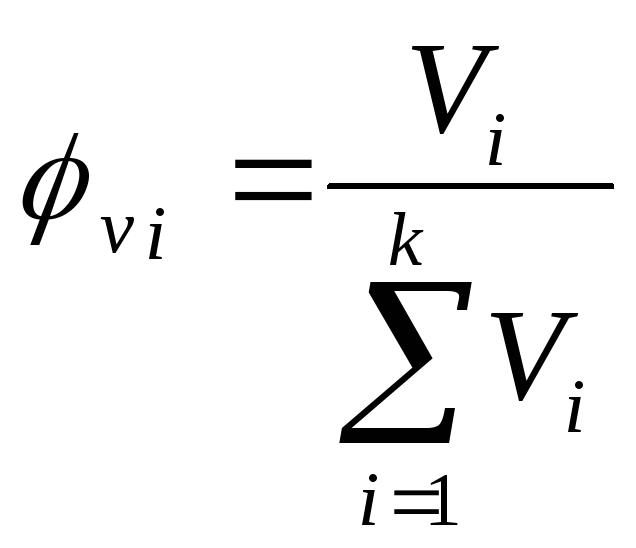и массовые, или весовые 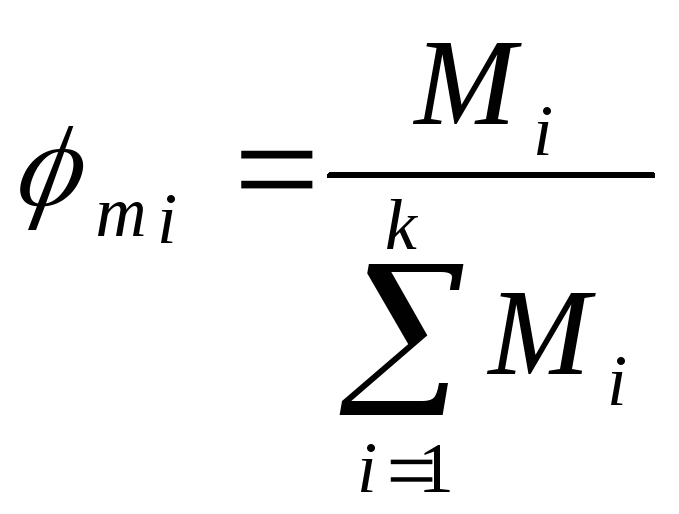) доли. При использовании в качестве переменных состава системы мольных или удельных долей число независимых переменных состава равно k-1, так как общая сумма любых долей равна единице: . При наличии в системе градиентов полей (сил, напряжений или напряженностей) дополнительные независимые переменные выбираются из условий удобства расчетов из сопряженных пар параметров: сила, напряжение или напряженность (интенсивная величина) – реакция на них (экстенсивная величина), т.е., соответственно, механическая сила или напряжение (F или σ) – деформация (Δl или λ),напряженность электрического поля Е – электрическая индукция D, или поляризация Р, диэлектрическая проницаемость ε или восприимчивость χ в диэлектриках, напряженность магнитного поля Н – магнитная индукция В или намагниченность М (магнитная восприимчивость μ) в магнитных системах. При действии в системе гравитационной или центробежной силы и электрического поля в качестве дополнительных интенсивных независимых переменных используются также потенциалы полей тяготения или центробежной силы и электрического поля.

Отношения экстенсивных величин к числу молей компонентов характеризуют их средние и парциальные мольные величины, широко используемые в термодинамике, особенно применительно к многокомпонентным системам. Если обозначить Z как обобщенную экстенсивную величину, то для многокомпонентной системы 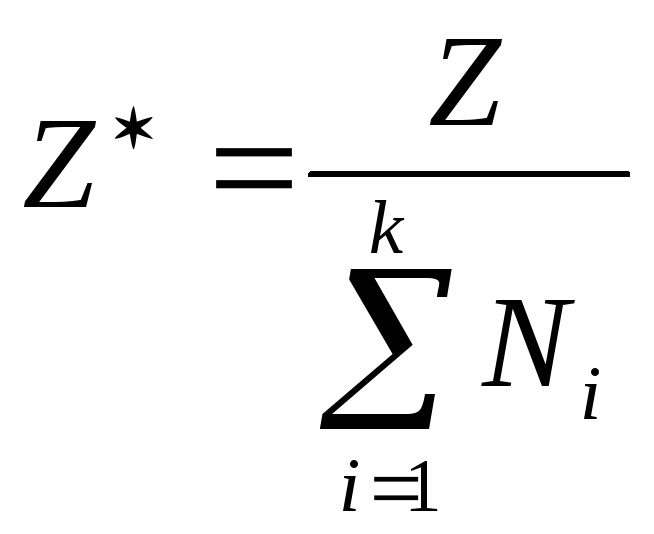является ее средней мольной величиной, а - парциальной мольной величиной. При этом . Для однокомпонентных систем Z* и z представляют собой просто мольные значения экстенсивной величины.

Значения Z, приходящиеся на единицу объема или массы одно- или многокомпонентной системы (удельная объемная и массовая величина - z*_v и z*_m соответственно), также используются в термодинамике, хотя и реже, чем мольные величины, и характеризуют удельные величины, или плотности экстенсивных величин. При этом важно отметить (в отличие от достаточно широко принятых в учебниках представлений), что парциальные мольные и удельные значения экстенсивных величин, хотя и не зависят от размера системы, не являются интенсивными параметрами, так как они не удовлетворяют второму условию их определения - в условиях равновесия они могут иметь неодинаковые значения в разных частях (фазах) гетерофазной системы. Далее будет показано, что исключение составляет химический потенциал μ_i, который формально определяется как парциальная мольная свободная энергия Гиббса и совпадает с мольной свободной энергией Гиббса в случае однокомпонентных систем. Химический потенциал является интенсивной величиной, так как он не только не зависит от размеров системы, но и в условиях термодинамического равновесия одинаков во всех ее частях (фазах). Это обусловлено тем, что химический потенциал в многокомпонентных в гетерогенных системах, имеет более общее значение, чем как парциальная мольная свободная энергия Гиббса, так как он выводится в результате преобразования фундаментального уравнения термодинамики (фундаментального уравнения Гиббса).

Далее коротко даны общие представления об основных функциях состояния и основных соотношениях, связывающих их с независимыми переменными (температурой, объемом, давлением, числом молей при отсутствии внешних сил).