Лабораторная работа № 6. Определение скорости полёта пули

Принадлежности: лабораторная установка, штангенциркуль, ана­литические весы.

Цель работы: ознакомиться с методами определения скорости

полета пули; определить скорость пули одним из

предложенных методов.

Скорость полета пули обычно достигает значительных величин. Поэтому прямое измерение скорости пули требует специальной аппа­ратуры. Много проще проводить измерения косвенными методами (нап­ример, метод вращающихся дисков). Широко распространены методы, использующие неупругие соударения, т.е. соударения, в результате которых столкнувшиеся тела соединяются вместе и продолжают движе­ние как целое.

Пусть летящая пуля испытывает неупругий удар со свободным не­подвижным телом значительно большей массы. После удара тело начи­нает двигаться, причем скорость его во столько раз меньше скорос­ти пули, во сколько раз масса пули меньше массы тела. (Этот ре­зультат легко получить с помощью закона сохранения количества движения.) Если теперь измерить сравнительно небольшую скорость тела, то легко можно вычислить и скорость полета пули.

К числу методов, основанных на этой идее, относят методы бал­листического и крутильного маятников.

I. Метод вращающихся дисков.

Определение скорости полёта пули основано на измерении угла, на который успевают повернуться два бумажных диска, посаженные на вращающуюся с заданной постоянной угловой скоростью ось, за время необходимое пуле для прохождения между этими дисками.

За время t пуля, двигающаяся со средней скоростью V успевает пролететь расстояние

S = Vt (1)

За то же время t диски повернутся на угол

f = wt (2)

где w - угловая скорость вращения. Из (1) и (2)

V = Sw / f (3)

Из пневматической винтовки производится выстрел по неподвиж­ным дискам, пробитые отверстия помечаются. Далее диски приводят в движение с известной угловой скоростью и опыт повторяют. По фор­муле (3) находят скорость полета пули.

II. Баллистический маятник.

Баллистический маятник представляет собой тело массой М под­вешенное на длинных лёгких нитях (рис.1). В маятник стреляют так, чтобы скорость пули была направлена горизонтально по прямой, про­ходящей через центр тяжести маятника и перпендикулярной к его оси вращения. Со стороны выстрела маятник открыт, поэтому пуля, про­никая внутрь, теряет свою начальную скорость и одновременно сооб­щает маятнику некоторый импульс, под действием которого он откло­няется от вертикальной линии на некоторый угол a.

Рассматривая этот процесс как неупругий удар и применяя за­кон сохранения момента количества движения для системы пуля - ма­ятник можно записать:

mV₀l = (ml² + J)w₀ (1)

где m - масса пули, V_o- скорость пули до удара, l - расстоя­ние от оси вращения маятника до его центра тяжести или до точки удара пули, J - момент инерции маятника относительно оси враще­ния, w_o - начальная угловая скорость маятника.

В уравнении (4) левая часть даёт выражение момента количест­ва движения пули относительно оси вращения в начале удара, правая часть выражение момента количества движения маятника вместе с за­севшей в ней пулей также относительно оси вращения после оконча­ния удара.

С другой стороны, применяя к процессу, происходящему в сис­теме после удара, закон сохранения энергии, получим:

(J + ml²) w_o²/ 2 = (M + m) gh (2)

где h - величина поднятия центра тяжести маятника после удара.

Величина может быть определена из измерений отклонения маятника от положения равновесия (рис.1).

Рис.1.

Из рис.1. видно, что

h = l - lcos a = 2lsin²(a/2) (3)

Тогда (2) перепишется так:

(J + ml²) w_o²/ 2 = 2(M + m) glsin²(a/2) (4)

В уравнении (4) левая часть даёт выражение кинетической энергии в первый момент по окончании удара, правая часть даёт вы­ражение потенциальной энергии системы в момент достижения наи­большего отклонения системы. Из уравнения (1), с учетом уравнения (4), находим:

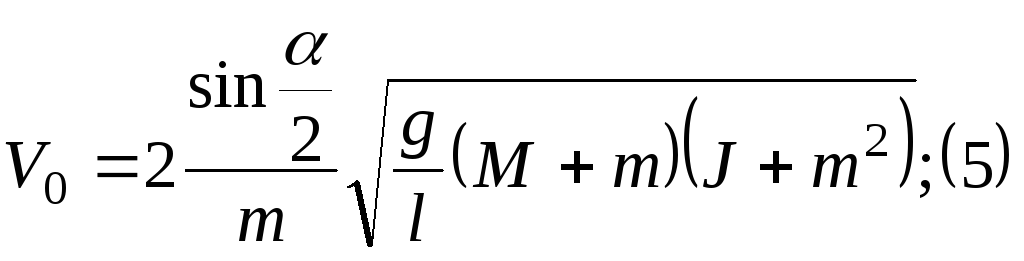
Принимая во внимание то обстоятельство, что размеры маятника малы по сравнению с длиной подвеса, т.е. данный маятник можно рассматривать как математический, легко показать, что уравнение, выражающее закон сохранения момента количества движения переходит

в уравнение, выражающее закон сохранения количества движения. К

тому же можно взять , тогда (8) значительно упрощается,

и мы приходим к окончательной формуле для определения скорости V₀

_{полёта пули}

Величины в этой формуле: M, m, a, l - находятся из измерений, Q = 2lsin(a/2) - смещение.

ИЗМЕРЕНИЯ

1. Производится не менее 5 выстрелов по мишени.

2. Результаты заносятся в таблицу 2.

3. Оценить ошибку измерений

Таблица 2.

N	M	m	Q	L	V