Решение типового варианта индивидуального задания №3.
Задача
№1.
Найти неопределённый интеграл
Решение: Применим формулу интегрирования по частям
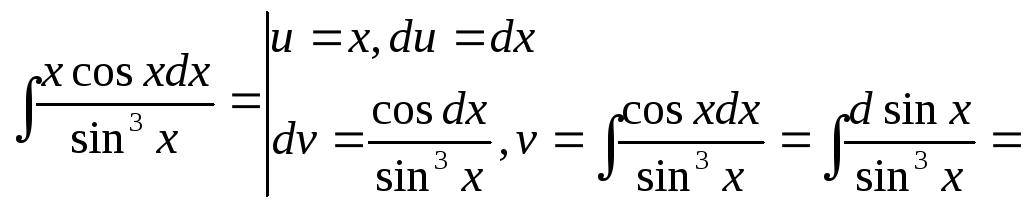
Ответ:
Задача
№2.
Найти неопределённый интеграл
Решение: Применим метод замены переменной
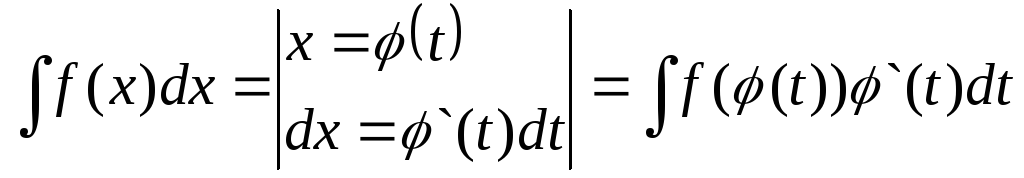
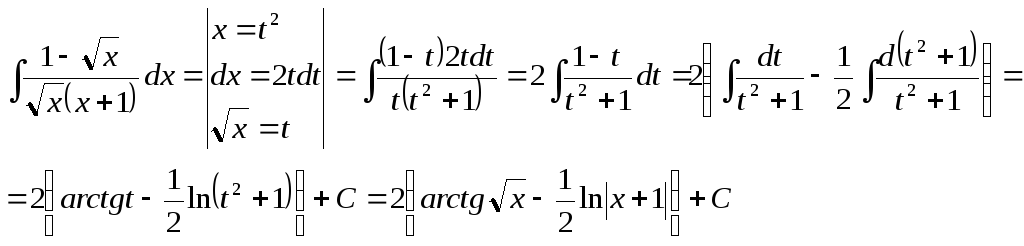
Ответ:
Задача
№3.
Найти неопределённый интеграл
Решение: Так как старшие степени многочленов в числителе и знаменателе дроби равны, то нужно выделить целую часть дроби. Сначала выполним умножение в знаменателе, записав многочлен по убывающим степеням х.
x(x+4)(x-2)=x(x2+4x-2x-8)=x(x2+2x-8)=x3+2x2-8x
Теперь разделим числитель дроби на знаменатель
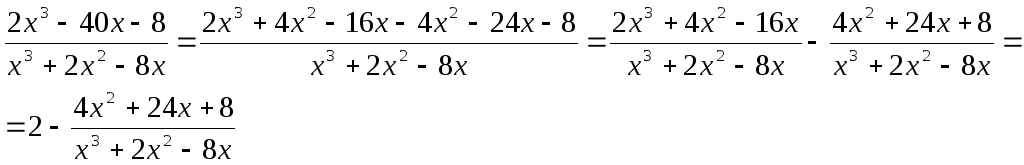Таким
образом имеем
Теперь разложим
дробь
на сумму дробей
,
где А, В, С – неопределённые коэффициенты.
.
Приравниваем
коэффициенты при одинаковых
х, получим систем
уравнений
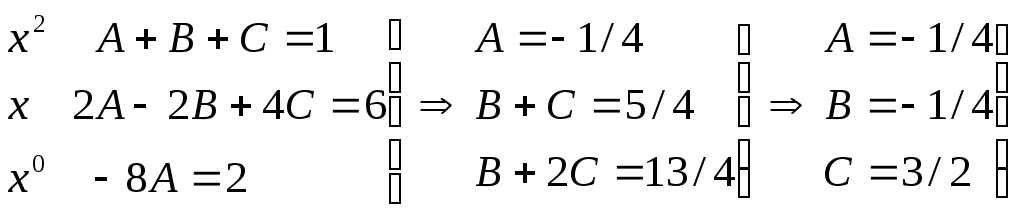
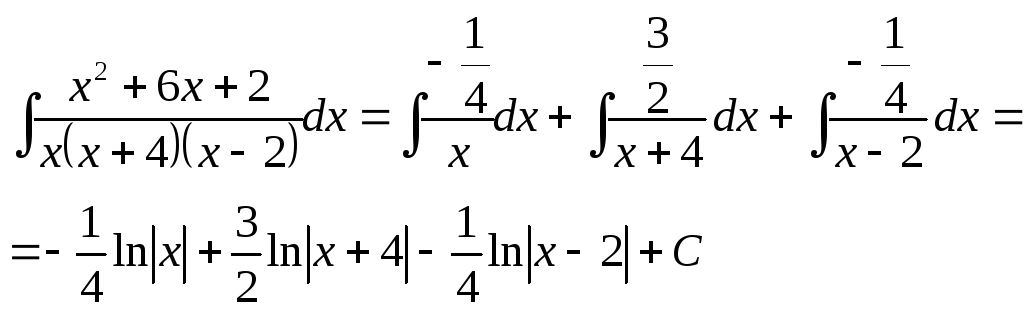
Ответ:
Задача №4. Найти неопределённый интеграл
Решение: Дробь под знаком интеграла правильная, так как старшая степень многочлена в числителе меньше старшей степени многочлена в знаменателе (4). Разложим дробь на сумму простых дробей
имеем
x3+6x2+13x+6=A(x3+6x2+12x+8)+B(x3+2x2-4x-8)+C(x2-4)+D(x-2) Приравниваем коэффициенты при одинаковых х, получим систем уравнений
→
→
→
→
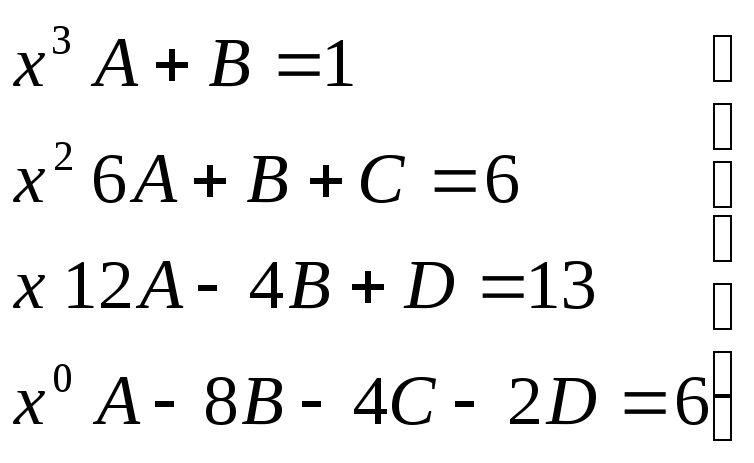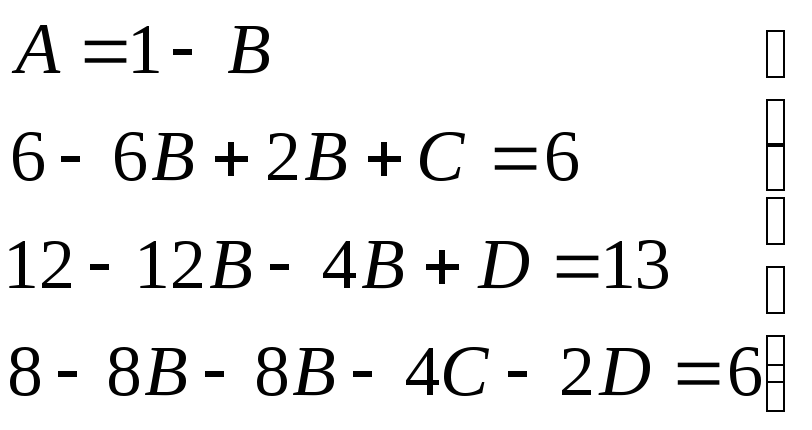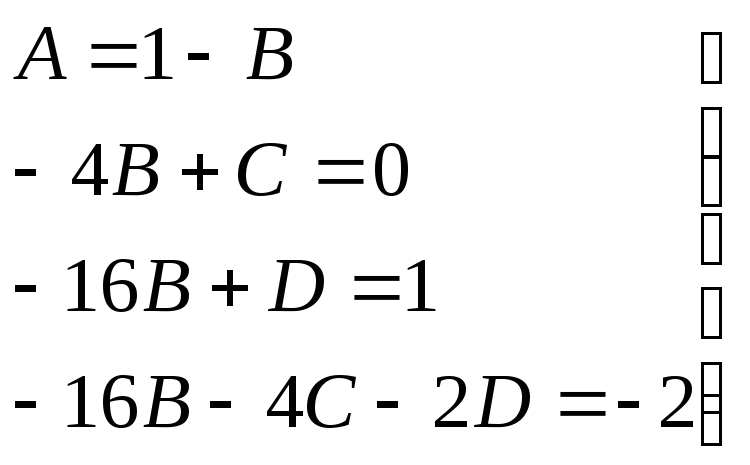
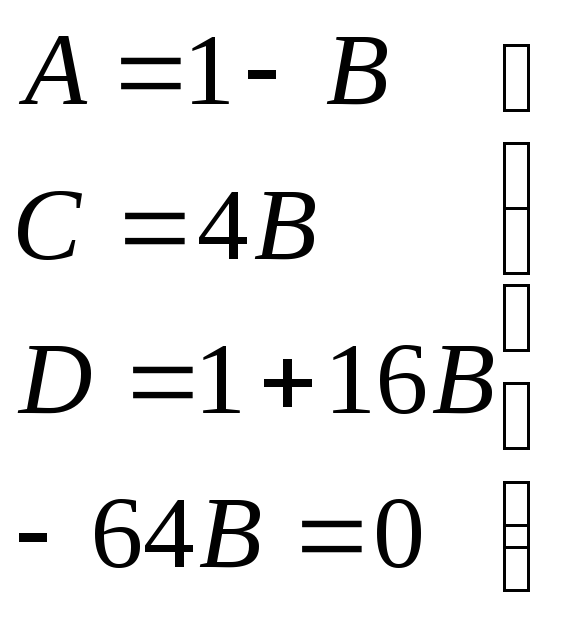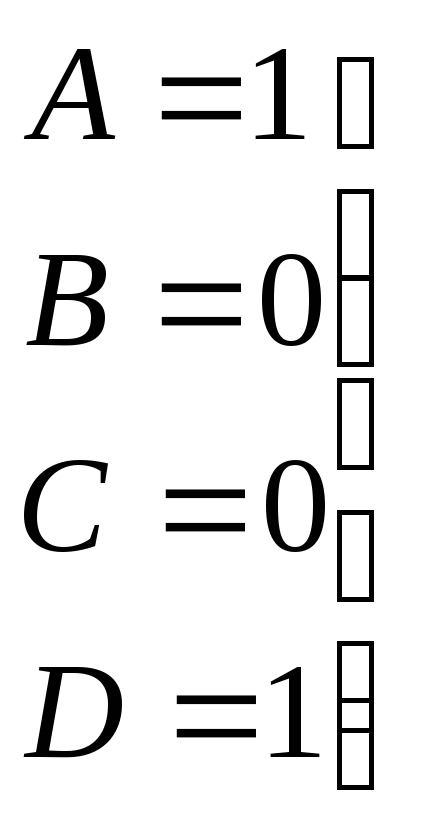
Итак,
Ответ:
Задача
№5.
Найти неопределённый интеграл
Решение: Дробь под знаком интеграла правильная, поэтому представим её как сумму простых дробей.
;
получим
(Ax+B)(x2+1)+(Cx+D)(x2+x+1)=2 x3+3 x2+3x+2
Ax3+Bx2+Ax+B+Cx3+Dx2+Cx2+Dx+Cx+D=2 x3+3 x2+3x+2
Приравниваем
коэффициенты при одинаковых
х, получим систем
уравнений
→
→
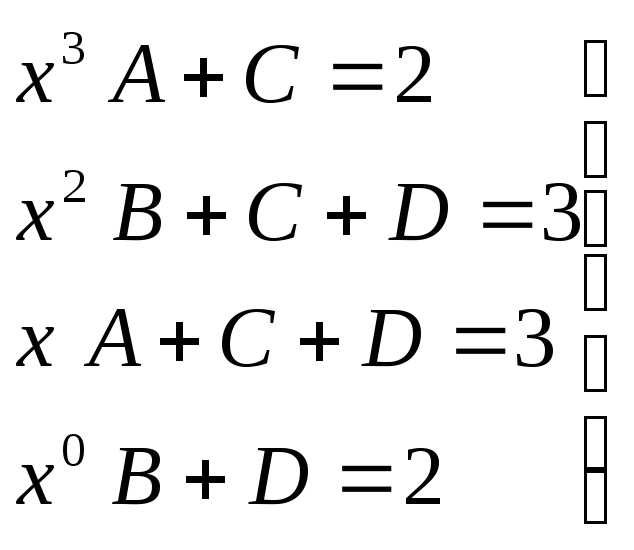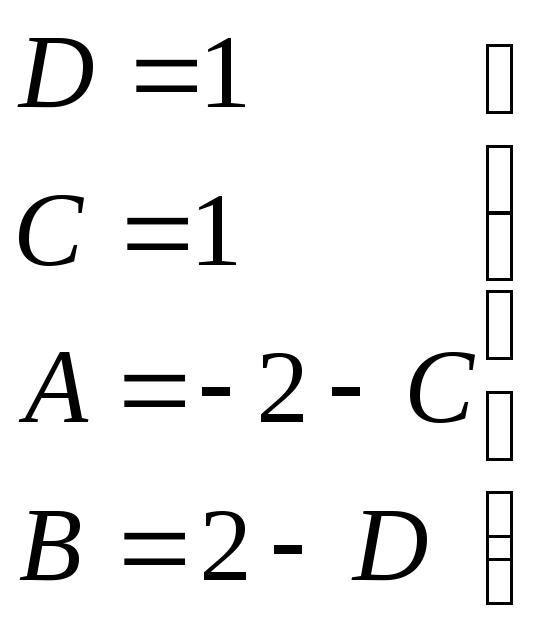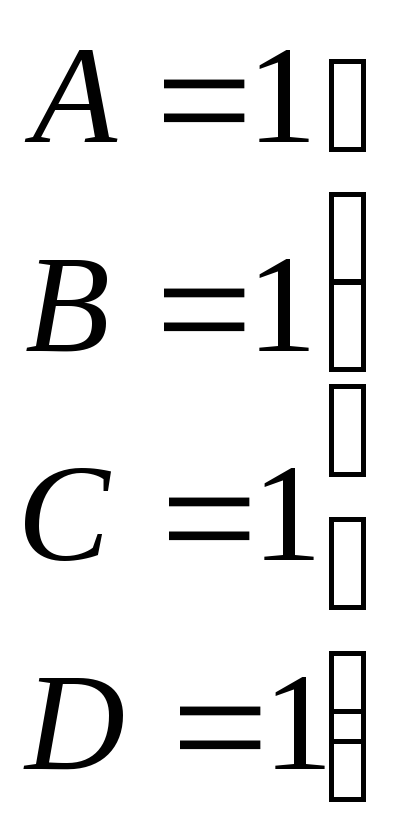
Таким образом получим
Первый из полученных
интегралов вычисляем так: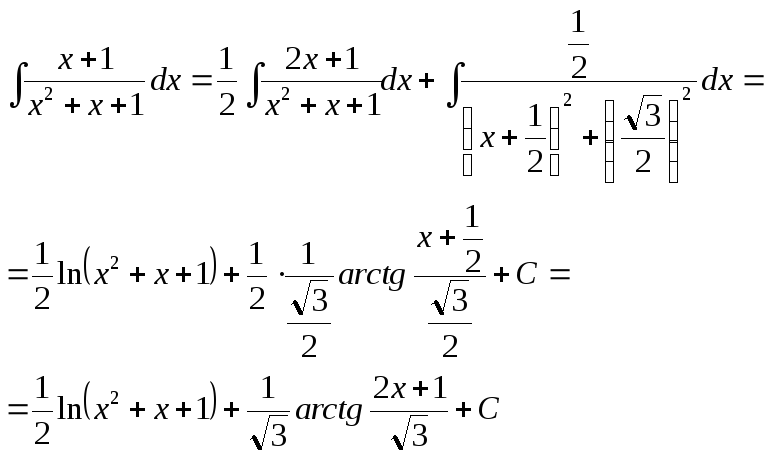
Второй интеграл будет вычислен так:
Ответ:
Задача
№6.
Вычислить определённый интеграл
Решение:
Перепишем интеграл в виде
и применим третью подстановку при
интегрировании дифференциального
бинома
так как у нас р=1/5, m=-7/5,
n=1/3 и
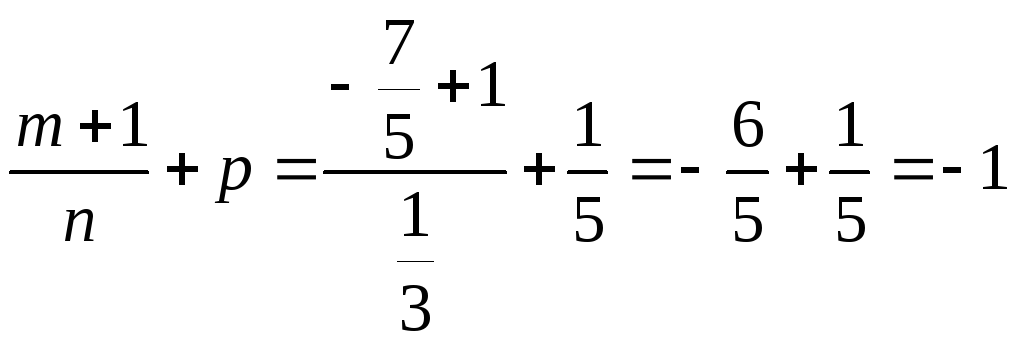- целое поэтому
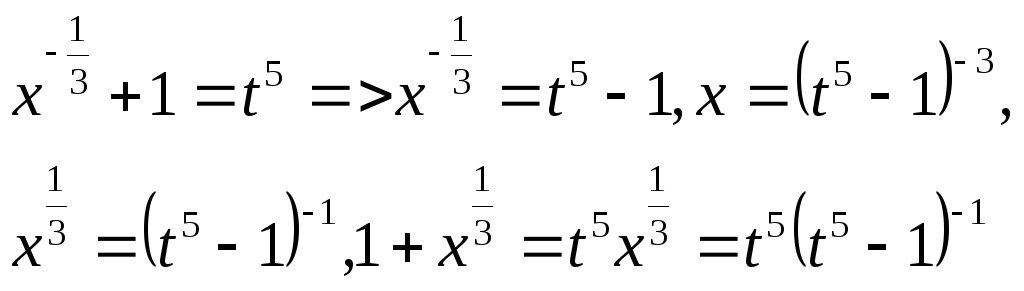
dx=-3(t5-1)-45t4dt=-15t4(t5-1)-4dt
Таким
образом
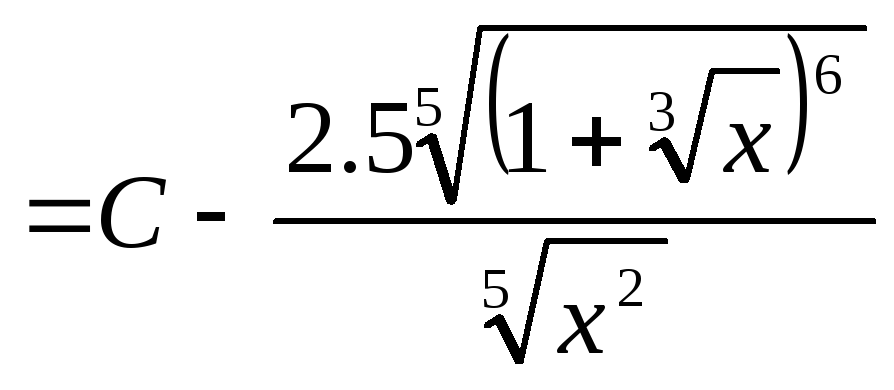
Ответ:
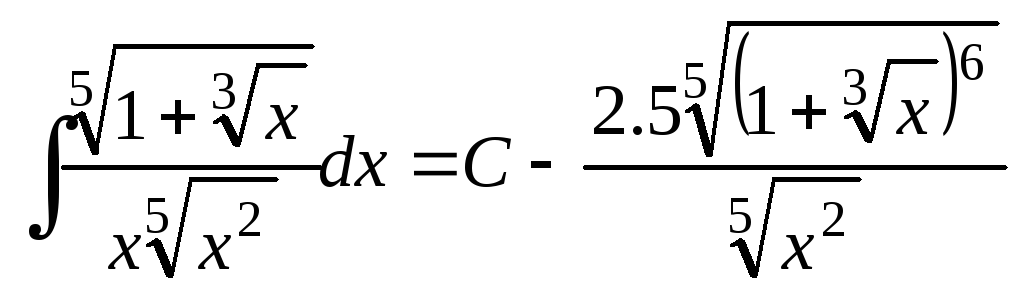
Задача
№7.
Вычислить определённый интеграл
Решение:
Применим формулу интегрирования по
частям в определённом интеграле
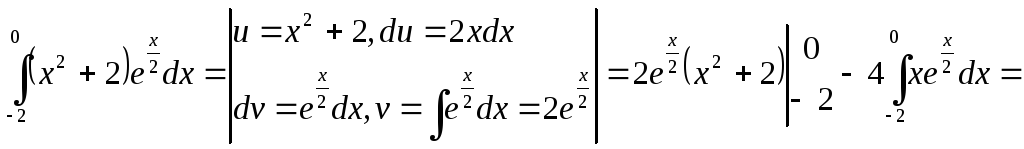
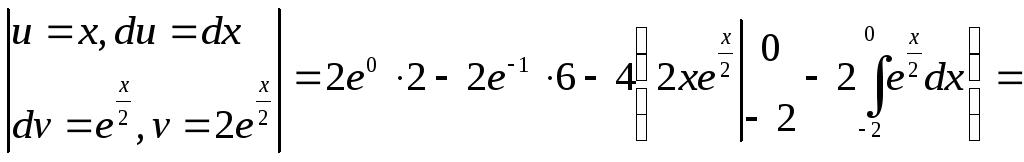
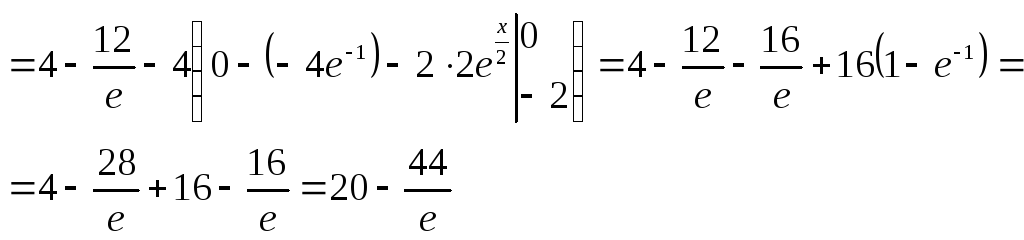
Ответ:
Задача
№8.
Вычислить определённый интеграл
Решение: Применим метод замены переменной в определённом интеграле
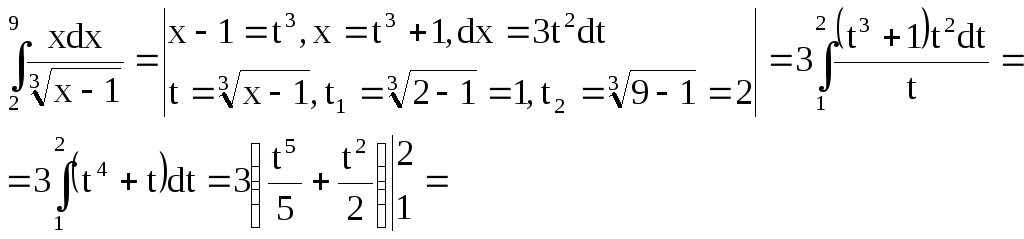
Задача
№9.
Вычислить определённый интеграл
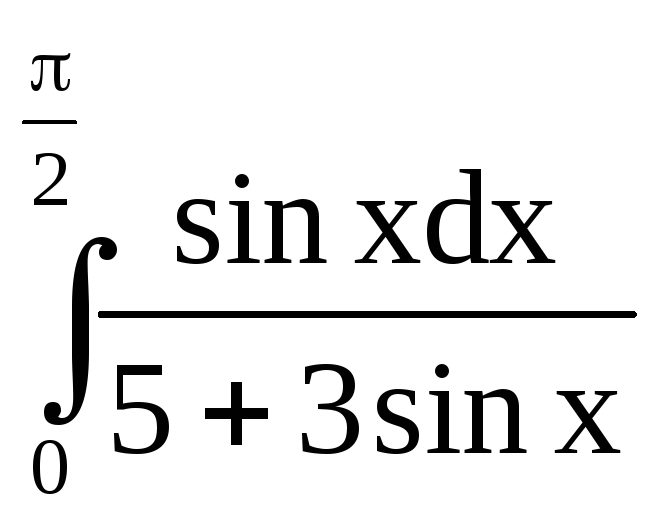
Решение:
Вычислим определённый интеграл,
применяя метод замены переменной, а
именно, универсальную подстановку
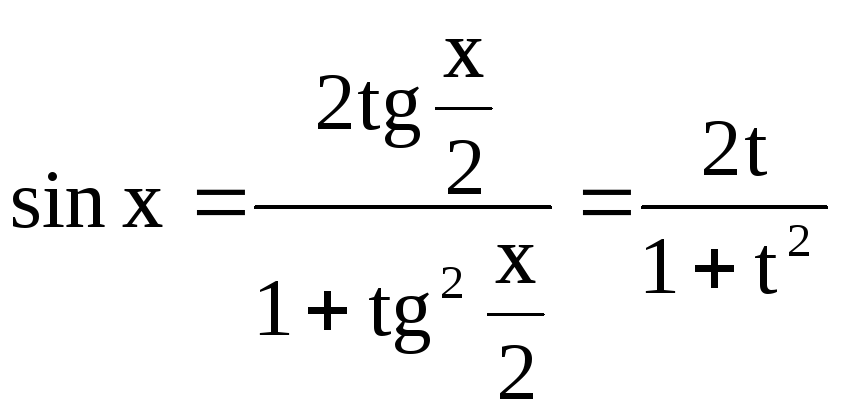
Таким образом
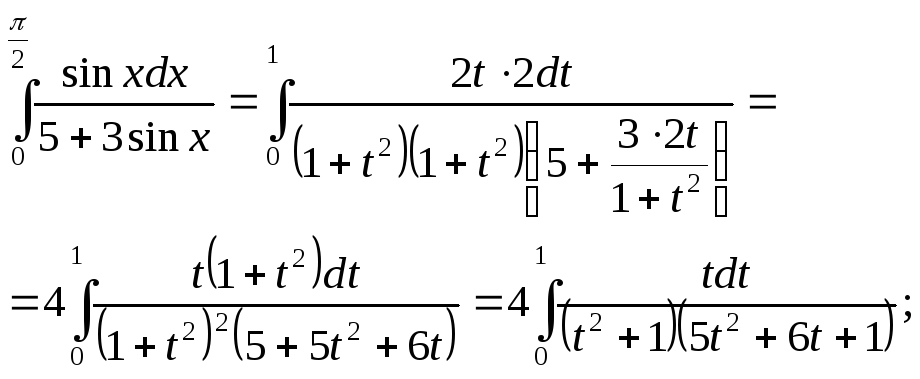
Вычислим сначала
неопределённый интеграл
(At+B)(5t2+6t+1)+(Ct+D)( t2+1)=t
→
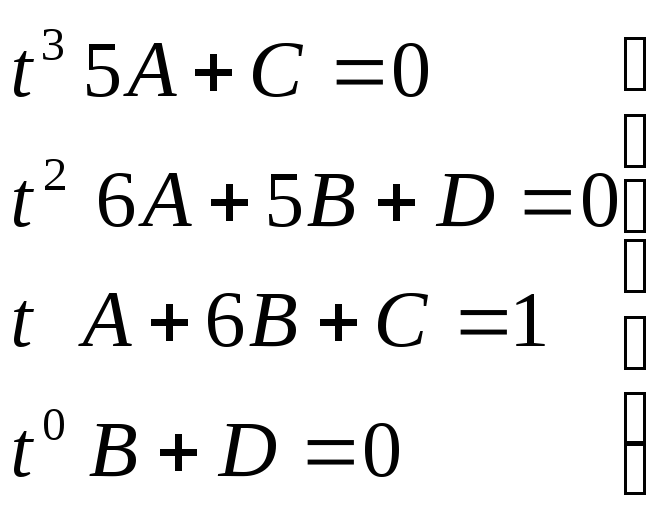из (1) => C=-5A; (2)-(4)=> 6A+4B=0 =>B=-1.5A; из (4) => D=-B => D=1.5A.
Тогда в уравнении (3) имеем:
A-6∙1.5A-5A=1
=> A-9A-5A=1 => -13A=1 => A=
=> C=
,
B=
,
D=
.
=
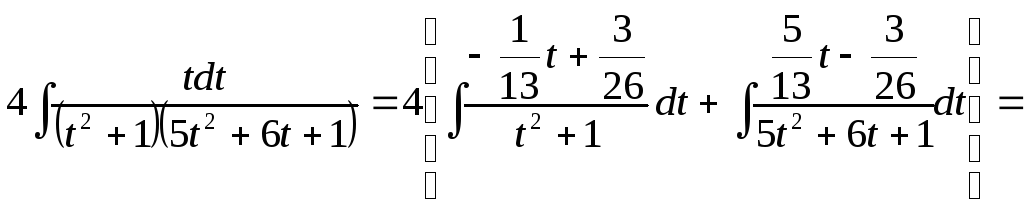
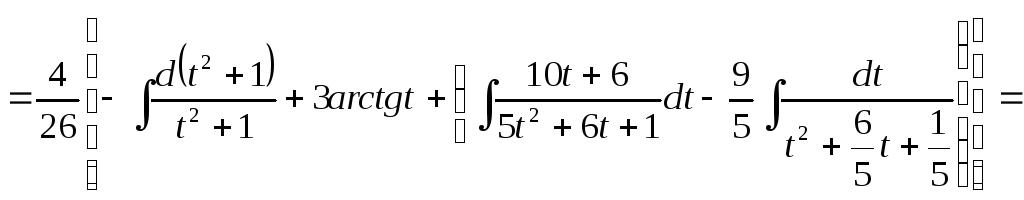
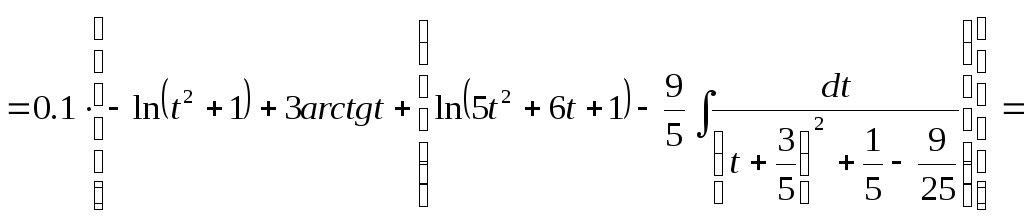
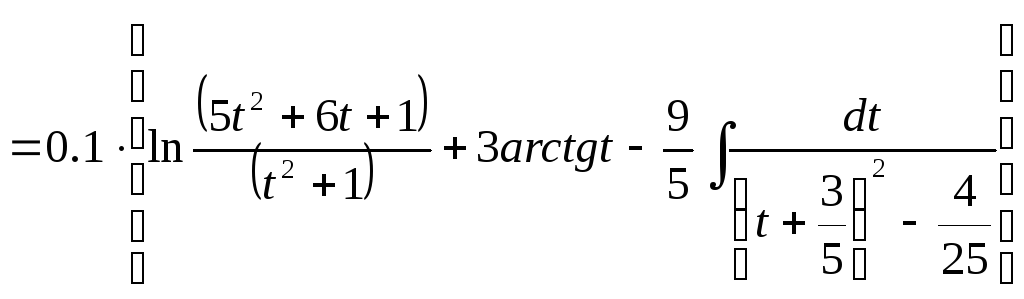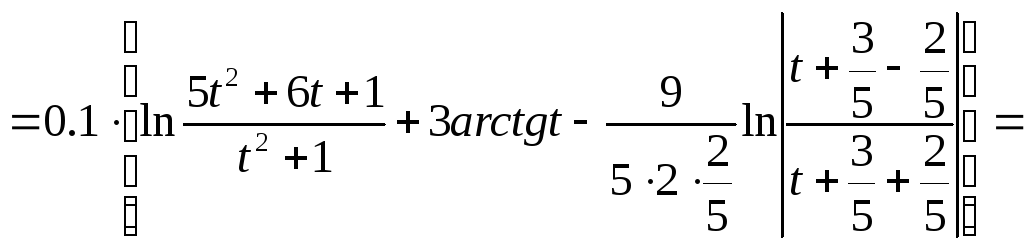
Теперь остаётся вычислить определённый интеграл
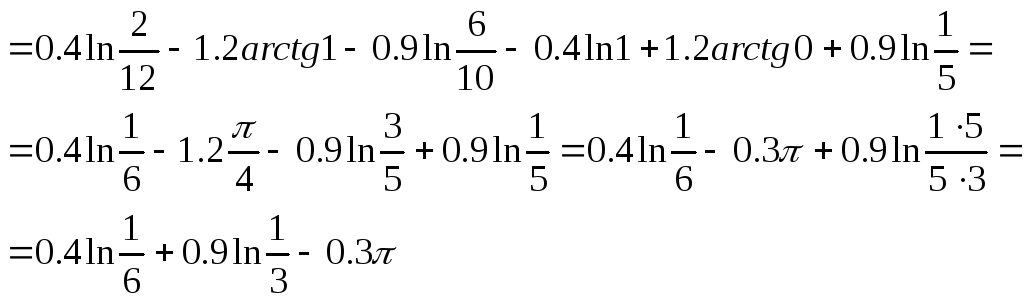
Ответ:
Задача
№10.
Вычислить определённый интеграл
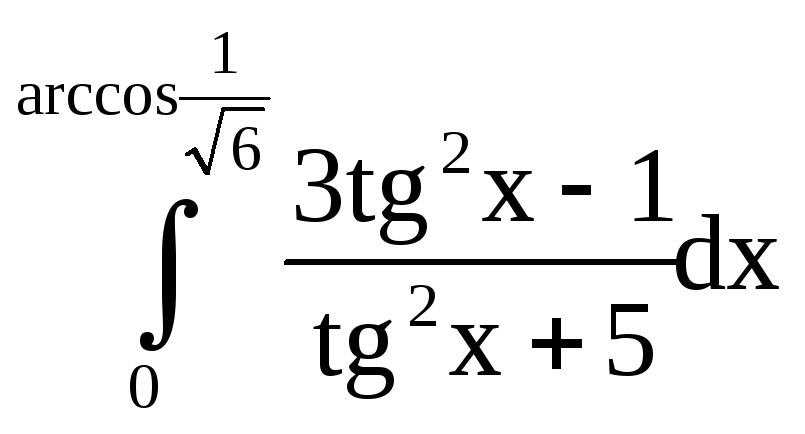
Решение: Вычислим интеграл, применяя метод замены переменной.
Пусть
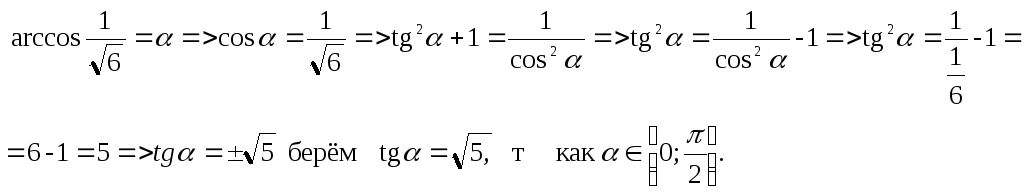Замена переменной
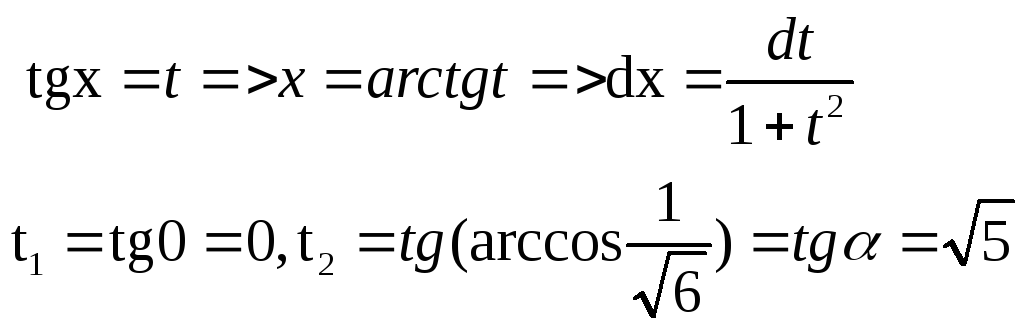
Таким образом
,
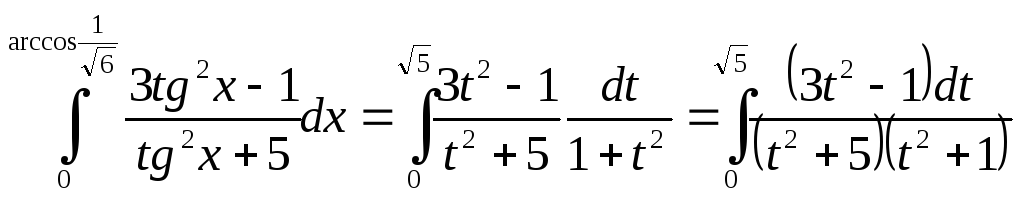Вычислим сначала неопределённый интеграл, а потом воспользуемся формулой Ньютона – Лейбница
(At+B)(t2+1)+(Ct+D)(t2+5)=3t2-1
Приравниваем
коэффициенты при одинаковых
t,
получим систем уравнений
→
→
→
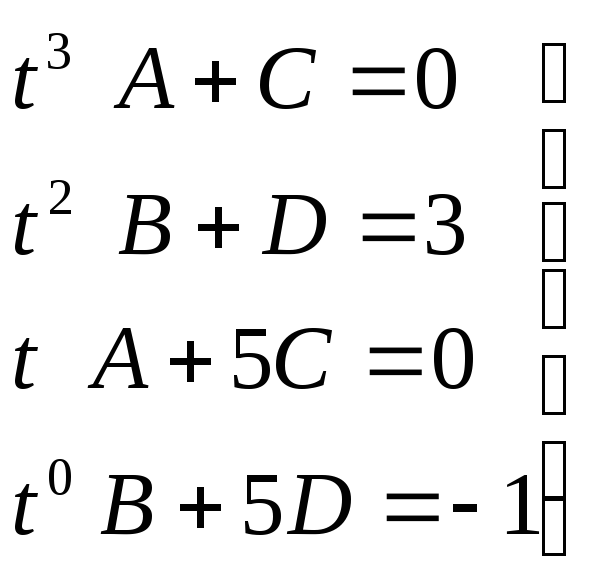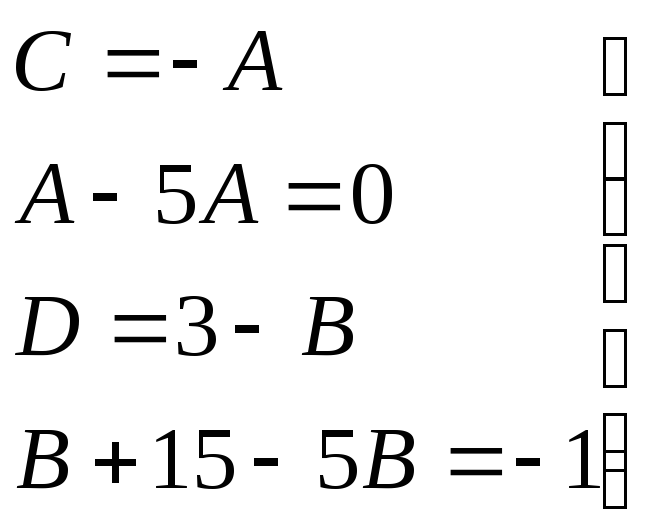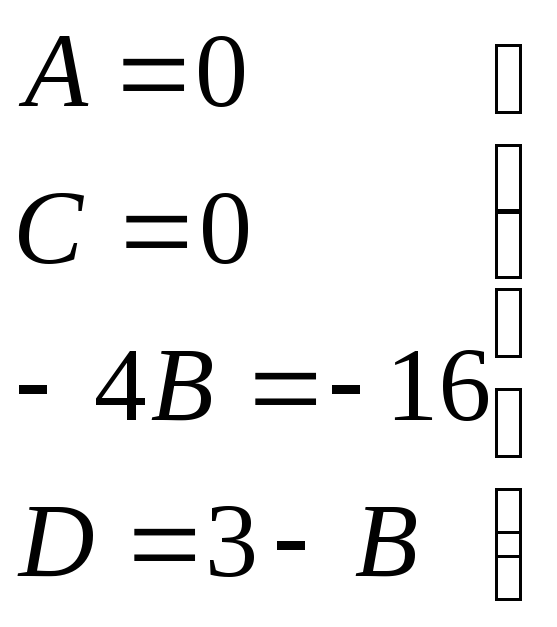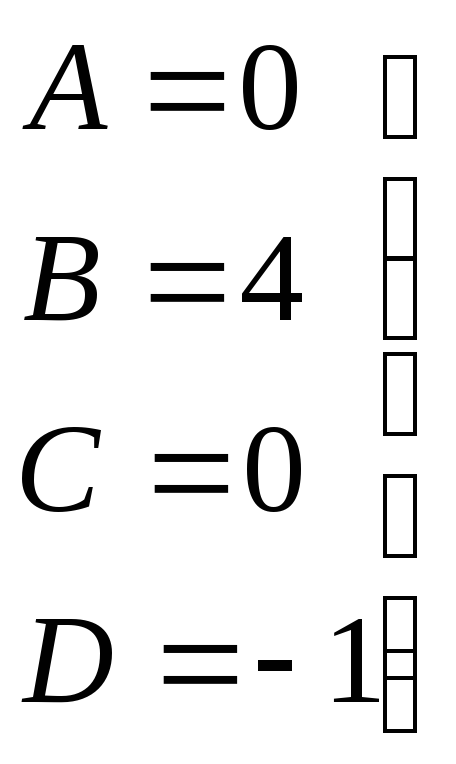
Ответ: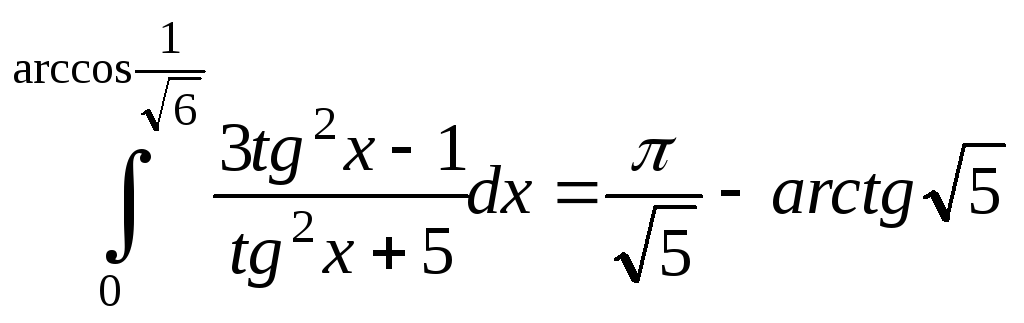
Задача
№11.
Вычислить определённый интеграл
Решение:
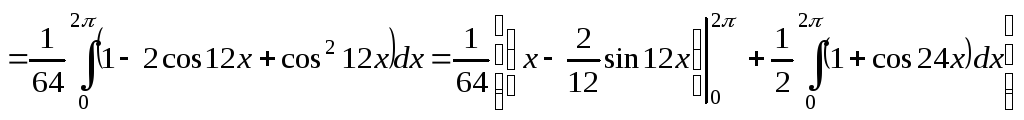
Ответ:
Задача №12. Вычислить определённый интеграл
Решение:
Вычислим интеграл, применив метод
замены переменной, предварительно
разделив числитель и знаменатель дроби
на
,
будем иметь
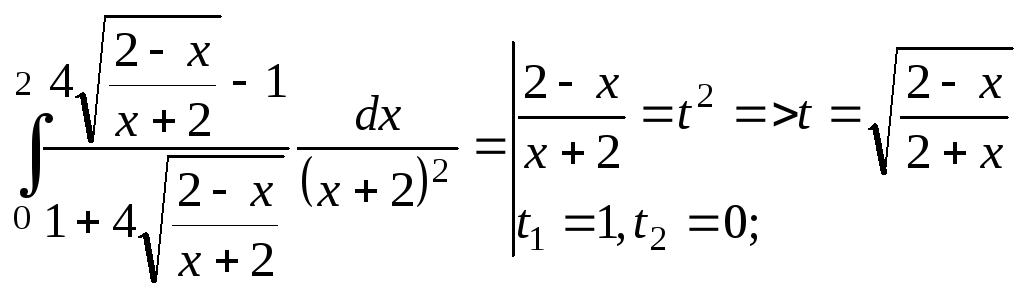
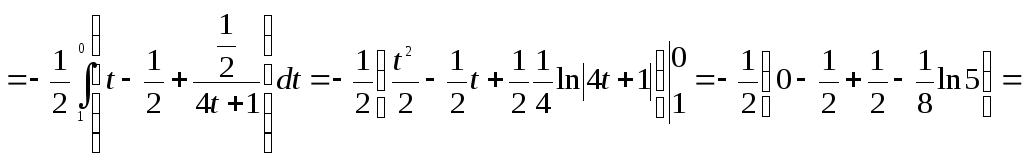
Ответ:
Задача
№13.
Вычислить определённый интеграл
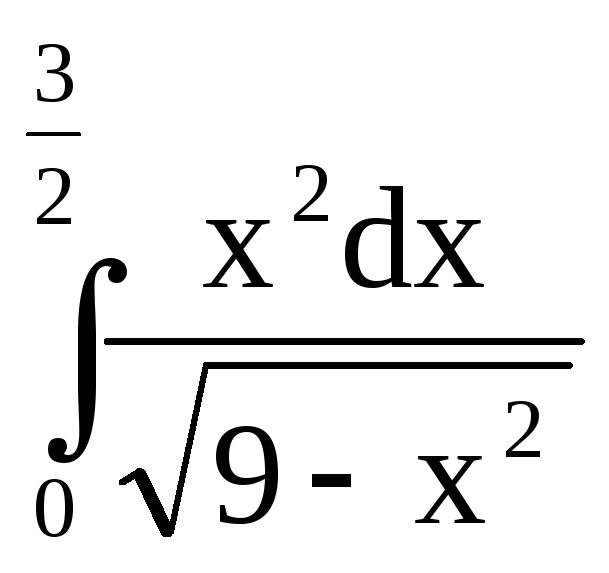
Решение: Применим метод замены переменной
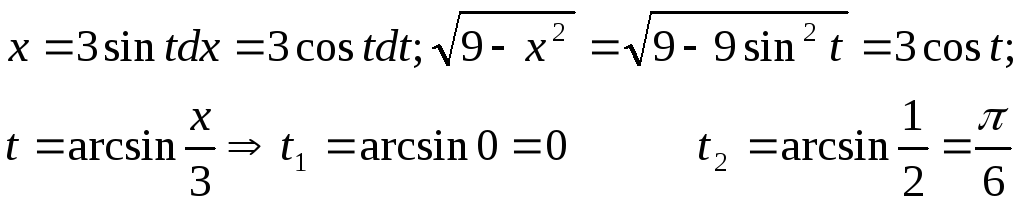
Таким образом
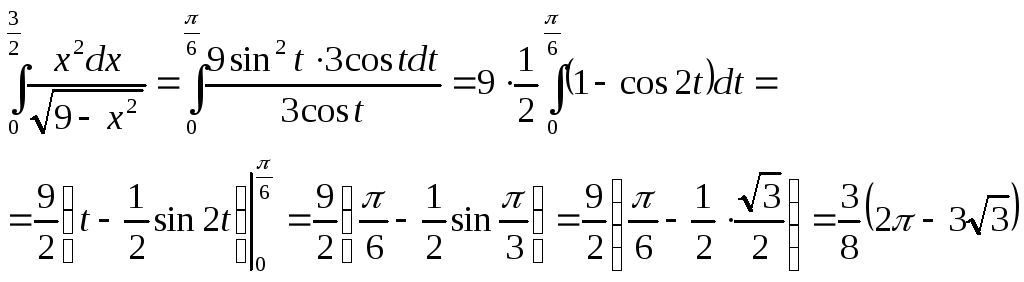
Ответ:
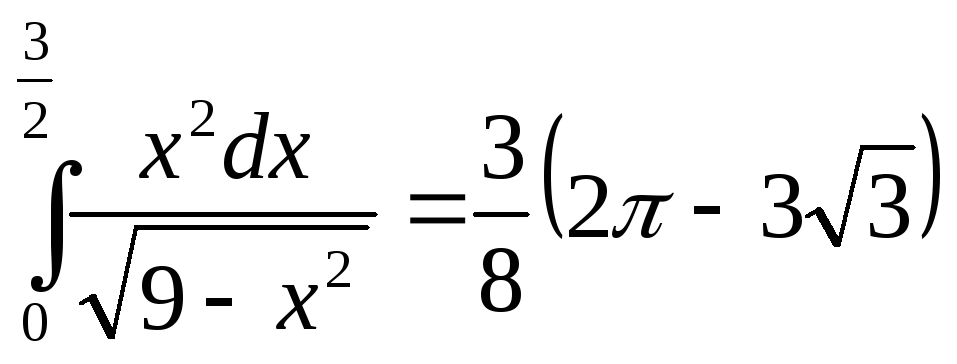
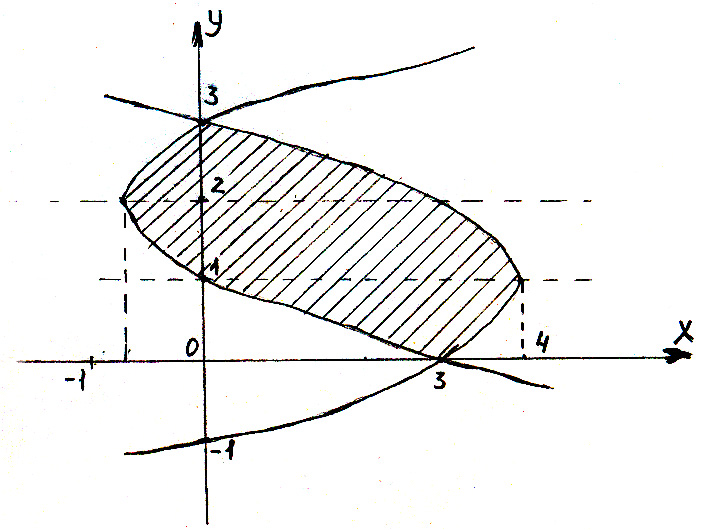
Задача №14. Вычислить площадь фигуры, ограниченной графиками функций x=4-(y-1)2, x=y2-4y+3
Решение: Графиками функций являются параболы (y-1)2=-(x-4)- вершина в точке (4,1), ось симметрии у=1, ветви параболы направлены влево от вершины х=у2-4у+3 => =(y-2)2-1 => (y-2)2=x+1 – вершина в точке (-1,2), ось симметрии у=2, ветви направлены вправо от вершины. Найдём точки пересечения парабол с осями координат:
Итак, у
парабол есть общие точки – точки
пересечения (3,0) и (0,3) Искомая площадь
вычисляется так:
(кв.ед).
Ответ: S=15(кв.ед)
Задача
№15.
Вычислить площадь фигуры,
ограниченной линией
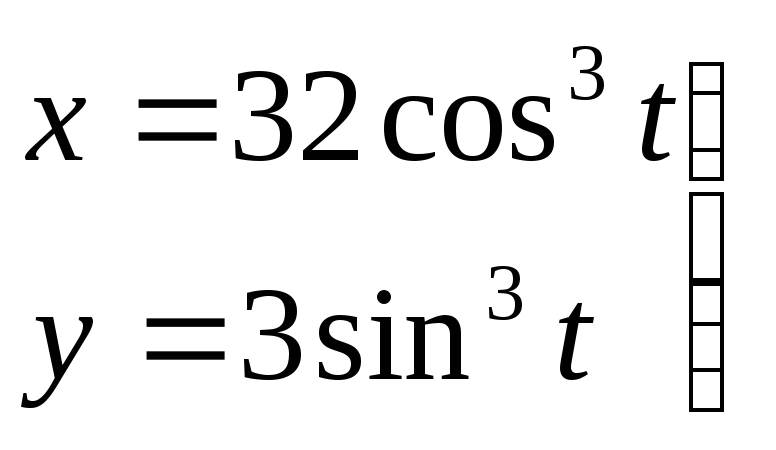
Решение: Линия, задаваемая уравнениями, является астроидой, симметричной относительно осей координат
Приравниваем
;
Эскиз фигуры без
точного соблюдения масштаба приводится.
При нахождении площади фигуры используем
формулу
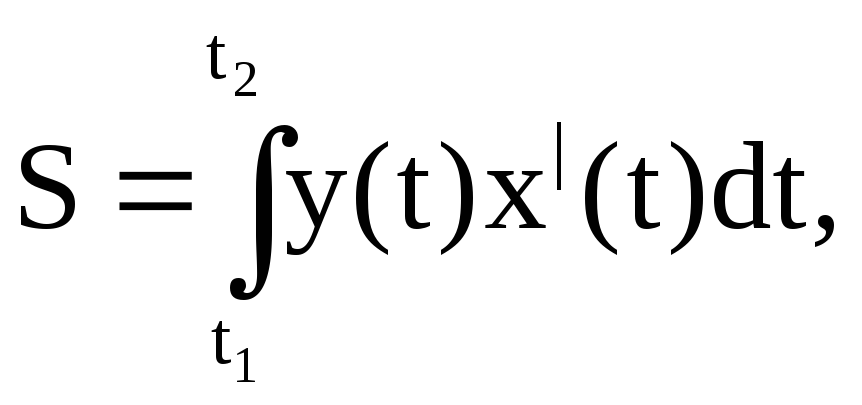у нас
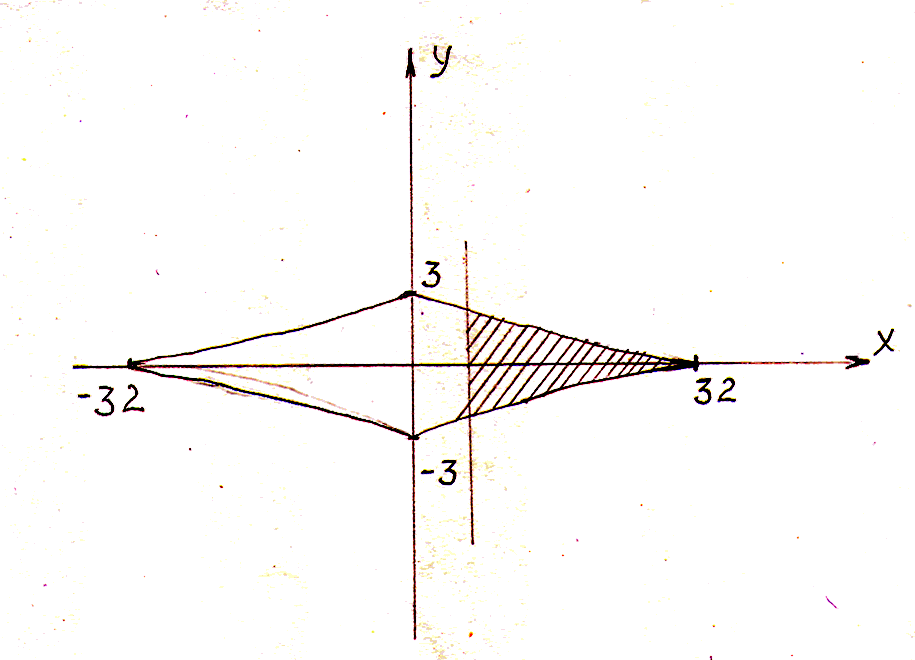
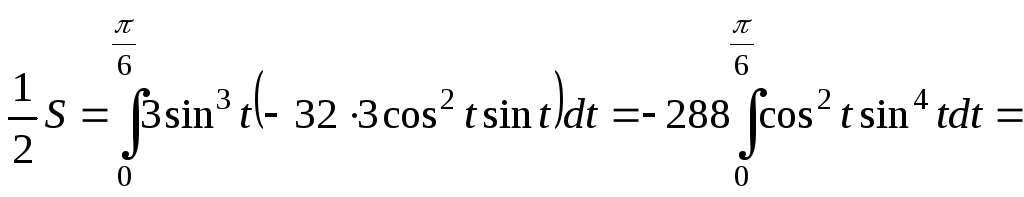
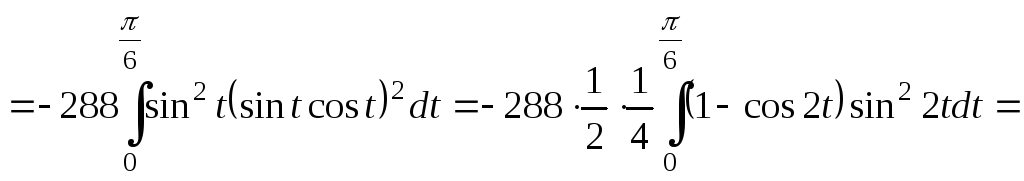
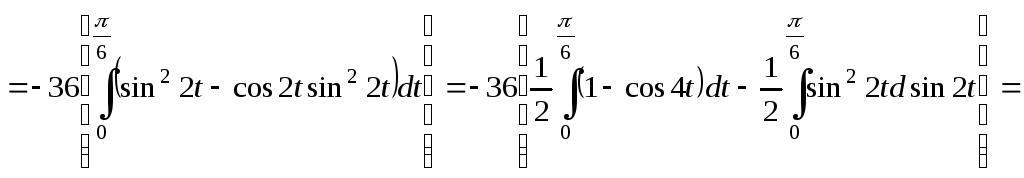
Результат получился
отрицательный потому, что при
Поэтому
Ответ:
(кв.ед.)
Задача
№16.
Вычислить площадь фигуры,
ограниченной линиями, заданными в
полярных координатах.
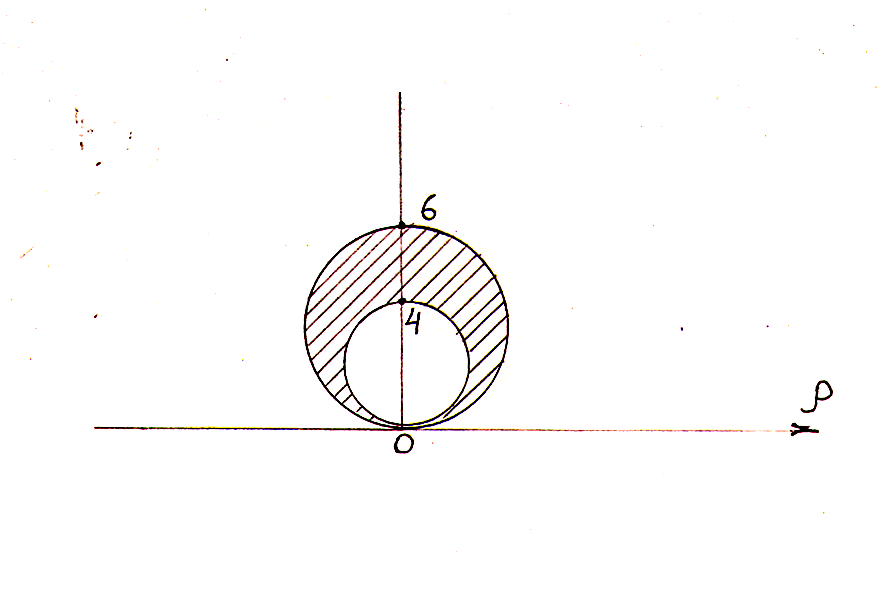
Решение:
Область определения данных функций
≥0,
т.е. sin
≥0
=> 2πk≤φ≤π+2kπ,
при k=0 получим 0≤φ≤π.
Искомая площадь выразится формулой:
у нас α=0, β=π,
ρ2=6sinφ,
ρ1=4sinφ
(кв.ед.)
Ответ: 5π (кв.ед.)
Задача
№17.
Вычислить длину дуги кривой,
заданной уравнением
0 ≤ х ≤ 3
Решение: Воспользуемся формулой вычисления длины дуги кривой:
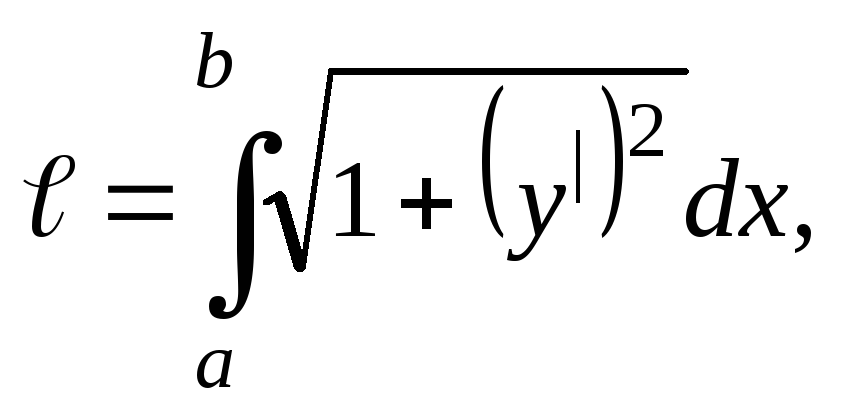у нас а=0, b=3,
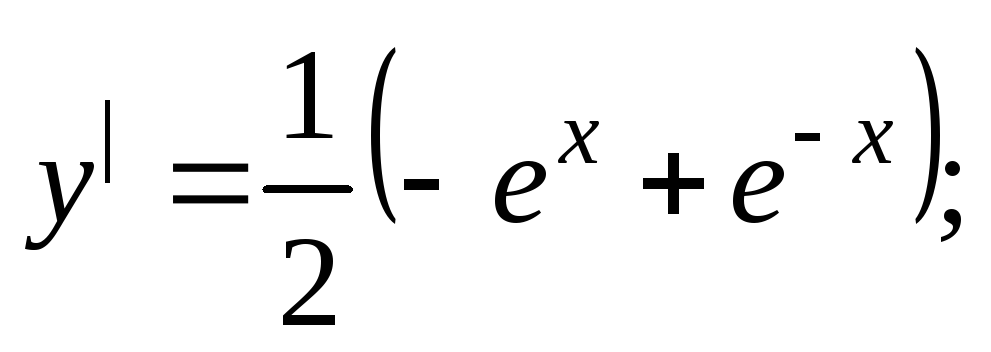
(лин.ед.)
Ответ:
(лин.ед)
Задача
№18. Вычислить
длину дуги кривой, заданной
параметрическими уравнениями
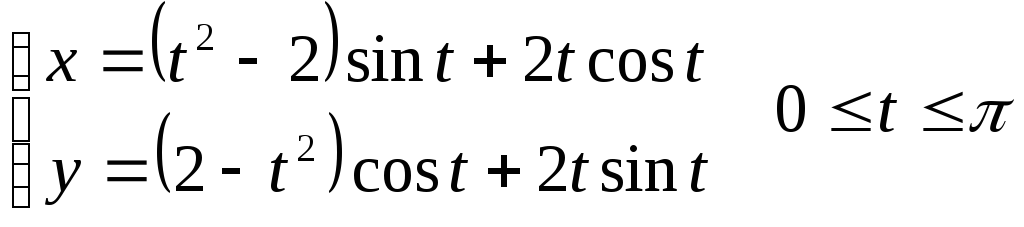
Решение: Воспользуемся формулой вычисления длины дуги кривой:
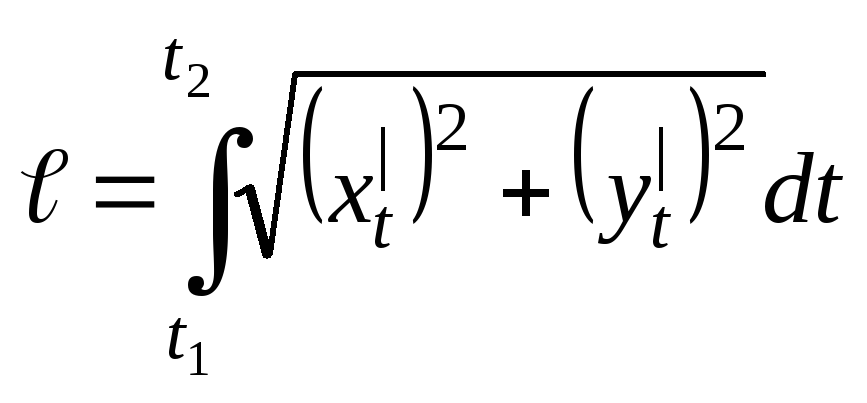у нас
t1=0,
t2=π
x| = 2tsin t + (t2-2)cos t+2cos t-2tsint =t2cos t
y| = -2tcos t - (2-t2)sin t+2sin t+2tcost =t2sin t
(лин.ед)
Ответ:
(лин.ед)
Задача
№19.
Вычислить длину дуги
кривой, заданной в полярной системе
координат ρ=6sinφ, 0≤φ ≤
Решение:
Воспользуемся
формулой
,
у нас α=0, β=
,
ρ|=6cosφ, поэтому
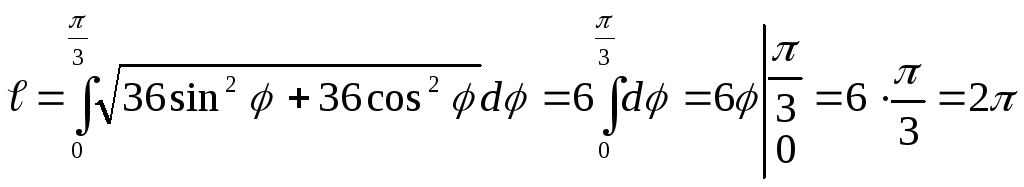
Ответ:
(лин.ед.)
Задача №20. Вычислить объём тела, ограниченного поверхностями:
z=7,
z=0
Решение: В данной задаче задан эллипсоид (а=4,b=3,с=14), координатная плоскость ОХУ (z=0) и плоскость, ей параллельная, z=7 Рассекая эллипсоид плоскостью, параллельной ОХУ на расстоянии z от нее (0≤ z ≤7), получим эллипс
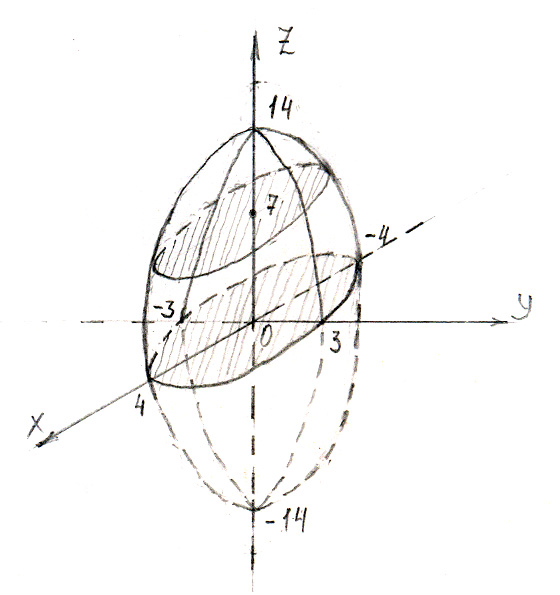
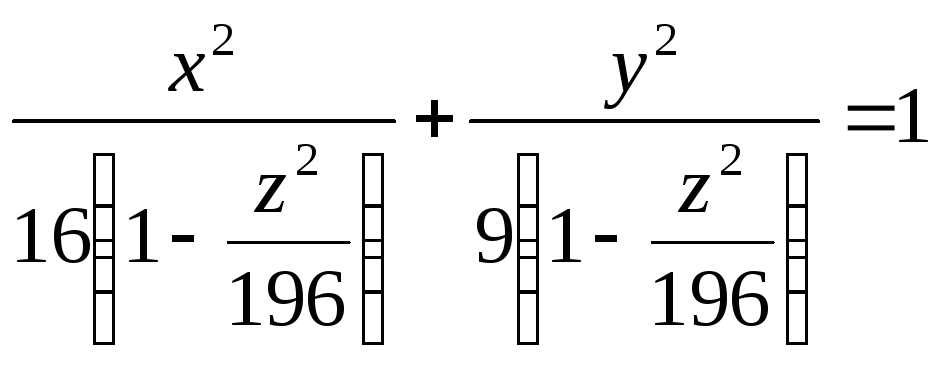или
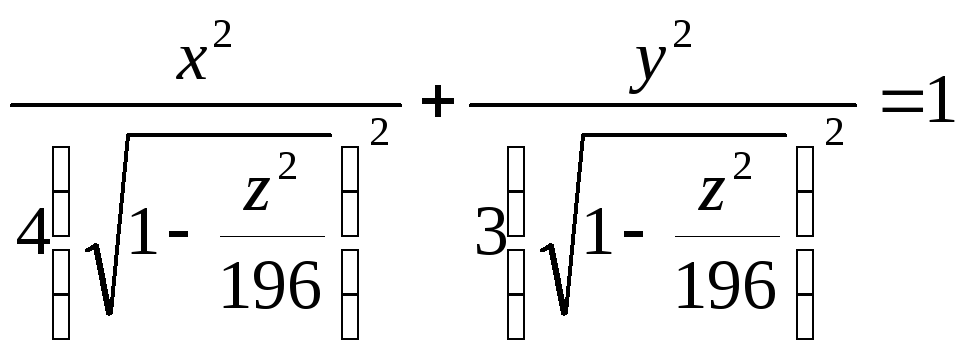
Напомним, что
площадь эллипса равна произведению
значений его полуосей на число π, т.е.
если уравнение эллипса имеет вид
=> S=πab. У
нас
=>
Применим формулу вычисления объёма тела по известной площади параллельного сечения:
В нашей задаче
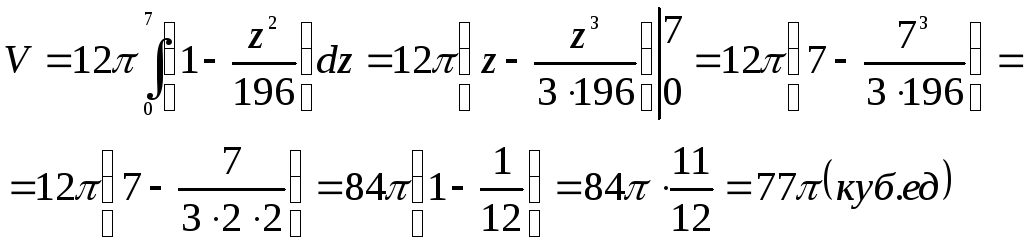
Ответ:
(куб.ед.)