Министерство образования и науки Российской федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

53 № 3388

К 602

КОЛЕБАНИЯ И ВОЛНЫ

Лабораторный практикум по курсу общей физики для студентов I–II курсов РЭФ, ФЭН, ФТФ, ИДО всех направлений подготовки и всех форм обучения

Новосибирск 2007

УДК 534(07)

         К 602

Составители: канд. физ.-мат. наук, доц. В.Ф. Ким,

канд. физ.-мат. наук, доц. Э.А. Кошелев,

канд. физ.-мат. наук, доц. Ю.Е. Невский

Рецензент: канд. физ.-мат. наук, доц. И.И. Суханов

Работа подготовлена на кафедре прикладной и теоретической физики НГТУ

 Новосибирский государственный технический университет, 2007   

Колебания и волны лабораторный практикум

Редактор И.Л. Кескевич

Выпускающий редактор И.П. Брованова

Компьютерная верстка В.Ф. Ноздрева

Подписано в печать 11.09.2007. Формат 6084 1/16. Бумага офсетная. Тираж 500 экз. Уч.-изд. л. 2,79. Печ. л. 3,0. Изд. № 159. Заказ № . Цена договорная

Отпечатано в типографии Новосибирского государственного технического университета 630092, г. Новосибирск, пр. К. Маркса, 20

Работа № 20а

Свободные колебания физического маятника

Цель работы: исследовать зависимость периода колебаний физического маятника от положения оси вращения, относительно которой происходит качание маятника; используя полученную экспериментальную зависимость, определить моменты инерции тела относительно оси, проходящей через центр инерции, и относительно других осей, параллельных первой.

Дифференциальное уравнение колебаний физического маятника

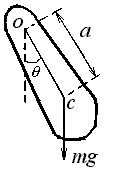
Физический маятник – твердое тело, которое может вращаться под действием силы тяжести вокруг неподвижной горизонтальной оси, проходящей через точку , не совпадающей с точкой центра инерции этого тела. Схема маятника показана на рис. 1.

Д

Рис. 1

ифференциальное уравнение колебаний (уравнение движения) физического маятника можно получить из закона сохранения энергии. В состоянии равновесия потенциальную энергию маятника относительно Земли будем считать равной нулю. Тогда при отклонении маятника на угол потенциальная энергия будет равна , где – ускорение силы тяжести, кинетическая энергия маятника равна , где – момент инерции маятника относительно оси вращения;  – угловая скорость – первая производная от угла поворота по времени .

Полная механическая энергия маятника

. (1)

Если угол отклонения от положения равновесия мал, то . Тогда выражение (1) можно переписать в виде

. (2)

Поскольку при колебаниях маятника неизбежно совершается работа по преодолению сил трения, механическая энергия постепенно убывает. Учитывая, что в дальнейшем нас будет интересовать, прежде всего, период колебаний, предположим, что потери энергии за время одного периода по сравнению с полной энергией пренебрежимо малы. Определим уравнение движения, а из него и период колебаний в этом приближении.

Если потерями энергии можно пренебречь, то , а .

Определим производную от энергии по времени из выражения (2) и приравняем ее нулю. В результате получим уравнение

. (3)

Решение дифференциального уравнения (3) имеет вид

, (4)

т.е. маятник совершает гармонические колебания. Здесь  – амплитуда колебаний;  – фаза колебаний;  – круговая (циклическая) частота; – начальная фаза. Амплитуда колебаний и начальная фаза из уравнения (3) не находятся. Они определяются заданием так называемых начальных условий. Круговая частота колебаний определяется видом уравнения (3) и равна корню квадратному из коэффициента перед переменной , т. е.

. (5)

Период колебаний связан с частотой соотношением . Учитывая (5), получим выражение для периода колебаний

. (6)