Раздел 1. Основные понятия и методы математического анализа

Тема 1.1. Функции

Практическая работа №1.

Тема: Исследование функции на непрерывность и вычисление пределов функций.

Цель: Научиться находить точки разрыва функции, вычислять пределы функций в точке и на бесконечности.

Методические указания

Определение 1. Функция f(x) называется непрерывной в точке , если она определена в некоторой окрестности точки х₀ , существует предел функции при и он равен значению функции в этой точке:

Определение 2. Функция f(x) называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.

Определение 3. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Пример 1. Найти точки разрыва функции

Решение. Данная функция определена при всех значениях х, кроме х=1. Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения. Таким образом, точкой разрыва служит точка х=1.

Найдем левый и правый пределы функции при

Следовательно, функция в точке х=1 имеет бесконечный разрыв рода.

Определение 4. Число А называется пределом функции f(x) при х стремящемся к х₀ , если для любого числа существует число , такое, что для всех из условия следует

Определение 5. Число b называется пределом функции y= f(x) на бесконечности, если для всякого числа можно найти такое число , что , когда

Определение 5. Число А называется пределом функции y= f(x), если для всех достаточно больших по модулю значений аргумента х соответствующие значения функции f(x) сколь угодно мало отличаются от числа А.

Теоремы о пределах

Теорема 1. Если существуют пределы функций f(x) и g(x), то существует также и предел их суммы, равный сумме пределов функций f(x) и g(x):

.

Теорема 2. Если существуют пределы функций f(x) и g(x), то существует также и предел их произведения, равный произведению пределов функций f(x) и g(x): .

Теорема 3. Если существуют пределы функций f(x) и g(x) и предел функции f(x) отличен от нуля, то существует также предел отношения f(x)/ g(x), равный отношению пределов функций f(x) и g(x):

.

Следствия. 1. Постоянный множитель можно вынести за знак предела:

2. Если п— натуральное число, то

3. Предел многочлена (целой рациональной функции) при равен значению этого многочлена при х=х₀, т.е

4. Предел дробно-рациональной функции при равен значению этой функции при х=х₀, если х₀ принадлежит области определения функции, т.е.

Правила вычисления пределов

1. При раскрытии неопределенности вида , необходимо разложить числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы о пределе частного двух функций.

2. При после применения теоремы о пределе частного двух функций получаем неопределенность вида . Для ее раскрытия нужно разделить числитель и знаменатель на высшую степень переменной х. Воспользуйтесь наряду с теоремами о пределах и следствиями из них правилом .

3. Для вычисления пределов функций воспользуйтесь замечательными пределами: ,

Пример 2. Найти

Решение. Здесь имеем неопределенность типа . Для того, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель х – 2. В результате получим

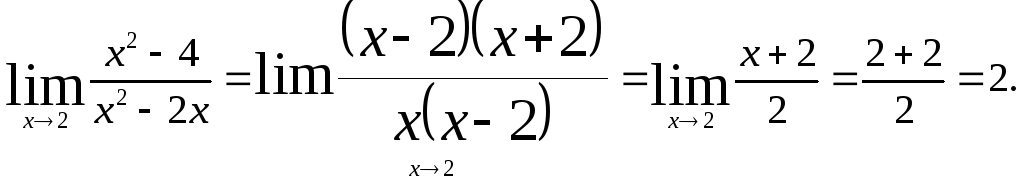
Пример 3. Найти

Решение. Здесь имеем неопределенность типа . Для того, чтобы раскрыть эту неопределенность, разделим числитель и знаменатель дроби на х². В результате получим

Пример 4. Найти

Решение. Произведем подстановку 5х=у. Отсюда следует, что при , а Тогда получим

Пример 5. Найти

Решение. Имеем

Пример 6. Найти

Решение. Имеем