Линейная трендовая модель – 11

V_r= √ (795.7/ 13) / 74.71٭100% = 10.4%

Квадратичная трендовая модель -1v

V_r= √ (88,62 / 13) / 74.71٭100% = 3,4%

Чем меньше процентное отношение, тем точнее модель. Из двух сравниваемых моделей следует отдать предпочтение модели - IV. Поэтому дальнейшие исследования будем проводить с использованием модели – IV, представленной уравнением (47).

4.7. Интерполяция и экстраполяция (прогноз) по трендовой модели

Осуществим интерполяцию выпуска продукции при t=10,5 и экстраполяцию (прогноз) при t=15 с помощью полученной трендовой модели.

Поскольку из двух конкурирующих моделей наиболее достоверной является квадратичная трендовая модель, все расчетные исследования будем проводить именно с этой моделью, поочередно подставляя значения t = 10.5 и t= 15 в модель – 1V или в уравнение (47).

Так как наша модель готовилась со смещением начала координат вправо на 7 лет, а значения даны в абсолютной системе координат, то при вычислении мы будем из значений t вычитать 7. Таким образом:

при t =( 10,5 – 7):

= 82.92+1.43t-0.59t²=82.92+1.43(10.5-7)-0.59(10.5-7)²=87.925-7.2=80.7.

Это значит, что на 10,5 году объем производства составит 80.7 у.е.

При t = (15 – 7)

=82.92+1.43t-0.59t²=82.92+1.43(15-7)-0.59(15-7)²=82.92+11.44-37.76=56.6.

Предполагается, что на 15 году объем производства составит по прогнозу 56.6 у.е.

8. Корреляционные модели

8.1. Корреляционная модель производственного процесса

Пусть 13 одноотраслевых заводов выпускают однотипную продукцию Y_x в некоторых условных единицах. Производительность завода связана с количеством рабочих X_i зависимостью

Y_x = f(X_i).

Определить уравнение связи между объемом выпускаемой продукции Y_x и количеством рабочих на заводе X_i. В качестве исходной примем исходную расчетную таблицу 2 для трендовых моделей, осуществив замену:

Y_x = Y_t ; X_i = 100t_i

x_i = 100^-1٭X_i .

8.2. Линейная корреляционная модель

Поскольку мы используем весь заданный интервал для х (от 1 до 13), при написании пределов суммы не будем указывать параметры интервала.

Запишем функционал:

S=∑( Y_х–)²→min. (49)

В качестве выравнивающей примем линейную функцию

=A+Bх. (50)

Тогда (49) с учетом (50) примет вид

S=∑( Y_х – A - Bх)²→min. (51)

Частные производные по искомым параметрам А и В запишутся в виде системы:

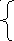
= 2 ∑( Y_х – A – Bх)*(-1) = 0, (52)

= 2 ∑( Y_х – A – Bх)*(-х) = 0. (53)

Откуда можно записать систему нормальных уравнений

N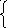А + В∑ х = ∑Y_х , (54)

А∑ х+ В∑ х ² = ∑Y_х х. (55)

Подставим известные из таблицы 4 значения ∑ х , ∑Y_х , ∑ х ² и ∑Y_х х в уравнения (54) и (55), получим:

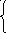13A + 91B = 971.3, (56)

91A + 819B = 7059,8. (57)

Решение этой системы дает:

A=64.71; B=1.43. (58)

Таким образом, линейная корреляционная модель представляет собой уравнение:

=64.71+1.43х. ( V) (59)