2. Выполнение задания по курсовой работе

1. Таблица исходных данных производительности завода по годам в течение 13 лет.

Пусть задание дается для группы 9ЭФМе-2.Фамилия студента в списке группы включена под нечетным номером 5. Тогда в соответствии с заданием коэффициенты исходной модели примут значения:

v = 5; Г = 2; N=13;

а₀ = 10٭v = 50;

a₁ = v + 0,2٭Г = 5 + 0,2٭2 = 5.4;

a₂=0,5٭v = 0,5٭5 = 2,5;

f(t)= cos 1,57t.

Модель производительности завода (уравнения (0.1) и (0.2)) с учетом значений подсчитанных коэффициентов примет вид:

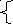50 + 5.4t + 2.5cos1,57t, 0 < t ≤ 7;

Y_t= Y_t=7 – 0,5٭5.4٭(t - 7) + 2.5 cos 1,57t, 7 < t ≤ 13.

Значения cos 1,57t при изменении аргумента t от 0 до 13 определяются из таблицы (0.1).

Расчет значений производительности предприятия по годам определяется по вышеприведенным формулам:

Y_t=1= 50+5.4*1+2.5cos1.57*1=50+5.4+2.5*0=55.4;

Y_t=2=50+5.4*2+2.5cos1.57*2=50+10.8-2.5=58.3;

Y_t=3=50+5.4*3+2.5cos1.57*3=50+16.2+0=66.2;

Y_t=4=50+5.4*4+2.5cos1.57*4=50+21.6+2.5=74.1;

Y_t=5=50+5.4*5+2.5cos1.57*5=50+27+0=77;

Y_t=6=50+5.4*6+2.5cos1.57*6=50+32.4-2.5=79.9;

Y_t=7=50+5.4*7+2.5cos1.57*7=50+37.8+0=87.8; Y_{t = 7} =87.8;

Y_t=8=87.8-0.5*5.4(8-7)+2.5cos1.57*8=87.6;

Y_t=9=87.8-0.5*5.4(9-7)+2.5cos1.57*9=82.4;

Y_t=10=87.8-0.5*5.4(10-7)+2.5cos1.57*10=77.2;

Y_t=11=87.8-0.5*5.4(11-7)+2.5cos1.57*11=77;

Y_t=12=87.8-0.5*5.4(12-7)+2.5cos1.57*12=76.8;

Y_t=13=87.8-0.5*5.4(13-7)+2.5cos1.57*13=71.

Полученные значения включаем в таблицу 1 при этом дополнительно включаем в нее во второй столбец t² и в четвертый столбец произведение Y_tt, необходимые для дальнейших расчетов.

Таблица исходных данных Таблица 1

1	2	3	4
t	t2	Yt	Ytt
1	1	55.4	55.4
2	4	58.3	116.6
3	9	66.2	198.6
4	16	74.1	296.4
5	25	77	385
6	36	79.9	479.4
7	49	87.8	614.6
8	64	87.6	700.8
9	81	82.4	741.6
10	100	77.2	772
11	121	77	847
12	144	76.8	921.6
13	169	71.6	930.8
∑ t=91	∑ t2 =819	∑Yt =971,3	∑Ytt = 7059,8

3. Определение простой средней арифметической _ар:

_ар = ∑Y_t/ N; (1)

_ар = 971,3/13=74,71;

_ар = 74,71.