2. Функции

Функция

– прямая пропорциональная зависимость.

График функции

– прямая (линия).

График проходит через начало координат – точку .

– угловой коэффициент прямой.

Область определения – вся числовая ось: .

Область значений – вся числовая ось: .

Функция нечётная, так как .

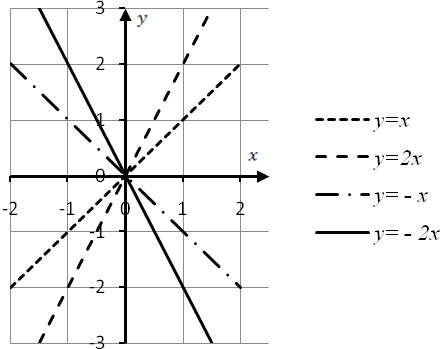
Пример 1. В системе координат начертим графики функций Для построения прямой линии необходимо две точки. Зададим таблицы значений.

Функция возрастает, т.к.

Функция убывает, т.к. .

Рисунок 11.9

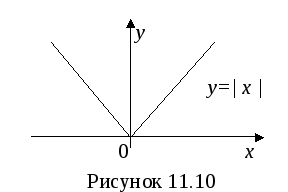
Функция

для любого x

Функция чётная, т.к. .

область определения, область значений.

График функции симметричен относительно оси

Построение графиков методом преобразований

Функция , , – график функции .

смещение на a вправо.

смещение на a влево.

смещение на b вверх.

смещение на b вниз.

смещение на a вправо и на b вверх

Пример 2. Построим графики функций и .

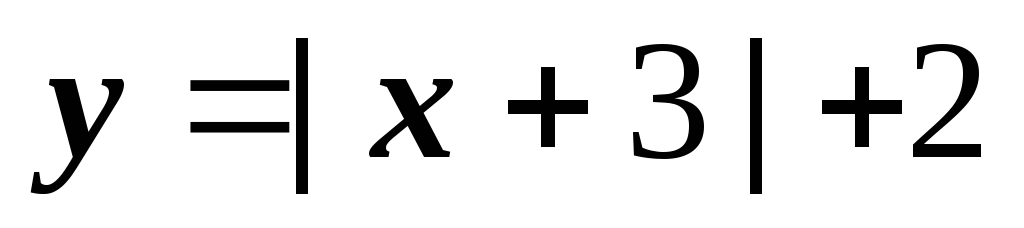1. . Смещение графика функции 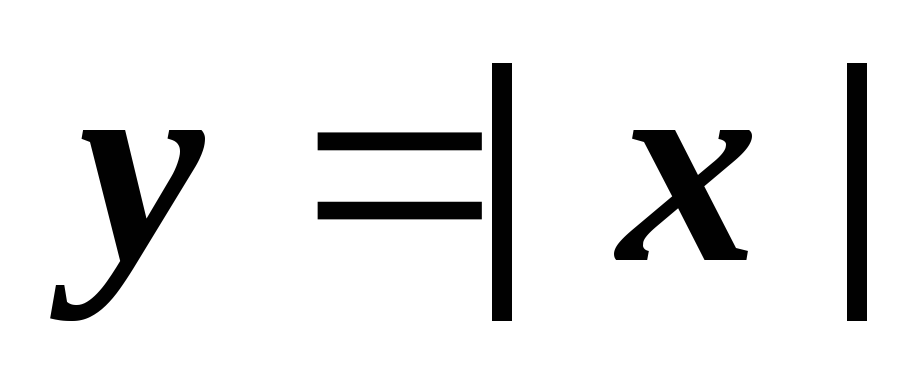на 3 влево и на 2 вверх. Функция 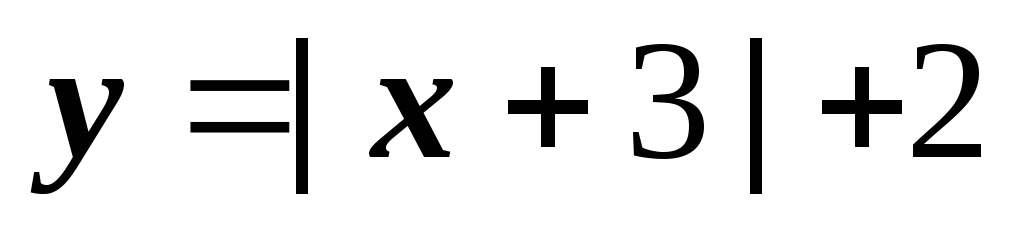убывает при 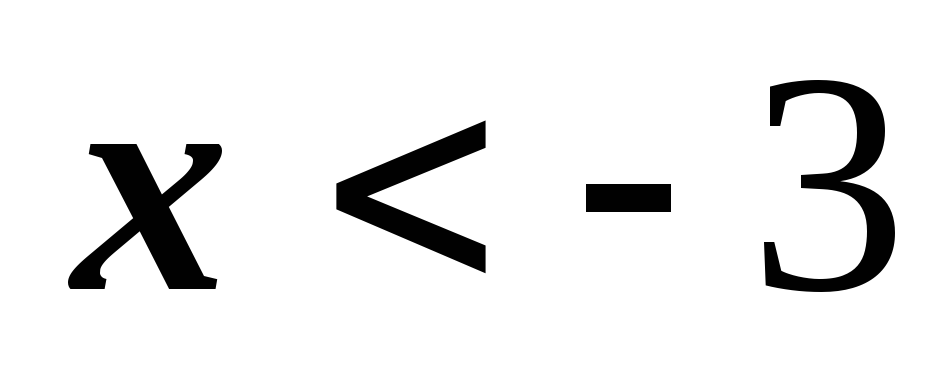и возрастает при .

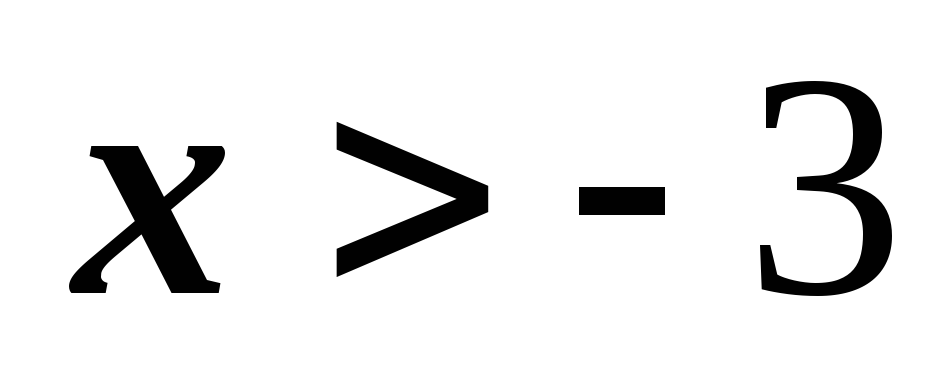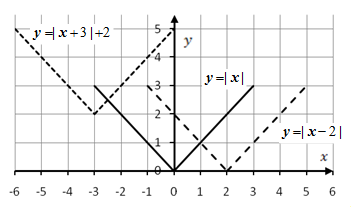
Рисунок 11.11

6. Постройте график функции:

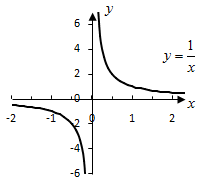
Функция задаёт обратную пропорциональную зависимость.

область определения.

точка разрыва функции.

область значений.

График функции называется гипербола.

Рисунок 11.12

Пример 3. Построим график функции по точкам. Зададим таблицу значений:

Функция убывает. Функция нечётная.

График функции симметричен относительно начала координат – точки .

Задания для решения

1. На одной координатной плоскости методом преобразований постройте графики функций , , .

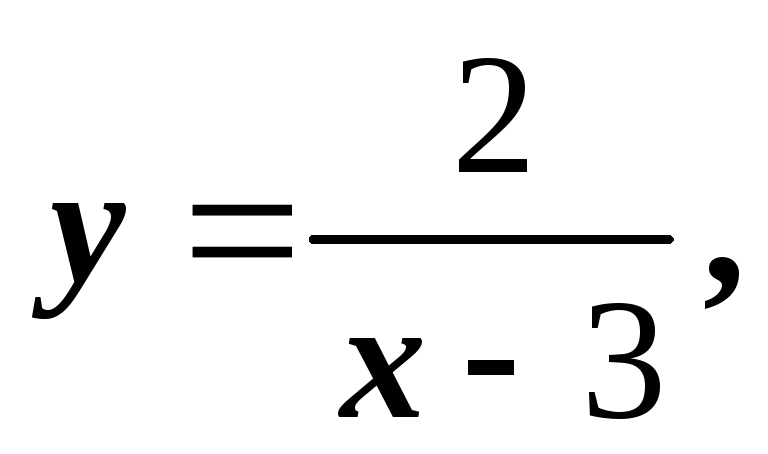
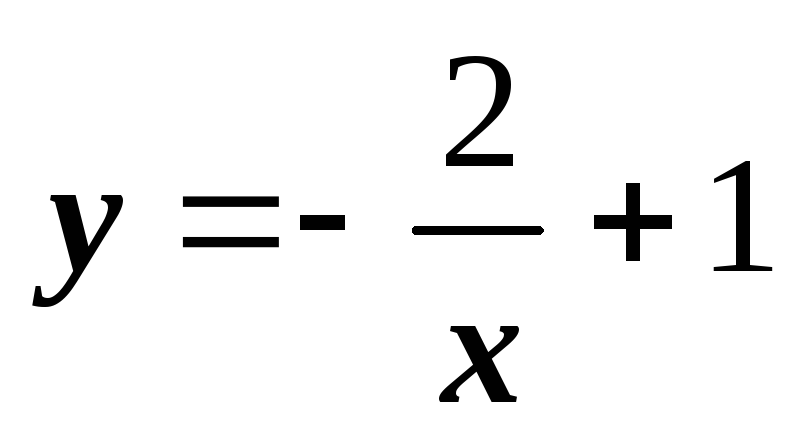3. Линейная функция

линейная функция.

График линейной функции – прямая (линия). обозначение прямой.

Прямая пересекает ось в точке b. k – угловой коэффициент прямой.

две прямые.

1. Прямые параллельны, если .

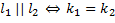
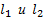
2. Прямые пересекаются, если .

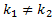прямые и пересекаются в точке A.

3. Прямые 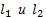перпендикулярны, если .

Пример 1. В системе координат построим прямые и .

– точка пересечения прямых.

Прямые перпендикулярны, т.к. , , .

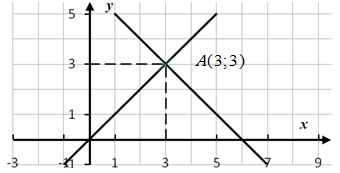
Рисунок 12.2