3. Окружность и круг

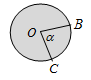
	Окружность О – центр окружности OA = R – радиус окружности АВ – диаметр окружности, АВ = 2R AD – хорда , BD – дуга C=2R длина окружности
 – центральный угол. Дуга BD стягивает угол  длина дуги BCD – вписанный угол. BCD опирается на дугу BD
	AB – касательная AD – секущая BE – хорда
	Круг. площадь круга BOC – круговой сектор – площадь сектора

Задания для решения

1. Длина окружности равна 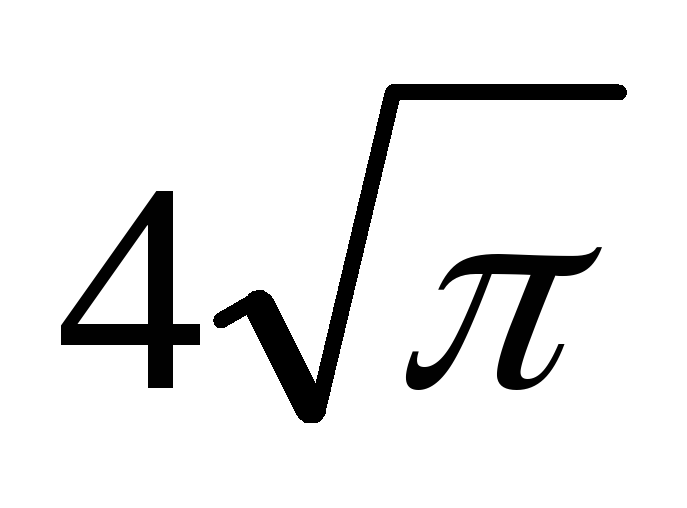. Найдите площадь круга.

2. Радиусы кругов относятся как 1:2. Длина окружности большего круга равна 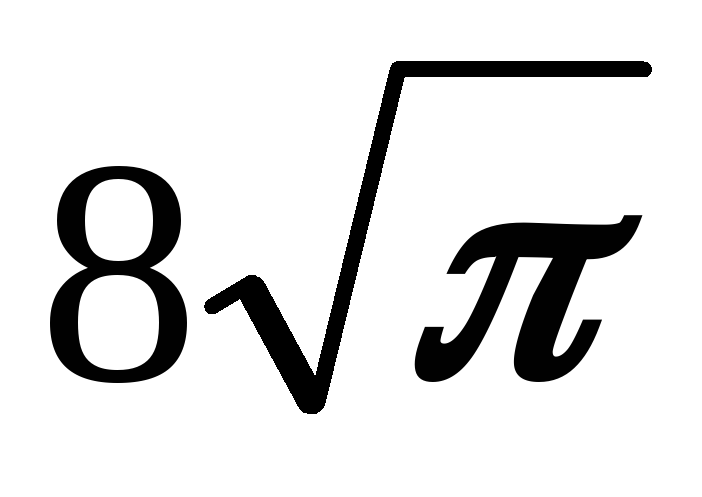. Найдите площадь меньшего круга.

3. Площади кругов относятся как 1:16. Радиус меньшего круга равен 4/. Найдите длину окружности большего круга.

4. Во сколько раз увеличится длина окружности, если её радиус увеличить в 3 раза?

5. Во сколько раз увеличится площадь круга, если его радиус увеличить в 2 раза?

6. Во сколько раз увеличится длина окружности, если площадь её круга увеличить в 16 раз?

7. Площадь кругового сектора с центральным углом 20^о равна 2. Найдите радиус сектора.

8. Дана окружность радиуса 26 см. Длина хорды равна 48см. Найдите расстояние от центра окружности до хорды.

Ответы:

1. 4. 2. 4. 3. 32. 4. 3. 5. 4. 6. 4. 7. 6. 8. 10см.

4. Функции

1. Основные понятия

–функция

– независимая переменная, – зависимая переменная. Независимую переменную называют аргументом. Зависимая переменная – это функция аргумента .

Значения независимой переменной образуют область определения функции (дэ от игрек). Значения зависимой переменной образуют область значений функции .

Функция .

Область определения , область значений E

Способы задания функции

Задать функцию значит указать, как по каждому значению находить значение функции .

Рассмотрим три основных способа задания функции: аналитический, табличный, графический.

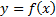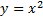1. Аналитический способ, т.е. с помощью формулы . Формула задаёт функцию с областью определения 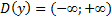и такой же областью значений. Формула 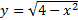задаёт функцию с областью определения 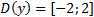и областью значений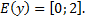

2. Табличный способ. Значения аргумента 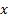и соответствующие значения функции показаны в таблице:

   x	0
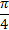
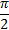
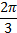
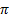
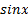
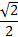
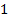
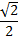
   	0								0

3. Графический способ. Функция задаётся графиком.

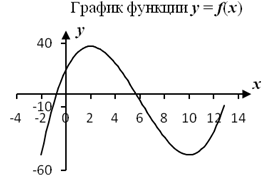
Свойства функций

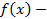1. чётная функция, если ,

нечётная функция, если ,

График чётной функции симметричен относительно оси (рисунок 11.4). График нечётной функции симметричен относительно начала координат – точки (рисунок 11.5).

Рисунок 11.4

Рисунок 11.5

2. 

возрастает, если

убывает, если