Задания для решения

3. Решите уравнение с помощью замены переменной:

4. Множества

   1. Числовые множества

множество натуральных чисел

множество целых чисел

множество рациональных чисел.

множество иррациональных чисел.

множество действительных чисел.

, - отношения включения между множествами.

2. Операции над множествами

Рассмотрим множества:

множество B равно множеству C , т.к. B и C состоят из одинаковых элементов.

D подмножество A, т.к. элементы множества D принадлежат множеству A.

_ пустое множество.

Пустое множество _ не содержит элементов.

1. П ересечение множеств

пересечение множеств A и B равно Х.

знак пересечения

Множество Х содержит одинаковые элементы A и В.

пересечение множеств пусто, т.к. A и M не содержат одинаковых элементов.

2. Объединение множеств

объединение множеств A и B равно Y.

знак объединения

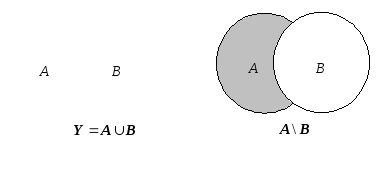
2. Разность множеств

разность множеств и .

Из множества A убираем одинаковые элементы A и B.

разность множеств

Из множества B тоже убрали элементы 2 и 4.

отрезок ab

интервал ab

полуинтервал ab

полуинтервал ab

Пример 1. Даны множества .

, , , .

Задания для решения

1. Даны множества A и B. Найдите пересечение, объединение и разность множеств А и В.

.

4. Прямоугольная система координат

   1. Прямоугольные координаты точки

Две взаимно перпендикулярные оси и , имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат (рисунок 3.1).

Ось называется осью абсцисс, ось – осью ординат. Обе оси называются осями координат. Плоскость, в которой расположены оси и , называется координатной плоскостью и обозначается .

Пусть М – произвольная точка плоскости. Опустим из нее перпендикуляры МА и МВ на оси и соответственно.

Прямоугольными координатами и точки М будем называть соответственно величины ОА и ОВ направленных отрезков и : , (рисунок 3.1). Координаты и точки M называются соответственно её абсциссой и ординатой. Запись обозначает точку М с координатами , , причём первой всегда указывают абсциссу, а второй – ординату. Точка О имеет координаты (0;0).

Таким образом, при выбранной системе координат каждой точке М плоскости соответствует единственная пара чисел – ее прямоугольные координаты. И, обратно, любой паре чисел соответствует единственная точка М плоскости такая, что ее абсцисса равна , а ордината равна . Это означает, что между точками плоскости и множеством пар чисел существует взаимно однозначное соответствие, что даёт возможность при решении геометрических задач применять алгебраические методы.

Оси координат разбивают плоскость на четыре координатных угла (рисунок 3.2). На рисунке 3.2 показаны знаки координат точек в зависимости от их расположения.

2. Векторы на плоскости и в пространстве

Вектором называется направленный отрезок с началом в точке и концом в точке . Вектор можно перемещать параллельно самому себе. Векторы можно обозначать двумя прописными буквами или одной строчной буквой (рисунок 3.3).

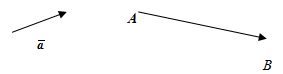
Рисунок 3.3

Длиной (или модулем) вектора называется число, равное длине отрезка .

Если начало и конец вектора совпадают, то такой вектор называется нулевым.

Координаты вектора. Перенесём вектор параллельно самому себе так, чтобы его начало совпало с началом координат.

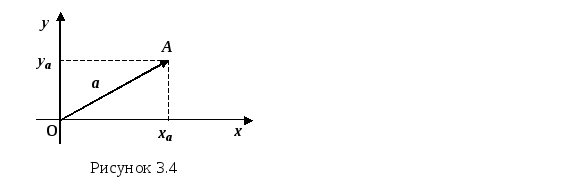
Координатами вектора называются координаты его конца: (рисунок 3.4).

Если , – две произвольные точки плоскости, то координаты вектора находим вычитанием из координат конца координат его начала:

.

- мерным вектором называется упорядоченная совокупность n действительных чисел (), записываемых в виде , где – i-тая координата вектора. Множество n-мерных векторов называют векторным пространством и обозначают . Мы будем рассматривать только векторы на плоскости (пространство ) и в трёхмерном пространстве . Рассмотрим два вектора и из пространства .

Суммой (разностью) двух векторов и называется вектор, координаты которого равны сумме (разности) соответствующих координат векторов и :

,

.

Складывать и вычитать можно только векторы одинаковой размерности. Например, если даны векторы , , , , то можно сложить векторы и или и :

; .

Произведением вектора на число называется новый вектор , координаты которого равны координатам вектора , умноженным на число :

.

Векторы и называются коллинеарными, если их соответствующие координаты пропорциональны:

.

Коллинеарные векторы лежат на одной прямой или на параллельных прямых.

Пример 3.1. При каких значениях х, у векторы и коллинеарны?

Решение. Координаты векторов в этом случае пропорциональны, т.е.

. Тогда

Таким образом, получаем векторы , которые коллинеарны.