10. Приложения последовательностей в финансовой математике

Последовательности. Числовой последовательностью называют функцию , заданную на множестве натуральных чисел. Арифметическая и геометрическая прогрессии – примеры последовательностей, которые изучают в школьном курсе математики. Последовательность обозначают или .

Последовательность называется ограниченной сверху (снизу), если существует число () такое, что () для всех . Ограниченная сверху и снизу последовательность называется просто ограниченной.

Последовательность ограничена сверху, Все её элементы меньше числа 2. Последовательность ограниченная: все её элементы больше 0, но не больше 5.

Последовательность называется возрастающей (неубывающей), если (); убывающей (невозрастающей), если (); монотонной, если она или неубывающая, или невозрастающая.

Например, последовательности , ограничены, при этом первая убывает, а вторая возрастает.

Примером последовательностей являются наращенные денежные суммы, положенные в банк. Когда в банк делают вклад, то банк получает возможность распоряжаться (в определённых пределах) вложенной суммой. Выплата процентной ставки есть плата банка за возможность распоряжаться деньгами вкладчика в течение срока договора.

Пример 5. В банк сделан вклад руб. при процентной ставке p%. Сумма , которая будет получена через время при условии начисления простых процентов, выражается формулой . Следовательно, зависимость наращенной суммы от времени выражается линейной функцией. Однако иногда начисление производится только по прошествии целого числа лет. В этом случае наращенная сумма является арифметической прогрессией с начальным (нулевым) членом и разностью .

Пример 6. Пусть начисляются сложные проценты. Тогда наращенная сумма , которая будет получена через время , выражается формулой . Следовательно, зависимость наращенной суммы от времени выражается показательной функцией. Если начисление производится только по прошествии целого числа лет, то наращенная сумма является геометрической прогрессией с начальным (нулевым) членом и показателем .

В обоих случаях называется начальной суммой, а – наращенной суммой. Разница называется процентным платежом или начисленными процентами. В случае простых процентов .

С другой стороны, пусть имеется вексель на 1000 ден.ед., выданный 2 декабря под 20% годовых с погашением через год. Но векселедержателю к началу сентября очень понадобились деньги, и он 31 августа понёс вексель в банк. Принятие векселя и выплата денег векселедержателю называется учётом векселя в банке. Теоретически банк должен был выплатить сумму из расчёта (степень ¼ взята потому, что до погашения векселя осталось 3 месяца=1/4 года), т.е. ден.ед. Поскольку банки берут плату за совершение денежных операций, то выплачено будет 950 ден.ед.

Вообще задача определения эквивалента в момент времени денежной суммы, которая в момент времени была равна , называется дисконтированием, т.е. приведением к другому моменту. Если процентная ставка неизменна и начисляются сложные проценты, то .

Все эти рассуждения не учитывают инфляции. Говорят, что инфляция составляет % в год, если один и тот же набор товаров через год окажется стоящим на % больше. Иначе говоря, реальное содержание денежной суммы уменьшается через год в раз, а через лет в раз. В нормальной экономике процентная ставка больше, чем темп инфляции.

Пусть норма процента – % в год, а инфляция – % в год. Тогда через год сумма возрастёт на % из-за наращения по норме процента, но эта же сумма будет обладать в раз меньшей покупательной способностью, следовательно, её реальное денежное содержание будет равно . Отсюда следует простой вывод – реальное содержание денежной суммы:

Найдём рыночную стоимость бессрочной облигации. Гашение такой облигации не предусмотрено, но каждый год владелец получает так называемый купонный доход. Если облигация номинала 1000 ден.ед. имеет 3%-купон, значит, каждый год она приносит владельцу доход 30 ден.ед. Предположим, что тем инфляции 2%. Рыночная цена облигации будет равна дисконтированию ряда будущих ежегодных платежей в 30 ден.ед. по ставке 2%, т.е. сумме геометрической прогрессии с первым членом 30 и знаменателем (облигация продаётся сразу же после получения очередного купонного дохода). Напомним, что сумма членов бесконечной геометрической прогрессии находится по формуле . Получаем окончательно:

.

Это и есть рыночная цена облигации.

Задачи

1. руб. вложены в банк под 6% годовых на полгода (проценты простые). Найти наращенную сумму. (Ответ: 26000 руб.)

2. Банк ежегодно выплачивает 5% годовых (сложный процент). Определить размер вклада через 3 года, если первоначальный вклад был 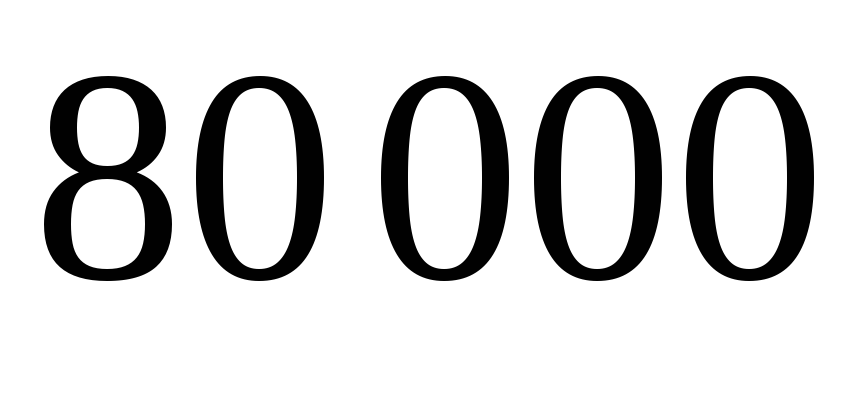тыс. руб. (Ответ: 92610 руб.)

3. Банк выплачивает ежегодно 5% годовых (сложный процент). Определить размер первоначального вклада, при котором через 4 года вклад (вместе с процентными деньгами) составит 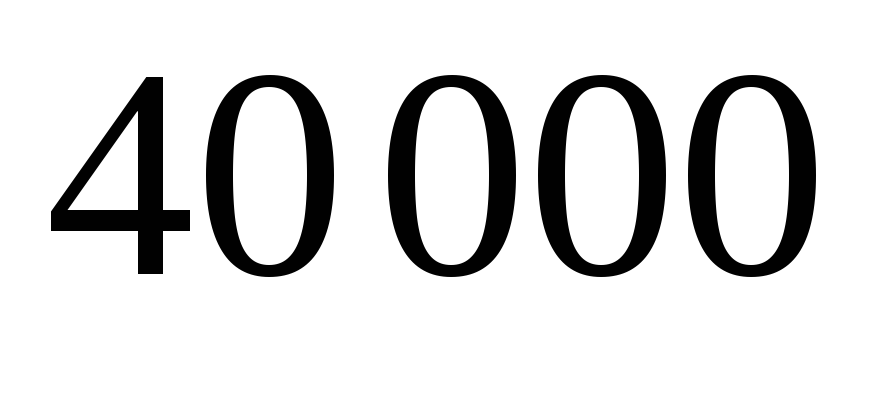тыс. руб. (Ответ: 32908 руб.)

4. Банк выдал кредит руб. В договоре принята ставка простых процентов за первые 0,5 года, равная 20 % годовых, а каждые последующие 0,5 года ставка увеличивается на 3 % по сравнению с предыдущей. Срок договора равен 2 годам. Определить наращенную сумму за весь срок договора. (Ответ: 1490000 руб.)

5. Между двумя капиталами разница в 300 $. Капитал большего размера вложен на 6 месяцев при ставке простых процентов 5% годовых, а капитал меньшего размера – на 3 месяца при ставке 6%. Начисленные проценты на первый капитал в два раза больше процентов, начисленных на второй капитал. Найти величину капиталов. (Ответ: 1500$ и 1800$.)

6. На сколько лет должна быть вложена сумма 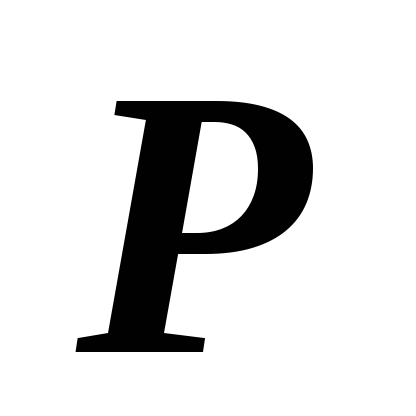при ставке простых процентов 6% годовых, чтобы процентный платёж в три раза превысил 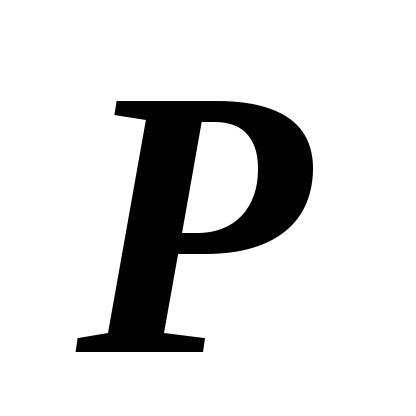? (Ответ: 50 лет.)

7. Через 90 дней после подписания договора на 100000 руб. должник уплатит 105000 руб. Определить процентную ставку (проценты обыкновенные: год – 360 дней, каждый месяц – 30 дней). (Ответ: 20 %.)

8. Через 8 лет по обязательству будет выплачено 10 млн руб. Определить современную стоимость обязательства при условии, что применяется ставка сложных процентов 10 % годовых. (Ответ: 4665073,8 руб.)