3. Тригонометрические преобразования и уравнения

Тригонометрические формулы

1) ;	6) ;
2) ;	7) ;
3) ;	8) ;
4) ;	9) ;
5) ;	10) ;
11) ;
12) ;
13) ;
14) ;
15) ;		16) .

Пример 3. Преобразуем выражение и вычислим его значение, если .

Решение. По формулам 4) и 6)

, .

По формуле 5) .

По формулам 1) и 16) .

Задания для решения

4. Преобразуйте выражение и вычислите его значение:

   а) 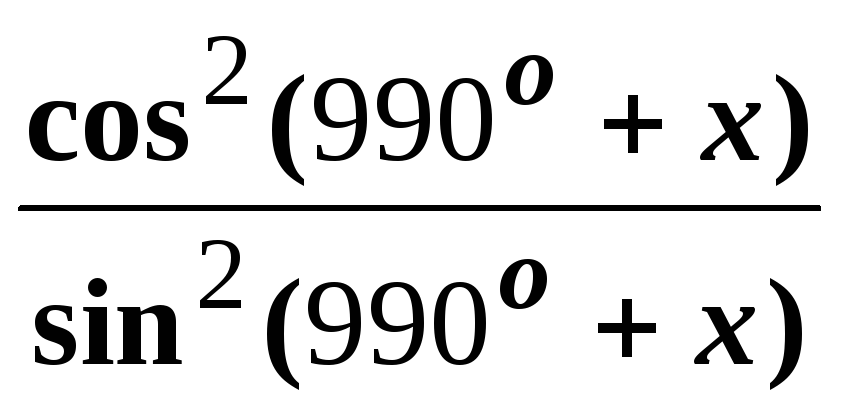,если ;

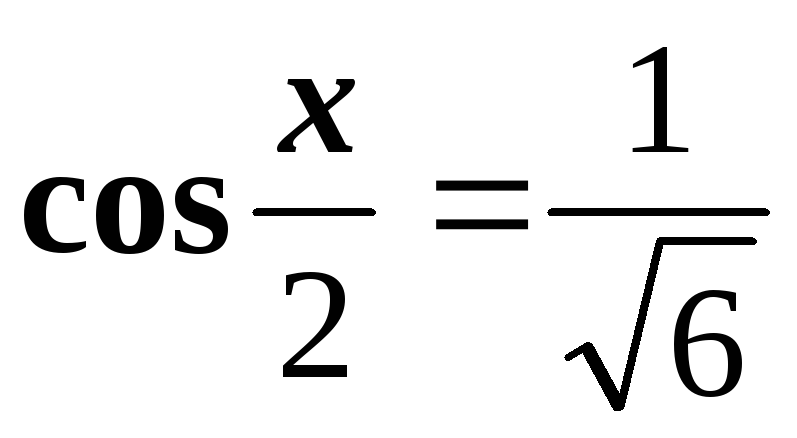   б) 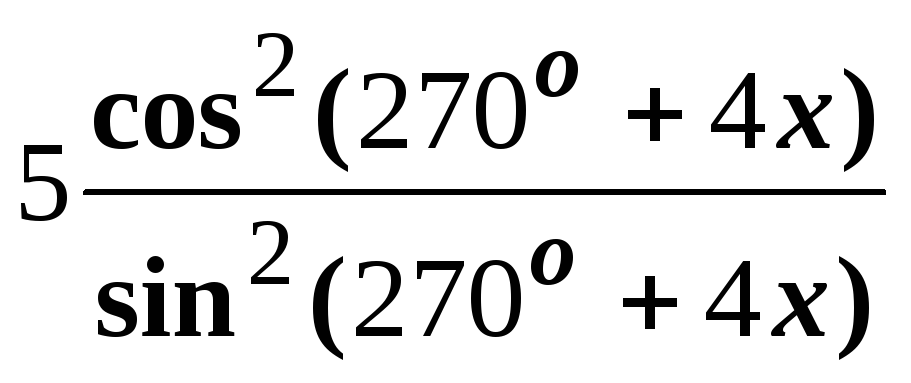, если ;

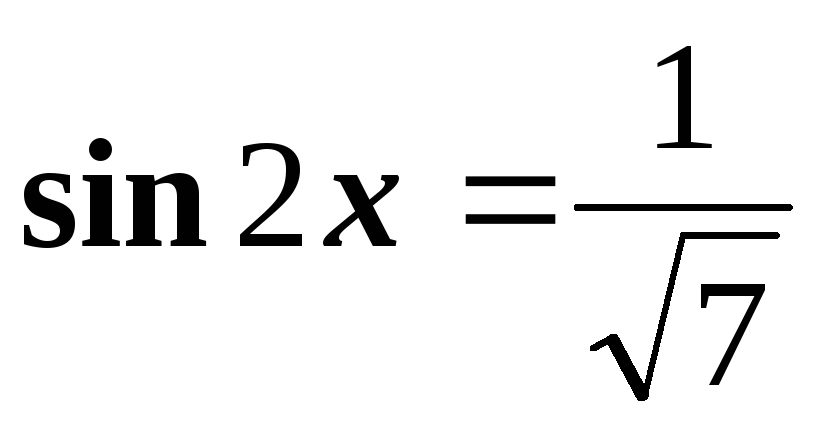   в) , если ;

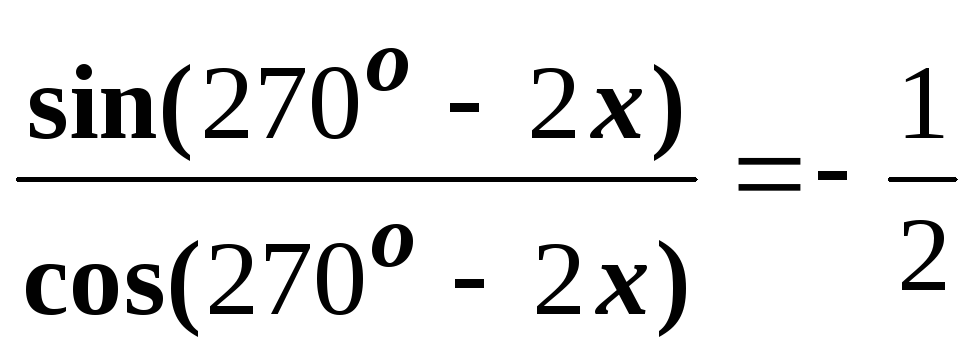   г) 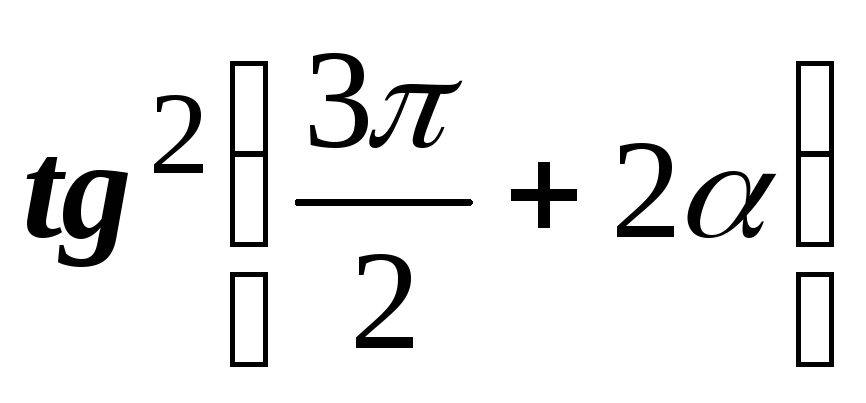, если ;

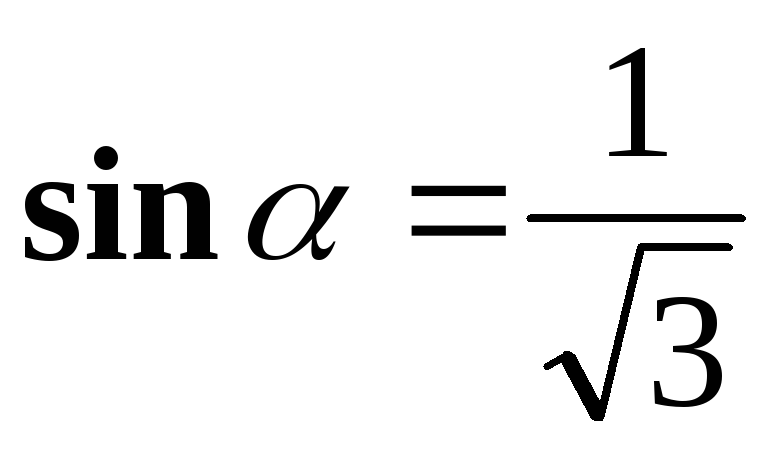   д) 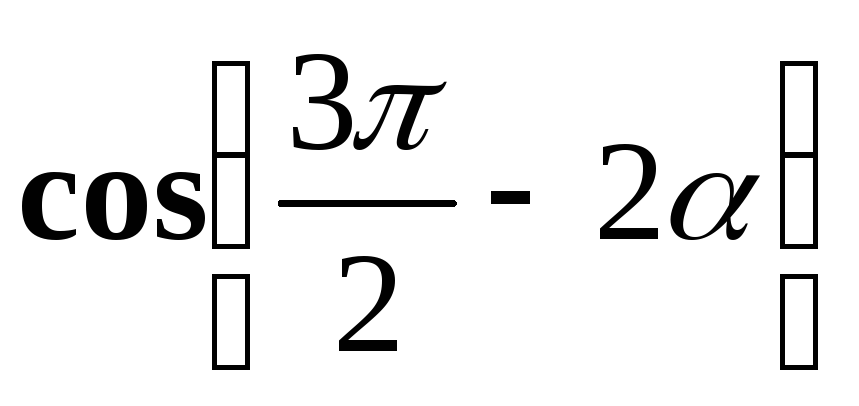, если .

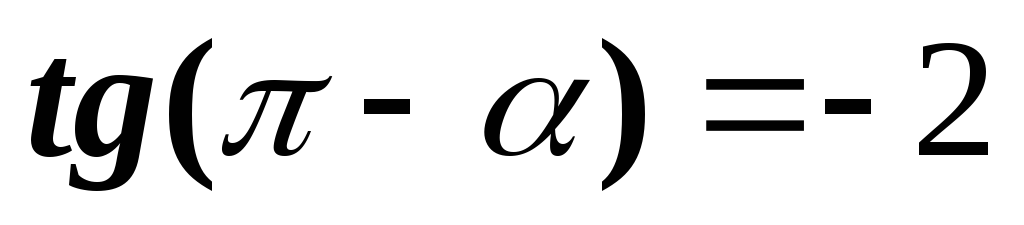5. Упростите выражение:

   а) 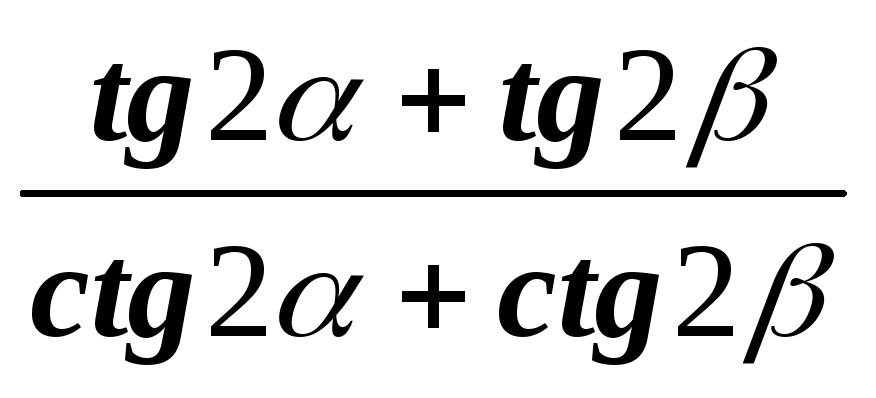;	б) ;
   в) 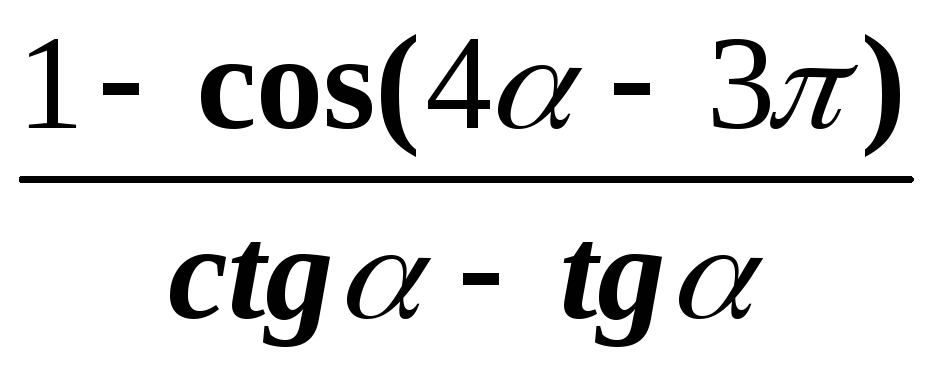;	г) ;
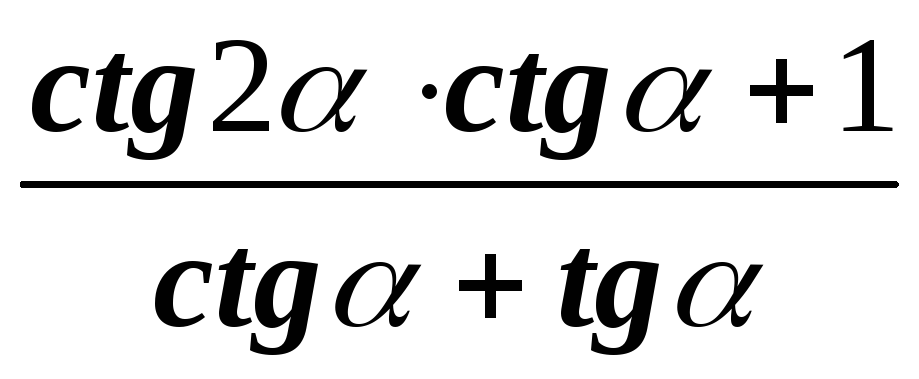   д) ;
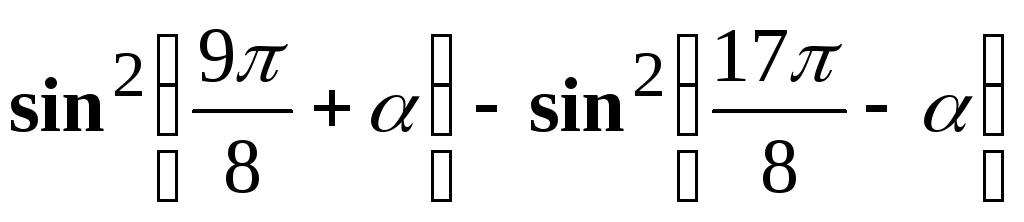   е) ;
   ж) .

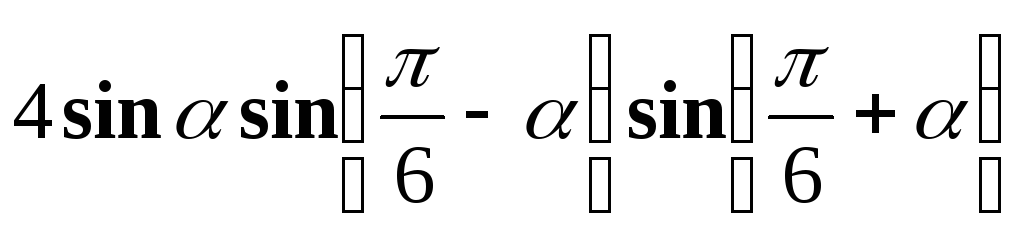6. Решите уравнения:

   1) 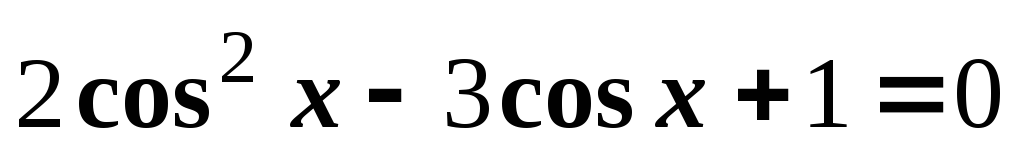. Отв. .

   2) 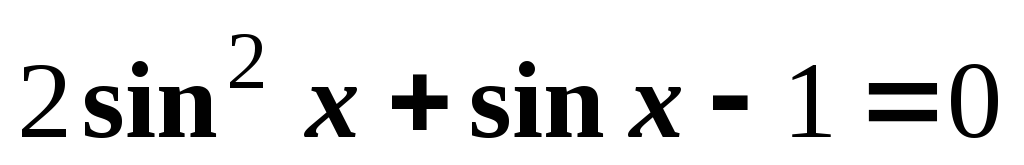. Отв. .

   3) 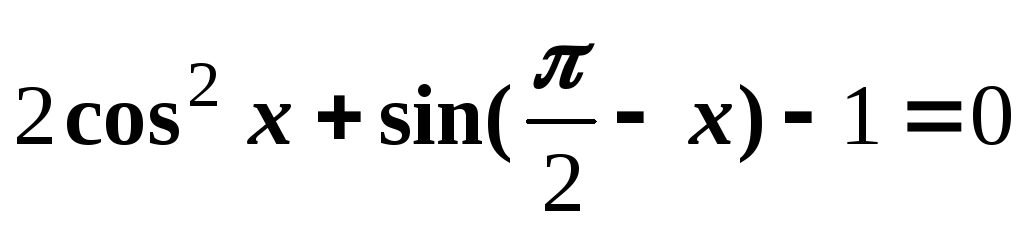. Отв. .

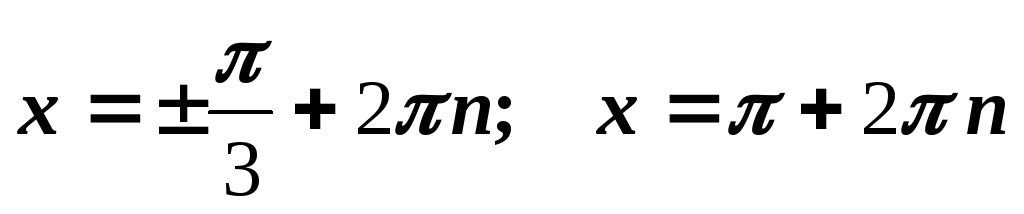   4) . Отв. .

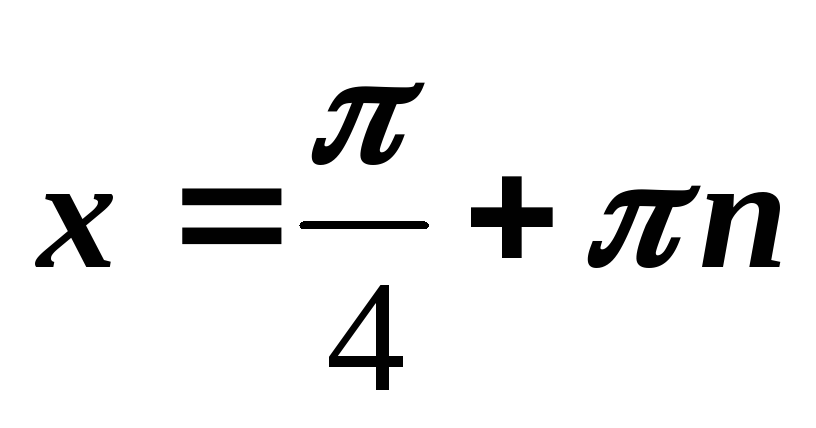7. Найдите значение выражения

1) ;	3) ;	5) ;
2) ;	4) ;	6) .

10. Арифметическая и геометрическая прогрессии

1. Арифметическая прогрессия

– арифметическая прогрессия.

, – формулы n-го члена арифметической прогрессии.

D – разность арифметической прогрессии.

– сумма n первых членов арифметической прогрессии.

– формула для вычисления суммы n первых членов арифметической прогрессии.

– формула для вычисления суммы n первых членов арифметической прогрессии.

арифметическая прогрессия.

первый член арифметической прогрессии,

второй член арифметической прогрессии,

десятый член арифметической прогрессии,

эн плюс первый член арифметической прогрессии.

сумма десяти первых членов арифметической прогрессии.

?

Пример 1. Найти арифметическую прогрессию, если её четвёртый член равен 11, а седьмой член равен 20.

Решение. .

. Разность арифметической прогрессии . Найдём первый член: , .◄

Задачи.

1. Найти арифметическую прогрессию, если сумма второго и пятого членов равна 14, а сумма третьего и восьмого членов равна 6.

2. Найти арифметическую прогрессию, если сумма первых трёх её членов равна нулю, а сумма их квадратов равна 8.

3. Найти арифметическую прогрессию, в которой сумма первых трёх её членов равна 15, а произведение этих же членов равно 80.

4. В арифметической прогрессии найти:

9. Геометрическая прогрессия

– геометрическая прогрессия

– формула n-го члена геометрической прогрессии.

– первый член геометрической прогрессии,

– n-ый (энный) член геометрической прогрессии,

q – знаменатель геометрической прогрессии,

– сумма n первых членов геометрической прогрессии,

– формула для вычисления суммы n первых членов геометрической прогрессии.

Если – сумма членов бесконечно убывающей геометрической прогрессии.

Пример 2. геометрическая прогрессия: первый член геометрической прогрессии, знаменатель геометрической прогрессии, второй член геометрической прогрессии, третий член геометрической прогрессии,

, , .

Сумма первых шести членов геометрической прогрессии:

.

Пример 3. бесконечно убывающая геометрическая прогрессия,

первый член геометрической прогрессии, знаменатель геометрической прогрессии, второй член геометрической прогрессии, третий член геометрической прогрессии, , .

сумма членов бесконечной убывающей геометрической прогрессии.

Пример 4. Сумма первого и третьего членов геометрическая прогрессии равна 20, а сумма второго и четвёртого членов равна 60. Найти геометрическую прогрессию.

Решение. Сумма первого и третьего членов геометрическая прогрессии равна 20: . Сумма второго и четвёртого членов равна 60: .

Тогда , .

, .

– геометрическая прогрессия.◄

Задачи.

4. Разность между шестым и четвёртым членами геометрической прогрессии равна 216, а разность между третьим и первым членами равна 8. Найти сумму первых восьми членов этой прогрессии.

5. Найти сумму бесконечно убывающей геометрической прогрессии, второй член которой равен 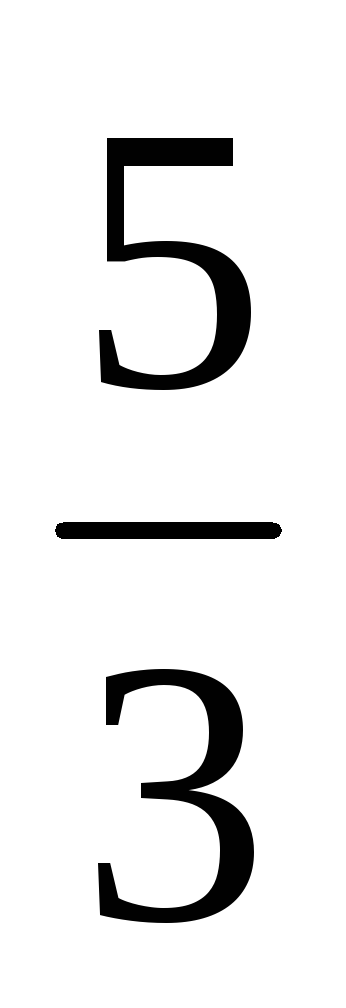, а знаменатель равен .

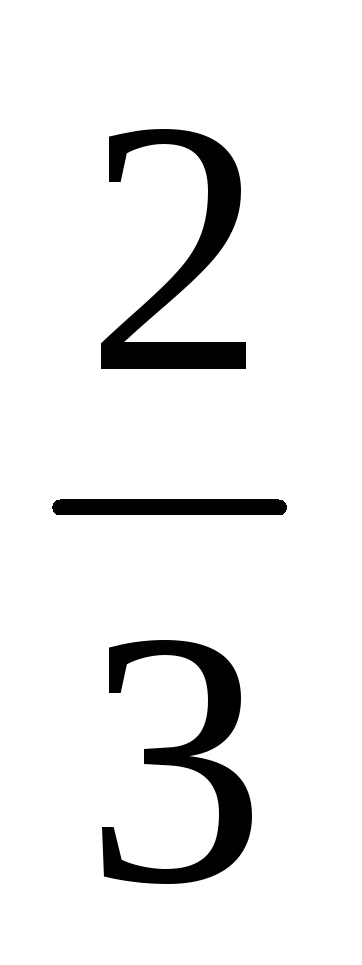6. Найти сумму бесконечно убывающей геометрической прогрессии, если сумма её первого и четвёртого членов равна 54, а сумма второго и третьего равна 36.

7. В геометрической прогрессии 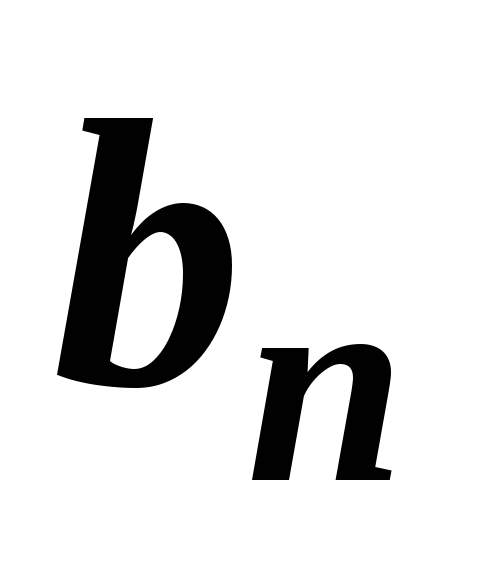найдите