14. Основні властивості перетворення Фур’є (16)

Свойства преобразования Фурье

Под свойствами преобразования Фурье подразумевается взаимное соответствие трансформаций сигналов и их спектров. Хорошее знание свойств преобразова­ния Фурье позволяет предсказывать примерный (а иногда и точный) вид спектра анализируемого сигнала и таким образом контролировать правдоподобность результата, выдаваемого компьютером.

Линейность

Преобразование Фурье является линейным интегральным преобразованием. Смысл свойства линейности можно сформулировать так: спектр суммы равен сумме спектров. Говоря математическим языком, линейная комбинация сигналов име­ет спектр в виде такой же (с теми же коэффициентами) линейной комбинации их спектральных функций:

Если

Задержка

А теперь посмотрим, как сказывается на спектральной функции задержка сигна­ла во времени. Итак, пусть т (тао)-— время задержки:

тогда спектральная функция изменится следующим образом:

Результат показывает, что спектр исходного сигнала оказался умноженным на комплексную экспоненту вида . Таким образом, амплитудный спектр сигна­ла не меняется (ведь модуль такой комплексной экспоненты равен 1; к тому же здравый смысл подсказывает, что соотношение между амплитудами спектраль­ных составляющих из-за сдвига сигнала во времени измениться не должно). Фа­зовый спектр приобретает дополнительное слагаемое , линейно зависящее от частоты

Изменение масштаба оси времени

Рассматривая конкретные примеры, мы уже познали на практике общее прави­ло: чем короче сигнал, тем шире его спектр. Теперь взглянем на это правило со строгих теоретических позиций. Если изменить длительность сигнала f(t) со­храняя его форму, то новый сигнал s(t) следует записать как

.

При \а\>1 сигнал сжимается, при \а\<1 — растягивается. Если а <0, дополни­тельно происходит зеркальное отражение сигнала относительно вертикальной оси. Посмотрим, как такое преобразование сказывается на спектре:

Итак, изменение длительности сигнала приводит к изменению ширины спектра в противоположную сторону (аргумент t на а умножается, а со делится) в сочета­нии с увеличением (при растяжении, а<1) или уменьшением (при сжатии, а > 1) уровня спектральных составляющих. Полученная формула справедлива для а>0. При а<0 использованная замена переменной t->аt вызовет перестановку пределов интегрирования и, как следст­вие, изменение знака у результата:

Объединяя оба случая, можно записать

В частном случае а= -1 полученная формула дает следующее:

Итак, зеркальное отражение сигнала относительно начала отсчета времени при­водит к зеркальному отражению спектра относительно нулевой частоты. Для ве­щественного сигнала это соответствует комплексному сопряжению спектра.

Дифференцирование сигнала

Посмотрим, как влияет на спектр дифференцирование сигнала во временной области. Для этого нам придется воспользоваться определением понятия произ­водной:

Применим к этому выражению преобразование Фурье:

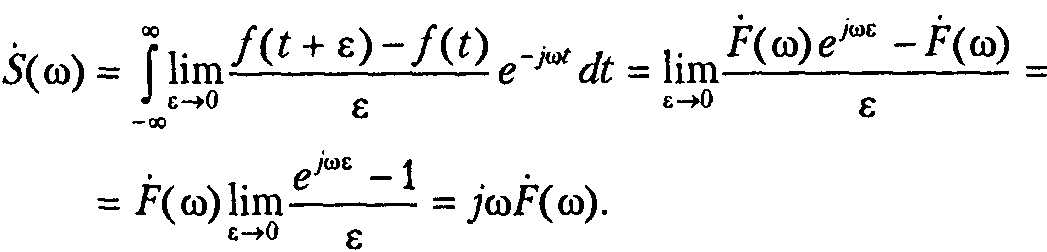
Спектр производной получается путем умножения исходного сигнала на j. Таким образом, при дифференцировании низкие частоты ослабляются, а высо­кие усиливаются. Фазовый спектр сигнала сдвигается на 90° для положитель­ных частот и на 90° для отрицательных.

Множитель j. называют оператором дифференцирования сигнала в частотной области.

Интегрирование сигнала

Интегрирование, как известно, является операцией, обратной дифференцирова­нию. Поэтому, исходя из результатов, полученных в предыдущем разделе, каза­лось бы, можно ожидать следующий результат:

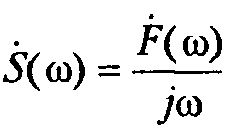
Однако все не так просто. Детальный анализ, выполненный, например, в [1], по­казывает, что эта формула справедлива лишь для сигналов, не содержащих по­стоянной составляющей, у которых

В общем же случае результат должен содержать дополнительное слагаемое в виде дельта-функции на нулевой частоте. Множитель перед дельта-функцией пропор­ционален постоянной составляющей сигнала:

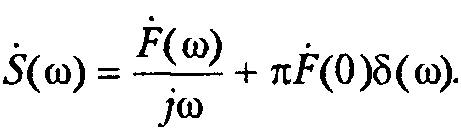
Итак, при интегрировании исходного сигнала высокие частоты ослабляются, а низкие усиливаются. Фазовый спектр сигнала смещается на -90° для положи­тельных частот и на 90° для отрицательных. Множитель 1/(j) называют опера­тором интегрирования в частотной области.

Спектр свертки сигналов

Свертка сигналов является очень часто используемой в радиотехнике интеграль­ной операцией, поскольку она описывает, в частности, прохождение сигнала че­рез линейную систему с постоянными параметрами (подробнее это будет обсуж­даться в главе 2):

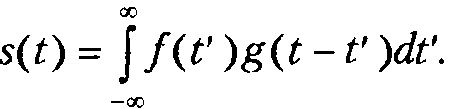
Подвергнем такую конструкцию преобразованию Фурье:

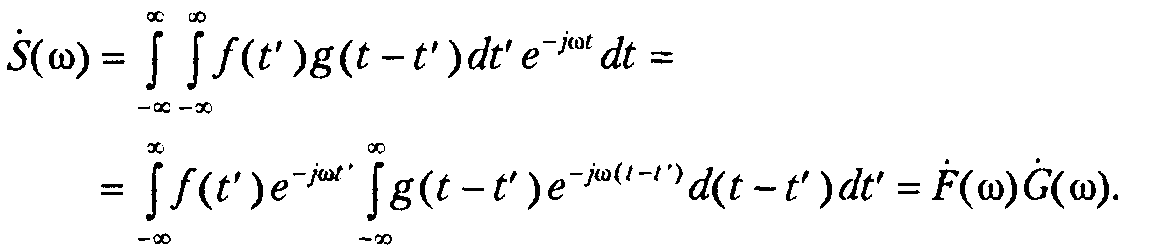
Полученный результат очень важен, он часто используется на практике: спектр свертки равен произведению спектров.

Спектр произведения сигналов

Дуальность преобразования Фурье и соотношение (1.16), полученное в преды­дущем разделе, позволяют легко предугадать результат. Однако все-таки полу­чим его:

тогда

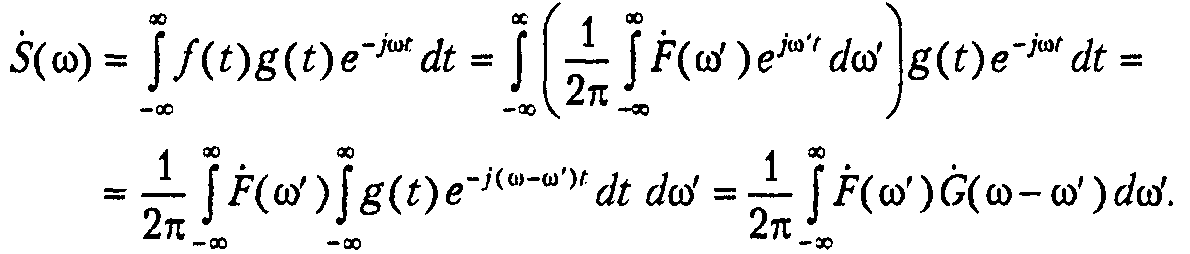
Как и следовало ожидать, спектр произведения представляет собой свертку спектров. Единственной дополнительной тонкостью является множитель 1/(2pi) перед интегралом свертки.

Таблица 1. Основные свойства НВПФ и функции

Свойство, функция	Функция	Преобразование
Линейность	ag( t ) + bh( t )	aG( f ) + bH( f )
Сдвиг по времени	h ( t - t0 )	H( f )exp( -j2pf t0 )
Сдвиг по частоте (модуляция)	h ( t )exp( j2pf0 t )	H( f - f0 )
Масштабирование	( 1 / |a| )h( t / a )	H( af )
Теорема свертки во временной области	g( t )*h( t )	G( f )H( f )
Теорема свертки в частотной области	g( t ) h( t )	G( f )*H( f )
Функция окна	Aw( t / T )	2ATsinc( 2Tf )
Функция sinc	2AFsinc( 2Ft )	Aw( f / F )
Импульсная функция	Ad( t )	A
Функция отсчетов	T(f)	FF(f), F=1/T