
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Ранг матрицы и системы линейных алгебраических уравнений
Пусть рассматривается система m
линейных алгебраических уравнений
с n неизвестными
![]()
 ( 16 )
( 16 )
Введем в рассмотрение две матрицы
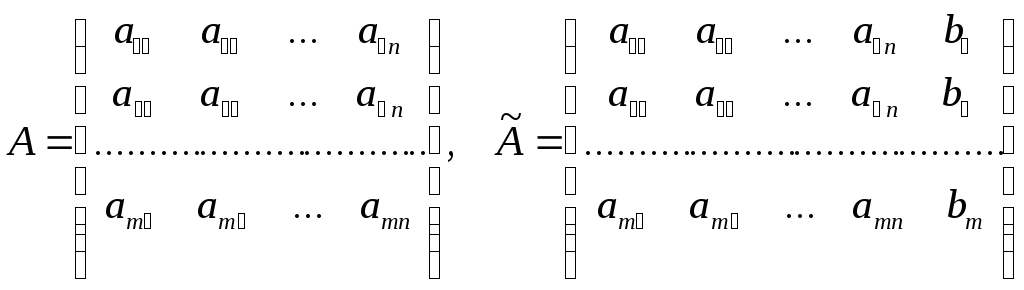 .
( 17 )
.
( 17 )
Первая образована коэффициентами при неизвестных и называется матрицей системы. Вторая отличается от первой дополнительным столбцом свободных членов и называется расширенной матрицей.
Очевидно,
![]() ,
( 18 )
,
( 18 )
то есть ранг матрицы системы A
не может быть больше ранга расширенной
ма-трицы
![]() .
.
Теорема (Кронекера4-Капелли5).
Система линейных алгебраических
ура-внений (16) совместна тогда и только
тогда, если ранг матрицы системы A
равен рангу расширенной матрицы
![]() ,
,
![]() .
( 19 )
.
( 19 )
Теорема Кронекера – Капелли определяет следующий план исследования системы уравнений (16).
-
Находим ранги матрицы системы A и расширенной матрицы
 .
Если
.
Если
![]() ,
,
система несовместна.
-
Рассмотрим теперь основной случай, когда
![]() ,
,
где k – некоторое
число. Очевидно,
![]() ,
то есть k не
превосходит ни чи-сла уравнений, ни
числа неизвестных.
,
то есть k не
превосходит ни чи-сла уравнений, ни
числа неизвестных.
На основании определения ранга матрицы
матрица А содержит по крайней мере
один отличный от нуля минор
![]() k-го порядка, а все
миноры высших порядков обеих матриц А
и
k-го порядка, а все
миноры высших порядков обеих матриц А
и
![]() равны нулю. Такой минор называется
базисным. Строки, в которых он
находится, определяют k
базисных уравнений данной системы
уравнений. Столбцы, в которых он находится,
определяют k базисных
неизвестных системы.
равны нулю. Такой минор называется
базисным. Строки, в которых он
находится, определяют k
базисных уравнений данной системы
уравнений. Столбцы, в которых он находится,
определяют k базисных
неизвестных системы.
Пусть, для определенности, базисный
минор
![]() расположен на пересечении первых k
строк и столбцов матрицы системы А,
то есть
расположен на пересечении первых k
строк и столбцов матрицы системы А,
то есть
 .
.
В этом случае базисными уравнениями и неизвестными являются первые k ура-внений и первые k неизвестных.
Если количество m
уравнений системы (16) превышает число
k, мы можем оставить
только k базисных
уравнений, а остальные
![]() уравнений отбросить, так как они, на
основании соответствующей теории,
которую мы во втузе не изучаем, являются
следствиями базисных уравнений. Таким
образом, мы должны рассматривать далее
систему только k
первых уравнений системы (16) с n
неизвестными. Могут представиться
два случая.
уравнений отбросить, так как они, на
основании соответствующей теории,
которую мы во втузе не изучаем, являются
следствиями базисных уравнений. Таким
образом, мы должны рассматривать далее
систему только k
первых уравнений системы (16) с n
неизвестными. Могут представиться
два случая.
А) Количество неизвестных n
равно k (![]() ),
то есть все неизвестные являются
базисными, и мы имеем систему k
уравнений с k
неизвестными и отличным от нуля
главным определителем
),
то есть все неизвестные являются
базисными, и мы имеем систему k
уравнений с k
неизвестными и отличным от нуля
главным определителем
![]() .
Такая система является сов-местной,
имеющей единственное решение, которое
мы можем найти одним из трех рассмотренных
выше методов (правило Крамера, метод
Гаусса или Жордана – Гаусса, матричный
метод).
.
Такая система является сов-местной,
имеющей единственное решение, которое
мы можем найти одним из трех рассмотренных
выше методов (правило Крамера, метод
Гаусса или Жордана – Гаусса, матричный
метод).
Б) Количество неизвестных n
превышает k (![]() ).
В этом случае k базисных
неизвестных мы оставляем слева, а
остальные
).
В этом случае k базисных
неизвестных мы оставляем слева, а
остальные
![]() неизвестных (так называемых свободных
неизвестных) переносим направо, считая
их произвольными. После этого мы решает
полученную систему уравнений относительно
базисных неизвестных (одним из только
что названных методов), то есть фактически
выражаем базисные неизвестные через
свободные. Система (16) является в этом
случае совместной, имеющей бесконечное
множество решений (так как свободные
неизвестные могут принимать какие
угодно значения), и мы получаем так
называемое общее решение системы.
неизвестных (так называемых свободных
неизвестных) переносим направо, считая
их произвольными. После этого мы решает
полученную систему уравнений относительно
базисных неизвестных (одним из только
что названных методов), то есть фактически
выражаем базисные неизвестные через
свободные. Система (16) является в этом
случае совместной, имеющей бесконечное
множество решений (так как свободные
неизвестные могут принимать какие
угодно значения), и мы получаем так
называемое общее решение системы.
Пример. Исследовать на совместность и решить систему линейных алгебраических уравнений

-
Матрица системы и расширенная матрица

имеют один и тот же ранг
![]() .
Ранг первой матрицы мы нашли выше, ранг
второй найдите самостоятельно.
Следовательно, данная система уравнений
совместна.
.
Ранг первой матрицы мы нашли выше, ранг
второй найдите самостоятельно.
Следовательно, данная система уравнений
совместна.
2. Выберем в качестве базисного минора
![]() (второго порядка) минор, расположенный
на пересечении первых двух строк и
столбцов матрицы системы А,
(второго порядка) минор, расположенный
на пересечении первых двух строк и
столбцов матрицы системы А,
![]() .
.
Такой выбор базисного минора определяет первые два уравнения и неизвестные как базисные.
Количество уравнений (![]() )
превышает число
)
превышает число
![]() ,
поэтому мы оставляем только базисные
уравнения данной системы, то есть сводим
ее к виду
,
поэтому мы оставляем только базисные
уравнения данной системы, то есть сводим
ее к виду
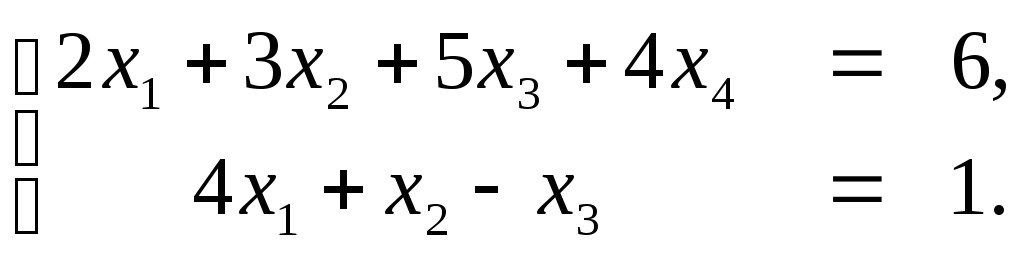
Количество неизвестных (![]() )
превышает число
)
превышает число
![]() ,
поэтому мы оставляем слева только
базисные неизвестные
,
поэтому мы оставляем слева только
базисные неизвестные
![]() ,
перенося направо свободные неизвестные
,
перенося направо свободные неизвестные
![]() ,
,

Полученную систему уравнений мы решаем
относительно
![]() методом Гаусса. Именно, прибавляя к
первому уравнению второе, предварительно
умно-женное на -3, получаем
методом Гаусса. Именно, прибавляя к
первому уравнению второе, предварительно
умно-женное на -3, получаем

откуда
![]() .
.
Ответ: общее решение данной системы уравнений имеет вид
![]() ,
,
где
![]() - произвольные числа.
- произвольные числа.
Замечание. Можно положить![]() и представить общее решение в несколько
иной форме, именно
и представить общее решение в несколько
иной форме, именно
![]() ,
,
где![]() -
произвольные числа.
-
произвольные числа.
Подчеркнем, что базисных миноров может быть несколько, и каждый из них определяет свои наборы базисных уравнений и неизвестных. Выбор базисного минора осуществляется самим студентом, решающим систему уравнений.
Пример. Исследовать на совместность уже рассматривавшуюся выше си-стему уравнений

Матрица системы и расширенная матрица здесь

Матрица А имеет отличный от нуля минор второго порядка
![]() .
.
Ее единственный минор третьего порядка (он же – и главный определитель данной системы уравнений)

Если
![]() ,
то
,
то
![]() ,
следовательно
,
следовательно
![]() ,
и система имеет единственное решение,
то есть она является совместной
определенной.
,
и система имеет единственное решение,
то есть она является совместной
определенной.
При
![]() обе матрицы принимают вид
обе матрицы принимают вид
 ,
,
ранг матрицы А равен 2, и нужно исследовать расширенную матрицу на ее ранг. Воспользуемся элементарными преобразованиями

Вот три первых из этих преобразований: а) третий столбец, умноженный на 3, 4 и -3, прибавляется соответственно к первому, второму и четвертому столбцам; б) первый столбец делится на 14, а второй – на 15; в) вторая строка, умноженная на -1, прибавляется к третьей. Далее подумайте самостоятельно.
Для последней из полученных выше матриц (неизменного ранга!) рассматриваем миноры второго и третьего порядков, а именно:

Таким образом, если
![]() ,
то
,
то
![]() ,
и система несовместна. Она является
совместной (и неопределенной) для
,
и система несовместна. Она является
совместной (и неопределенной) для
![]() ,
так как в этом случае
,
так как в этом случае
![]() .
.
