Матрицы

Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов, а именно:

( 7 )

В случае матрица называется квадратной n-го порядка.

Студенту необходимо повторить операции сложения матриц одинакового размера, умножения матрицы на число, умножения матриц, а также свойства этих операций. Здесь мы ограничимся одним примером на умножение матриц.

Пример. Найти произведения матриц

.

Первые две из них являются квадратными матрицами второго порядка, третья представляет собой матрицу-столбец, или матрицу размера .

Имеем

,

,

.

Важное значение для последующего имеет так называемая обратная мат-рица.

Матрица называется обратной для матрицы , если выполняется двойное матричное равенство

, ( 8 )

где E единичная матрица (у которой, как известно, все элементы главной диагонали – единицы, а остальные элементы равны нулю).

Обратная матрица данной квадратной матрицы с отличным от нуля определителем , или , находится с помощью простой формулы. Например, для квадратной матрицы третьего порядка

( 9 )

обратная матрица равна

, ( 10 )

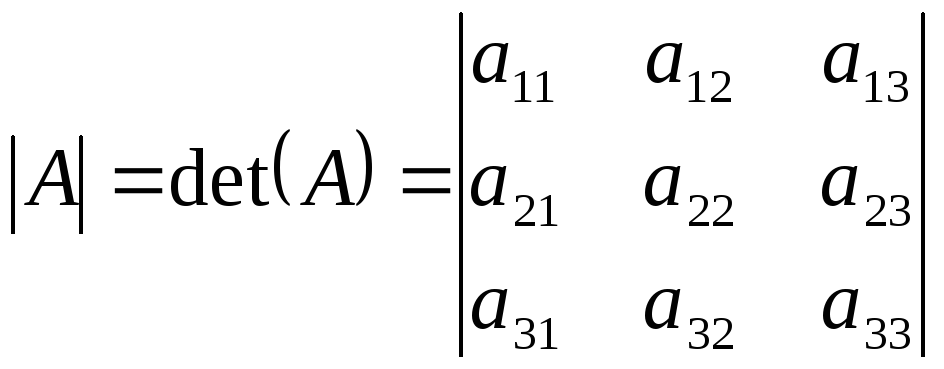. ( 11 )

Таким образом, обратная матрица матрицы находится по следующему правилу:

а) вычисляется определитель данной матрицы;

б) все элементы матрицы заменяются их алгебраическими дополнени-ями, и матрица алгебраических дополнений транспонируется;

в) полученная матрица делится на определитель данной матрицы.

Пример. Найти обратную матрицу для матрицы

.

а) Определитель матрицы равен

;

б) находим алгебраические дополнения всех элементов матрицы

следовательно, матрица алгебраических дополнений и ее транспонированная соответственно равны

, ;

в) искомая обратная матрица равна

.

Полученный результат необходимо проверить, а именно показать, что равенство (8), определяющее обратную матрицу, выполняется. Другими словами нужно доказать, что

Докажем первое равенство (второе докажите самостоятельно). Имеем:

.

Матричный метод решения систем линейных уравнений

Пусть задана система n линейных алгебраических уравнений с n неизвестными

( 12 )

и отличным от нуля главным определителем.

Введем в рассмотрение три матрицы

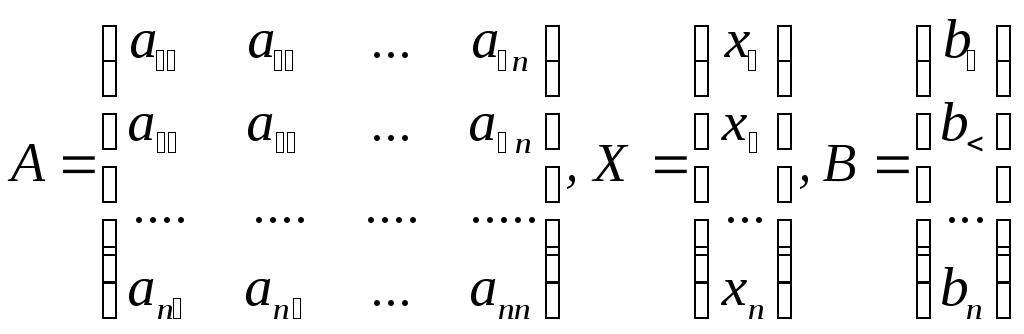. ( 13 )

Первая из них состоит из коэффициентов при неизвестных и называется матрицей системы. Вторая представляет собой матрицу-столбец неизвестных, а третья – матрицу-столбец свободных членов. Легко проверить, что система (12) может быть представлена в виде матричного уравнения

. ( 14 )

Последнее имеет, как известно, единственное решение

, ( 15 )

откуда получается искомое решение системы уравнений (12).

Описанный метод решения системы линейных алгебраических уравнений называется матричным.

Пример. Решить матричным способом систему уравнений

Матрица системы, матрицы-столбцы неизвестных и свободных членов здесь

.

Эквивалентное матричное уравнение и его решение

.

Обратная матрица матрицы A найдена выше,

,

следовательно,

.

Ответ: .