
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Аналитическая геометрия в пространстве уравнение поверхности
Определение. Уравнение вида
![]() ( 1 )
( 1 )
называется уравнением поверхности S, если координаты любой точки поверхности (и только такой точки) удовлетворяют ему.
 Пример.
Уравнение сферы
Пример.
Уравнение сферы
![]() радиуса R с центром
в точке
радиуса R с центром
в точке
![]() (рис. 1)
(рис. 1)
![]() .
( 2 )
.
( 2 )
Если центр сферы находится в начале
координат![]() ,
Рис. 1 ее уравнение принимает
вид
,
Рис. 1 ее уравнение принимает
вид
![]() .
( 3 )
.
( 3 )
Пример. Определить вид поверхности, заданной уравнением
![]() .
.
Дополняя до полных квадратов, получим
![]() ,
,
![]() ,
,
то есть уравнение сферы
![]() радиуса
радиуса
![]() с центром в точке
с центром в точке
![]() .
.
Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
Пусть плоскость
![]() (рис. 2) проходит через точку
(рис. 2) проходит через точку![]() и перпендикулярна некоторому ненулевому
вектору
и перпендикулярна некоторому ненулевому
вектору
![]() (так называемому нормальному вектору
плоскости).
(так называемому нормальному вектору
плоскости).
|
|
|
|
Так как для произвольной точки
![]() плоскости векторы
плоскости векторы
![]()
перпендикулярны, то их скалярное произведение равно нулю,
![]() ,
,
откуда следует уравнение плоскости
![]() .
( 4 )
.
( 4 )
Пример. Составить уравнение плоскости,
проходящей через данную точку
![]() параллельно двум векторам
параллельно двум векторам
![]() .
.
Если мы предположим, что векторы
![]() имеют общее начало
имеют общее начало![]() (рис.
3), то увидим, что нормальный вектор
плоскости коллинеарен их векторному
произведению,
(рис.
3), то увидим, что нормальный вектор
плоскости коллинеарен их векторному
произведению,
 ,
,
и с помощью уравнения (4) получим
![]() .
.
Замечание. Аналогичную задачу можно
рассмотреть в плоскости xOy:
составить уравнение прямой, проходящей
через точку
![]() перпендикулярно данному ненулевому
вектору (номальному вектору)
перпендикулярно данному ненулевому
вектору (номальному вектору)
![]() (рис. 4).
(рис. 4).
Аналогичные рассуждения приводят к следующему уравнению прямой:
![]() .
( 5 )
.
( 5 )
Раскрывая скобки, мы получим уравнение вида
![]() ,
( 6 )
,
( 6 )
где
![]() то есть общее уравнение прямой
то есть общее уравнение прямой
Если в уравнении (5) коэффициент
![]() ,
мы получаем уравнение прямой, проходящей
через точку
,
мы получаем уравнение прямой, проходящей
через точку
![]() и имеющей данный угловой коэффициент
k (или уравнение пучка
прямых с центром в точке
и имеющей данный угловой коэффициент
k (или уравнение пучка
прямых с центром в точке
![]() )
)
![]() .
( 7 )
.
( 7 )
 Пример.
Составить уравнение высоты, проведенной
из вершины C треугольника
ABC с задан-ными
вершинами
Пример.
Составить уравнение высоты, проведенной
из вершины C треугольника
ABC с задан-ными
вершинами![]() (рис. 5).
(рис. 5).
Нормальный вектор высоты
![]() ,
и на основании (5) имеем
Рис. 5
,
и на основании (5) имеем
Рис. 5
![]() .
.
Общее уравнение плоскости
Уравнение (4) после раскрытия скобок может быть записано в виде
![]()
где
![]() и
и
![]() .
Обратно, уравнение
.
Обратно, уравнение
![]() (
(![]() )
( 8 )
)
( 8 )
является уравнением плоскости с
нормальным вектором
![]() .
Оно называется общим уравнением
плоскости.
.
Оно называется общим уравнением
плоскости.
Некоторые частные случаи общего уравнения плоскости
1. Если
![]() ,
то плоскость, уравнение которой принимает
вид
,
то плоскость, уравнение которой принимает
вид
![]() ,
,
проходит через начало координат
![]() .
.
2. Если
![]() ,
то плоскость с соответствующим уравнением
,
то плоскость с соответствующим уравнением
![]()
параллельна оси Ox.
3. Если
![]() ,
плоскость, уравнение которой
,
плоскость, уравнение которой
![]() ,
,
параллельна осям Ox,
Oy и, следовательно,
параллельна плоскости xOy.
Если, кроме того,
![]() ,
получаем уравнение плоскости xOy,
а именно:
,
получаем уравнение плоскости xOy,
а именно:
![]() .
( 9 )
.
( 9 )
Аналогично рассматриваются другие
случаи общего уравнения плоскости, в
частности (если
![]() или
или
![]() ),
мы приходим к уравнениям плоскостей
xOz, yOz
),
мы приходим к уравнениям плоскостей
xOz, yOz
![]() ( 10 )
( 10 )

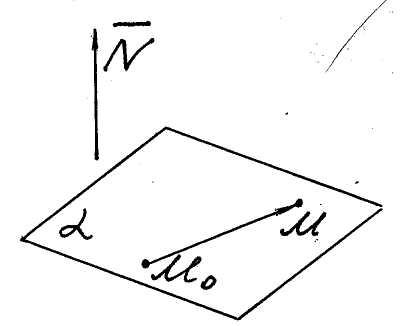 Fig. 2
Fig. 2 Fig. 3
Fig. 3 Fig. 4
Fig. 4