Вопросы для самопроверки по теме "Определители"

1. Сформулировать определение определителя 2-го порядка.

2. Сформулировать определение определителя 3-го порядка

3. Дать определение минора элемента определителя.

4. Записать произвольно по одному определителю второго и третьего порядков и вычислить миноры всех их элементов.

5. Дать определение алгебраического дополнения элемента определителя.

6. Записать произвольно по одному определителю второго и третьего порядков и вычислить алгебраические дополнения всех их элементов.

7. Сформулировать свойство "Создатель нулей" определителя.

8. Сформулировать свойство о разложении определителя по элементам его строки или столбца.

9. Как можно вычислить определитель четвертого порядка, умея вычислять определители третьего порядка?

10. Как можно вычислить определитель пятого порядка, умея вычислять определители четвертого порядка?

11. Сформулировать свойство определителя – теорему Лагранжа.

12. Перечислить все свойства определителей.

Системы линейных алгебраических уравнений.

Рассмотрим систему трех линейных алгебраических уравнений с тремя неизвестными

( 3 )

Здесь - известные коэффициенты, - также известные свободные члены, а - неизвестные, которые требуется найти.

Решением системы (3) называется упорядоченная тройка чисел, которая удовлетворяет каждому ее уравнению.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.

Имеется много способов решения системы (3). Сейчас мы рассмотрим так называемое правило Крамера.

Правило Крамера1

Введем в рассмотрение главный определитель системы (3)

и три вспомогательных определителя

Главный определитель образован из коэффициентов при неизвестных, а первый (второй, третий) вспомогательный определитель получается из главного определителя заменой его первого (соответственно второго, третьего) столбца стол-бцом свободных членов.

Теорема (правило) Крамера. Если главный определитель системы (3) отличен от нуля, то система совместна и имеет единственное решение, которое находится по следующему правилу:

. ( 4 )

Аналогичное правило справедливо для системы произвольного количества n линейных алгебраических уравнений с n неизвестными.

Пример. Решить систему линейных уравнений

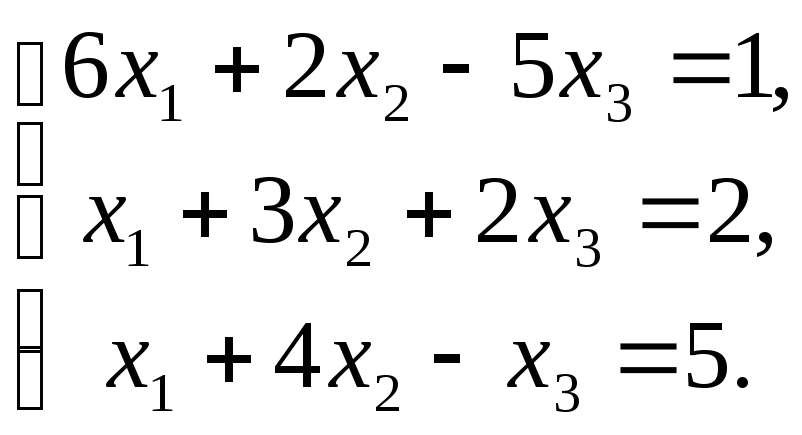
Главный и вспомогательный определители системы равны

Следовательно, на основании правила Крамера (4) получаем единственное решение системы

.

Ответ: .

Пример. При каких значениях параметров a и b система трех линейных алгебраических уравнений с тремя неизвестными

а) имеет единственное решение; б) не имеет решений; в) имеет бесконечное множество решений.

Решение. Главный определитель системы

,

и система имеет единственное решение при .

Пусть теперь . Система уравнений принимает следующий вид

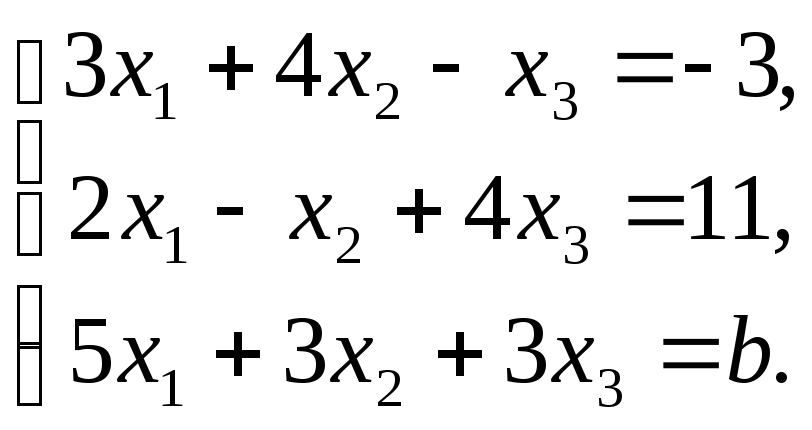
Ее главный определитель равен нулю, а вспомогательные определители равны

.

Так как (эти три равенства вытекают из доказательства правила Крамера), то при

и

система уравнений не имеет решений. Если же

и ,

то из тех же равенств следует, что система имеет бесконечное множество решений.