Смешанное произведение трех векторов14

Смешанным произведением трех векторов называется скалярное произведение векторного произведения первых двух векторов на третий.

Если векторы заданы в декартовом ортонормированном базисе , то есть если

,

то их смешанное произведение равно определителю третьего порядка, в первой строке которого находятся координаты первого вектора, во второй - координаты второго, в третьей – координаты третьего,

. ( 23 )

Пример. Смешанное произведение векторов

на основании формулы (23) равно

.

Из формулы (23) и свойств определителей вытекают два следующих соотношения, касающиеся возможности переставлять местами сомножители смешанного произведения:

На основании формулы (17) для скалярного произведения мы можем записать следующую формулу для смешанного произведения:

.

Из нее, в частности, вытекает

Геометрический смысл смешанного произведения. Абсолютная величина смешанного произведения векторов равна объему параллелепипеда, построенного на этих векторах как на сторонах,

=. ( 24 )

Действительно, площадь основания и высота такого параллелепипеда соответственно равны

, ,

откуда следует формула (24).

Условие компланарности трех векторов. Три ненулевых вектора компланарны тогда и только тогда, если их смешанное произведение равно нулю.

Пример. Векторы пре-дыдущего примера компланарны, так как их смешанное произве-дение равно нулю.

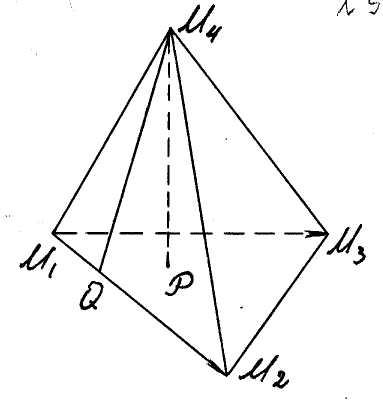
Пример. Найти объем треугольной пирамиды с вершинами

, Рис. 10 и длину ее высоты , опущенной из вершины (рис. 10).

Введем в рассмотрение векторы

.

Данная пирамида построена на них как на сторонах. Ее объем равен шестой части объема параллелепипеда, построенного на тех же векторах как на сторонах. Следовательно, на основании формулы (24)

куб.единиц

Длину высоты находим, исходя из известной школьной формулы. Именно:

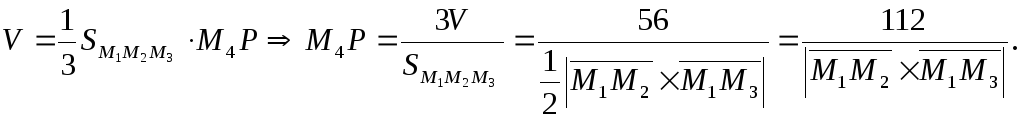
Так как

получаем

лин.единиц.

Вопросы для самопроверки по теме "Векторы"

1. Что такое вектор и его орт?

2. Дать определение равных векторов; противоположных векторов.

3. Какие векторы называются коллинеарными? компланарными?

4. Как можно определить сумму векторов? разность векторов? произведение вектора на число?

5. Что такое составляющая вектора вдоль оси? проекция вектора на ось?

6. По какой формуле можно найти проекцию вектора на ось?

7. Что такое базис на плоскости? в пространстве?

8. Что такое декартов ортонормированный базис?

9. Сформулировать теорему о разложении вектора по базису.

10. Что такое координаты вектора в данном базисе? что представляют собой координаты вектора в декартовом ортонормированном базисе?

11. Какая существует связь между линейными операциями над векторами и операциями над их координатами?

12. Сформулировать необходимое и достаточное условие коллинеарности двух векторов; (не)компланарности трех векторов.

13. Как найти координаты вектора, зная координаты его начала и конца?

14. Как найти длину, направляющие косинусы и орт вектора, заданного в декартовом ортонормированном базисе?

15. Перечислите основные способы задания векторов.

16. Дать определение скалярного произведения двух векторов.

17. Какая существует связь между скалярным произведением и проекцией вектора на ось?

18. Перечислите свойства скалярного произведения.

19. Как найти скалярное произведение векторов, заданных в декартовом ортонормированном базисе?

20. Как найти угол между двумя векторами с помощью скалярного произведения?

21. Как найти проекцию вектора на ось с помощью скалярного произведения?

22. Дать определение правой тройки векторов.

23. Дать определение векторного произведения двух векторов.

24. В чем состоит геометрический смысл модуля (длины) векторного произведения?

25. Перечислите свойства векторного произведения.

26. Как найти векторное произведение векторов, заданных в правом декартовом ортонормированном базисе?

27. Дать определение смешанного произведения трех векторов.

28. Как найти смешанное произведение векторов, заданных в декартовом ортонормированном базисе?

29. В чем состоит геометрический смысл смешанного произведения?