
- •Донецк 2009
- •Методические указания к индивидуальному заданию: элементы линейной алгебры и аналитической геометрии линейная алгебра определители
- •Вопросы для самопроверки по теме "Определители"
- •Системы линейных алгебраических уравнений.
- •Правило Крамера1
- •Метод Гаусса2
- •Матрицы
- •Матричный метод решения систем линейных уравнений
- •Ранг матрицы
- •Ранг матрицы и системы линейных алгебраических уравнений
- •Системы линейных однородных уравнений
- •Собственные значения и собственные векторы матрицы
- •Вопросы для самопроверки по темам "Системы линейных уравнений" и "Матрицы"
- •Аналитическая геометрия на плоскости прямая и окружность Уравнение линии. Окружность
- •Уравнение прямой с угловым коэффициентом
- •Общее уравнение прямой
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой в отрезках, отсекаемых ею на координатных осях
- •Взаимное расположение двух прямых Угол между двумя прямыми
- •Условия параллельности и перпендикулярности прямых
- •Дальнейшие примеры
- •Кривые второго порядка
- •Гипербола
- •Парабола
- •Полярные координаты
- •Переход от декартовых прямоугольных координат к полярным и наоборот
- •Уравнения некоторых линий в полярных координатах
- •Преобразование координат
- •Способы задания кривых
- •Вопросы для самопроверки по теме "Аналитическая геометрия на плоскости"
- •Векторы
- •Проекция вектора на ось
- •Разложение вектора по базису
- •Декартов ортонормированный базис
- •Скалярное произведение двух векторов
- •Векторное произведение двух векторов
- •Смешанное произведение трех векторов14
- •Вопросы для самопроверки по теме "Векторы"
- •Аналитическая геометрия в пространстве уравнение поверхности
- •Плоскость Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору
- •Общее уравнение плоскости
- •Некоторые частные случаи общего уравнения плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Уравнение плоскости в отрезках
- •Расстояние от точки до плоскости
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности
- •Задача о пересечении трех плоскостей
- •Пространственная прямая Уравнения прямой, проходящей через данную точку параллельно заданному вектору
- •Уравнения прямой, проходящей через две данные точки
- •Общие уравнения прямой
- •Угол между двумя прямыми Условия параллельности и перпендикулярности
- •Плоскость и пространственная прямая Пересечение прямой с плоскостью (и поверхностью)
- •Угол между пространственной прямой и плоскостью Условия параллельности и перпендикулярности
- •Вопросы для самопроверки по теме "Аналитическая геометрия в пространстве"
- •Содержание
Декартов ортонормированный базис
В приложениях наиболее часто используется
так называемый декартов ортонормированный
базис. В пространстве - это тройка
единичных (или нормированных) взаимно
перпендикулярных (ортогональных)
векторов, обычно обозначаемых
![]() ,
а в плоскости - аналогичная пара векторов
,
а в плоскости - аналогичная пара векторов
![]() .
Система координат, определяемая
декартовым ортонормированным базисом,
называется декартовой прямоугольной.
.
Система координат, определяемая
декартовым ортонормированным базисом,
называется декартовой прямоугольной.
Координаты вектора, разложенного по
декартовому ортонормированному базису,
представляют собой проекции этого
вектора на соответствующие координатные
оси и соответствующим образом обозначаются.
Так, если для пространственного вектора
![]() имеем следующее разложение по
имеем следующее разложение по
![]() :
:
![]() ,
( 8 )
,
( 8 )
то
![]() .
.
Используя формулу (1) для нахождения проекции вектора на ось, имеем
![]() ,
( 9 )
,
( 9 )
где
![]() - углы, образованные вектором
- углы, образованные вектором
![]() соответственно с осями
соответственно с осями
![]()
![]() .
.
В частности,
![]() ,
а поэтому
,
а поэтому
![]() .
Аналогично
.
Аналогично
![]() .
.
Из формул (9) следует, что если вектор образует с какой-либо осью острый (тупой) угол, то соответствующая координата вектора положительна (соответственно отрицательна).
Например, вектор
![]() образует с осью
образует с осью
![]() тупой угол, а с осями
тупой угол, а с осями
![]() - острые углы.
- острые углы.
Длина (модуль) вектора, заданного в декартовом ортонормированном базисе, равна квадратному корню из суммы квадратов его координат. Именно,
![]() ( 10 )
( 10 )
для вектора (8), заданного в базисе
![]() ,
и
,
и
![]()
для вектора, заданного в базисе
![]() .
.
Косинусы углов
![]() ,
образованных вектором (8) с координатными
осями, называются направляющими. На
основании формулы (9) они равны
,
образованных вектором (8) с координатными
осями, называются направляющими. На
основании формулы (9) они равны
![]() .
( 11 )
.
( 11 )
Из формул (11) и (10) следует, что сумма квадратов направляющих косинусов равна единице,
![]() ,
( 12 )
,
( 12 )
а поэтому орт вектора (8) определяется следующей формулой:
![]() .
( 13 )
.
( 13 )
В свою очередь вектор может быть представлен с помощью своих длины и орта, а именно:
![]() ( 14 )
( 14 )
Пример. Найти расстояние между точками
![]() .
.
Достаточно найти длину вектора
![]() :
:
![]() .
(15)
.
(15)
Пример. Вектор![]() задан в декартовом ортонормированном
базисе
задан в декартовом ортонормированном
базисе
![]() своим началом
своим началом
![]() и концом
и концом
![]() .
Найти вектор, его длину, орт, направляющие
косинусы, расстояние между точками A
и B.
Затем найти вектор
.
Найти вектор, его длину, орт, направляющие
косинусы, расстояние между точками A
и B.
Затем найти вектор
![]() ,
имеющий длину 12 и направленный
противоположно вектору
,
имеющий длину 12 и направленный
противоположно вектору
![]() ,
а также вектор
,
а также вектор
![]() длины 20, сонаправленный с вектором
длины 20, сонаправленный с вектором
![]() .
.
По формуле (5)
![]()
Пользуясь теперь формулами (10), (15), (11), (13), (14), последовательно получаем
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Скалярное произведение двух векторов
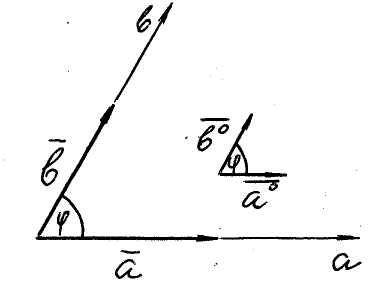 Как
известно, скалярным произведением
двух векторов называется чи-сло, равное
произведению длин (модулей) этих векторов
на косинус угла между ними, то есть (см.
рис. 3)
Как
известно, скалярным произведением
двух векторов называется чи-сло, равное
произведению длин (модулей) этих векторов
на косинус угла между ними, то есть (см.
рис. 3)
![]() .
( 16 )
.
( 16 )
Пример. Скалярное произведение векторов
![]() ,
Рис. 3 имеющих длины
,
Рис. 3 имеющих длины
![]() и образующих угол
и образующих угол
![]() ,
равно
,
равно
![]()
Скалярное произведение равно произведению длины одного вектора на проекцию другого на первый (или, точнее, на ось, определяемую первым вектором),
![]() ,
( 17 )
,
( 17 )
где a, b
– оси, определенные векторами
![]() соответственно.
Формула (17) следует из определения (16) и
формулы (1) для нахождения проекции
вектора на ось.
соответственно.
Формула (17) следует из определения (16) и
формулы (1) для нахождения проекции
вектора на ось.
Пример. Проекции каждого из векторов предыдущего примера на ось другого на основании формулы (17) соответственно равны
![]() .
.
Необходимо хорошо знать свойства
скалярного произведения: 1) перестановочность
(![]() ),
2) сочетательность относительно скалярного
(в том числе числового) множителя (
),
2) сочетательность относительно скалярного
(в том числе числового) множителя (![]() ),
3) распределительность относительно
векторных сомножителей (
),
3) распределительность относительно
векторных сомножителей (![]() ).
Особо отметим два следующих свойства:
).
Особо отметим два следующих свойства:
4)
![]() ,
( 18 )
,
( 18 )
то есть скалярный квадрат вектора равен квадрату его длины;
5) Два ненулевых вектора перпендикулярны (ортогональны) тогда и только тогда, если их скалярное произведение равно нулю.
Пример. Скалярные произведения векторов
декартового ортонормированного базиса
![]() равны
нулю,
равны
нулю,
![]() ,
,
так как
![]() .
.
Пример. Длины векторов
![]() равны
равны
![]() ,
угол между ними
,
угол между ними
![]() .
Найти длину вектора
.
Найти длину вектора
![]() .
.
На основании свойств скалярного произведения, в том числе формулы (18),

Если векторы заданы в декартовом
ортонормированном базисе
![]() ,
то их скалярное произведение равно
сумме произведений их соответствующих
координат, то есть если
,
то их скалярное произведение равно
сумме произведений их соответствующих
координат, то есть если
![]() ,
,
или просто
![]() ,
,
то
![]() .
( 19 )
.
( 19 )
 Пример.
Является ли прямоугольным треугольник
с данными вершинами
Пример.
Является ли прямоугольным треугольник
с данными вершинами
![]()
![]() ?
Найти его внутренний и внешний углы при
вершине A (рис. 4).
?
Найти его внутренний и внешний углы при
вершине A (рис. 4).
Стороны треугольника ABC равны
![]()
![]() ,
,
Рис. 4 причем
![]() .
Поэтому треугольник не является
прямоугольным. Для нахождения упомянутых
углов введем векторы
.
Поэтому треугольник не является
прямоугольным. Для нахождения упомянутых
углов введем векторы
![]() .
.
Используя формулы (16) и (19), мы получаем
![]()
![]()
![]()
Пример. Найти вектор
![]() ,
удовлетворяющий условиям
,
удовлетворяющий условиям
![]() ,
,
где
![]() - данные векторы.
- данные векторы.
Пусть искомый вектор имеет координаты
![]() ,
то есть
,
то есть
![]() .
Тогда
.
Тогда
![]()
и решение задачи сводится к
решению системы линейных уравнений
относительно
![]() ,
,

Эта последняя была решена в первой части настоящего пособия, а именно:
![]() .
.
Ответ: Искомый вектор
![]() .
.
