Уравнение прямой в отрезках, отсекаемых ею на координатных осях

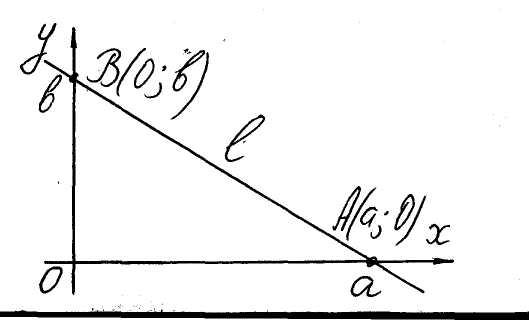
Пусть прямая l отсекает отрезки OA, OB на осях Ox, Oy (соответственно) и (см. рис. 10). В таком случае уравнение прямой может быть Рис. 10 записано в виде

. ( 16 )

Пример. Найти площадь треугольника, ограниченного координатными осями и прямой .

Сведем уравнение прямой к виду (16),

.

Тогда искомая площадь будет равна

(квадратных единиц).

Взаимное расположение двух прямых Угол между двумя прямыми

Пусть даны две прямые с известными угловы-ми коэффициентами (рис. 11). Угол Рис. 11 между ними определяется по формуле

. ( 17 )

Пример. Найти угол между двумя прямыми линиями, заданными их общими уравнениями: .

Находя угловые коэффициенты прямых, применяем формулу (17).

Условия параллельности и перпендикулярности прямых

Формула (17) позволяет установить необходимое и достаточное условия параллельности и перпендикулярности двух прямых.

Две прямые параллельны тогда и только тогда, если равны их угловые коэффициенты,

. ( 18 )

Две прямые перпендикулярны тогда и только тогда, если их угловые коэффициенты удовлетворяю условию

. ( 19 )

Пример. Составить уравнение прямой, проходящей через вершину треугольника параллельно его стороне BC.

Угловой коэффициент k искомой прямой равен . Формума (15) дает

,

и на основании формулы (12) имеем

.

Пример. Составить уравнение высоты, опущенной из вершины A того же треугольника ABC.

Если мы обозначим угловой коэффициент искомой высоты, то на основании условия (19) перпендикулярности двух прямых будем иметь

,

откуда найдем

.

Теперь записываем уравнение высоты, применяя уравнение (12),

.

Дальнейшие примеры

Пример. Найти точку Q, которая симметрична точке относите-льно прямой, проходящей через две данные точки (рис. 12).

Fig. 12

Fig. 13

Fig. 14

Найти расстояние точки от прямой AB.

1. Составляем уравнение прямой AB (на основании формулы (14))

.

2. Составим уравнение прямой PQ, которая перпендикулярна прямой AB и проходим через точку . На основании условия перпендикулярности прямых

.

Теперь на основании уравнения (12) получаем

.

3. Находим точку M пересечения прямых PQ и AB. Решая соответствующую систему уравнений

получаем .

4. Для нахождения искомой точки Q примем во внимание, что найденная точка является серединой отрезка PQ, а следовательно

.

Таким образом, мы нашли искомую точку .

5. Для нахождения расстояния точки от прямой AB достаточно найти расстояние между точками и ,

Пример. Даны вершины треугольника ABC (см. рис. 13). Составьте самостоятельно уравнения его высоты BD, медианы CE и биссектрисы BF. Составить далее уравнение окружности, описанной около треугольника.

Пусть точка является центром описанной окружности. Это значит, что

Мы получили систему уравнений относительно координат точки . Возводя в квадрат и приводя подобные члены, сводим систему к системе линейных уравнений

.

Квадрат радиуса окружности равен

,

Откуда получаем приближенное уравнение описанной окружности

.

Пример. Даны две вершины и точка пересечения высот треугольника ABC (рис. 14). Найти координаты вершины C.

Решение.

1. Имея точки , по формуле (15) находим угловой коэффициент высоты AK:

2. Используя условие перпендикулярности прямых, находим угловой коэффициент стороны BC,

3. С помощью уравнения (12) составляем уравнение прямой BC:

4. Таким же путем составляем уравнение прямой AC:

5. Находим точку C пересечения прямых BC, AC , решая систему урав-нений этих прямых.

Замечание. Расстояние точки от прямой l, заданной общим уравнением

,

может быть найдено с помощью следующей формулы:

. ( 20 )

Пример. Составить уравнение окружности с центром , которая касается прямой .

Радиус окружности равен расстоянию точки от данной прямой. Находим его с помощью формулы (20),

.

Теперь составляем искомое уравнение окружности,