Вариант III (все длины указаны в см)

1. Прямоугольные треугольники ABC и A′B′C′ подобны. Если B = = 28°, то треугольник A′B′C′ имеет угол, равный

1) 152° 2) 62° 3) 52° 4) 64°

2. В треугольниках ABC и A′B′C′ C =C′, AC = 4, A′C′ = 8. Если B′C′ = 2BC, то отношение AB : A′B′ равно

1) 1/2 2) 2 3) 4 4) 1/4

3. Вписанный угол содержит 130°. Градусная мера дуги, на которую он опирается, равна

1) 65° 2) 130° 3) 220° 4) 260°

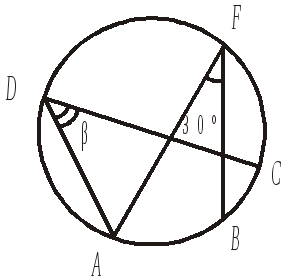
4. На дугу AB опирается вписанный угол, содержащий 30°. Если вписанный угол ADC равен β, то 1) β < 30° 2) β = 30° 3) β > 30° 4) β зависит от положения точки D на дуге AF

5. Сумма внутренних углов выпуклого многоугольника 1080°. Тогда число сторон многоугольника равно

1) 6 2) 7 3) 8 4) 9

6. Внешний угол правильного шестиугольника равен

1) 30° 2) 60° 3) 72° 4) 54°

7. В окружность вписан прямоугольник со сторонами 8 и 6. Найдите радиус этой окружности. 1) 5 2) 6 3) 4 4) 10

8. Укажите ложное утверждение.

1) Любые две окружности подобны.

2) Любые два отрезка подобны.

3) Любые два квадрата подобны.

4) Любые два ромба подобны.

9. В треугольнике ABC A = 45°, AB = 2, AC = 1. Найдите BC.

1) 13 2) 3) 5 4)

10. В треугольнике ABC BC = 9, AB = 6, sin C =1/6. Найдите sin A.

1) 2) 3) 4)

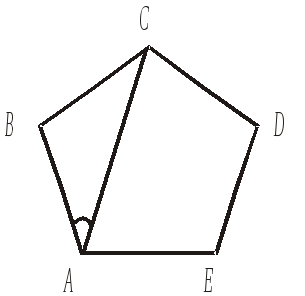
11. ABCDE – правильный пятиугольник. Найдите BAC. 1) 15° 2) 18° 3) 36° 4) 30°
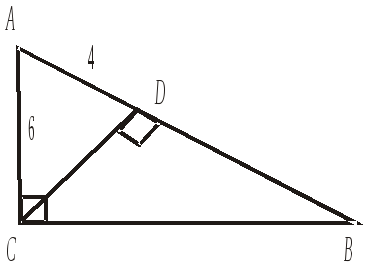
12. В треугольнике ABC C =D = 90°, AC = 6, AD = 4. Найдите гипотенузу AB. 1) 18 2) 13 3) 12 4) 9
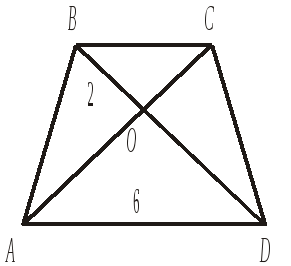
13. В трапеции ABCD AD || BC, AD = 6, BC = 3. Если BO = 2, то диагональ BD равна 1) 4 2) 9 3) 5 4) 6

14. Около треугольника ABC описана окружность с центром в точке O. Если A = 65°, B = 35°, то

1) Точка o лежит на одной из сторон треугольника.

2) Точка o лежит вне треугольника.

3) Точка o лежит внутри треугольника.

4) положение точки O определить нельзя.

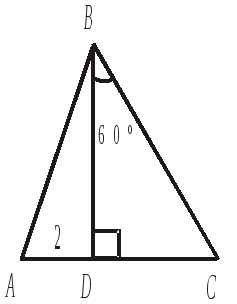
15. В треугольнике ABC BD AC, ABC = = 105°. Если DBC = 60°, AD = 2, то отрезок DC равен 1) 2 2) 2 3) 3 4) 3

16. Сторона правильного многоугольника равна 8. Если радиус вписанной в него окружности 4, то радиус описанной окружности равен

1) 12 2) 6 3) 8 4) 8

17. Сторона ромба равна 3. Если одна из диагоналей равна 2, то косинус тупого угла ромба равен

1) 2) 3) 4)

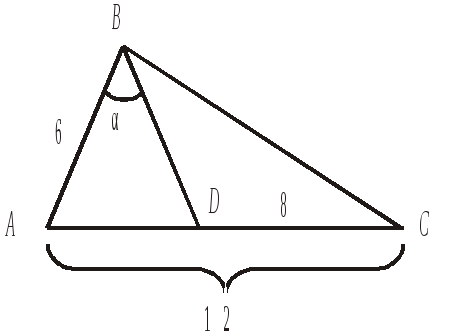
18. В треугольнике ABC BD – биссектриса угла B, ABD = α. Если AB = 6, AC = = 12, DC = 8, то A равен 1) 2α 2) 90° – α 3) α 4) 90° – 2α