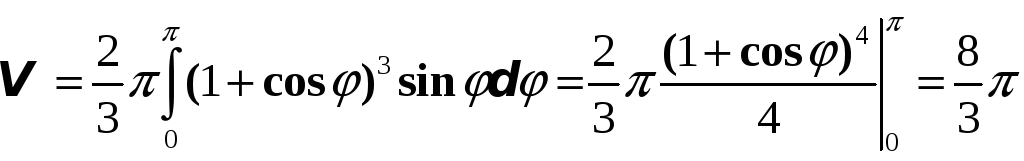Типовой расчет

I курс (модуль 3)

Неопределенные и определенные интегралы

2007

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

Типовые Расчеты по Высшей математИке

1 Курс (Модуль 3)

Неопределенные и определенные интегралы

Методические указания и задачи для студентов

Санкт-Петербург

2007

Типовые расчеты по высшей математике. 1курс (модуль 3). Неопределенные и определенные интегралы. Составители: Попов И.Ю., Тесовская Е.С., Блинова И.В. / Методическое пособие. СПб: СПбГУ ИТМО, 2007. 35 с.

В пособии приведены типовые расчеты с методическими указаниями по теме «Неопределенный и определенный интегралы».

Пособие предназначено для студентов первого курса всех специальностей и направлений СПбГУ

Рекомендовано к печати Советом естественнонаучного факультета (протокол N2 от 18 сентября 2007 г.)

В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных образовательных программ вузов России на 2007–2008 годы. Реализация инновационной образовательной программы «Инновационная система подготовки специалистов нового поколения в области информационных и оптических технологий» позволит выйти на качественно новый уровень подготовки выпускников и удовлетворить возрастающий спрос на специалистов в информационной, оптической и других высокотехнологичных отраслях экономики.

Санкт-Петербургский государственный

университет информационных

технологий, механики и оптики, 2007

И.Ю.Попов,Е.С.Тесовская, Блинова И.В. 2007

Методические указания

Типовой расчет содержит семь заданий.

В заданиях I и II предлагается найти неопределенные интегралы, используя их простейшие свойства, такие, как линейность, и основные приемы интегрирования – замену переменной (или внесение под знак дифференциала) и интегрирование по частям. Напомним указанные свойства.

Линейность:

1. .

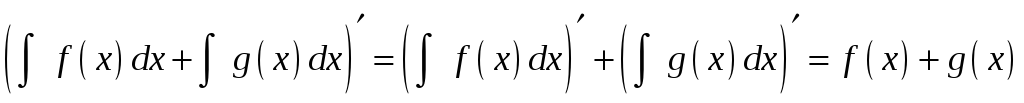2. .

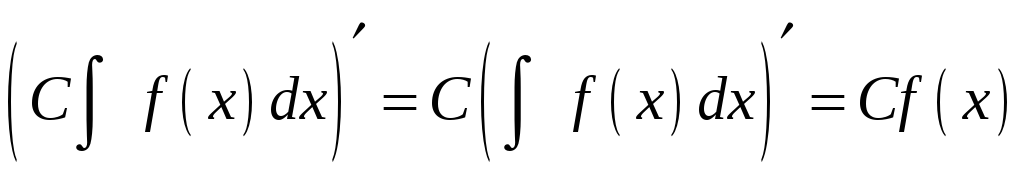Пример 1. Найти .

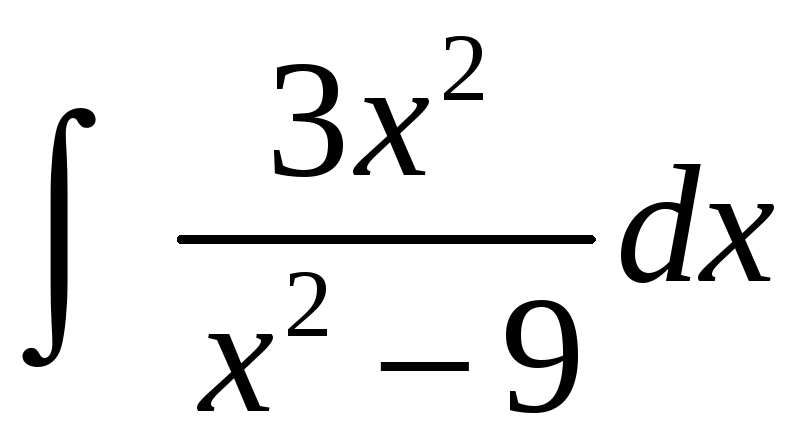Решение. Преобразуя подынтегральное выражение в сумму, и используя свойство линейности интеграла, получим сумму двух табличных интегралов:

.

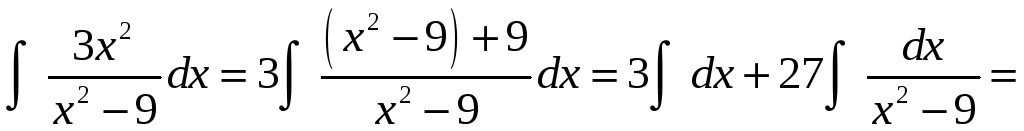
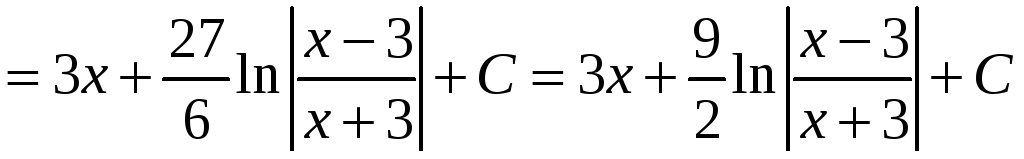Теорема (замена переменной в неопределенном интеграле):

Пусть функция является первообразной для функции на некотором промежутке и функция непрерывная и имеет непрерывную производную на промежутке , причем для всякого значения выполняется неравенство . Тогда будет справедлива формула:

(*),

где .

Формулу (*) можно применять, не вводя явно новой переменной. В общем виде она будет выглядеть следующим образом: . Тогда, если - первообразная функции , то . Такой прием называют внесением под знак дифференциала.

Пример 2. Найти , .

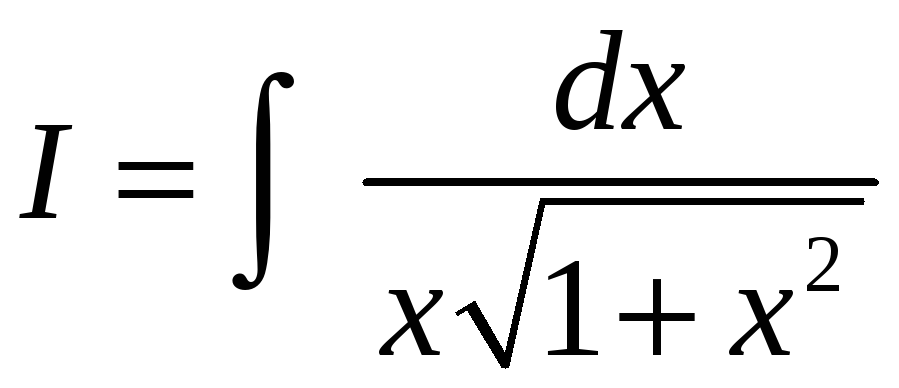Решение.

Первый способ. Приведем пример применения формулы *.

Пусть требуется найти интеграл , .

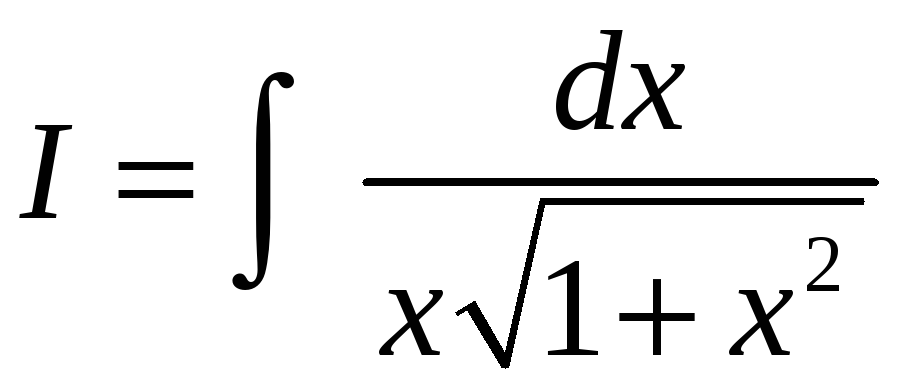Сделаем замену переменной , то есть . Чтобы применить формулу, нужно сделать замену переменной в подынтегральной функции и положить .

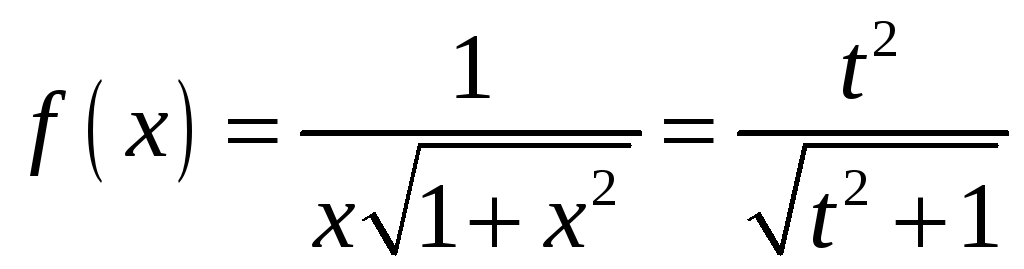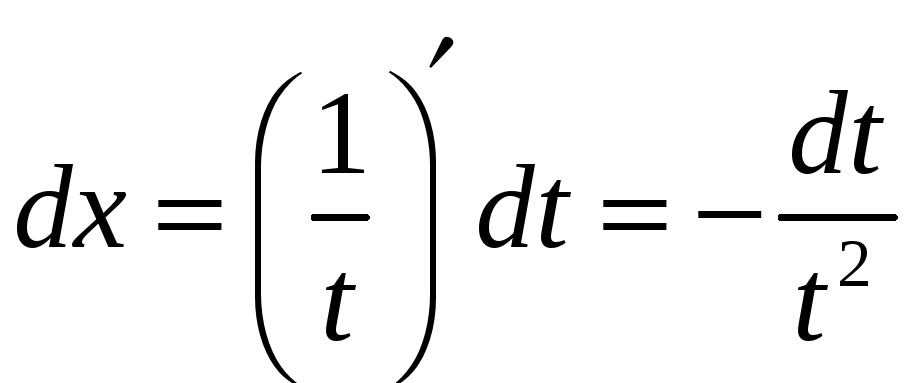В нашем интеграле и . Тогда .

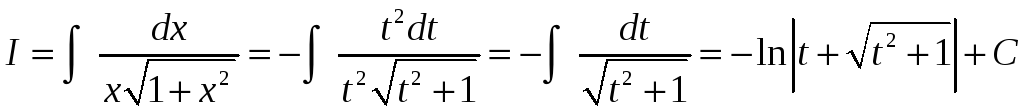Делая замену , получим окончательно .

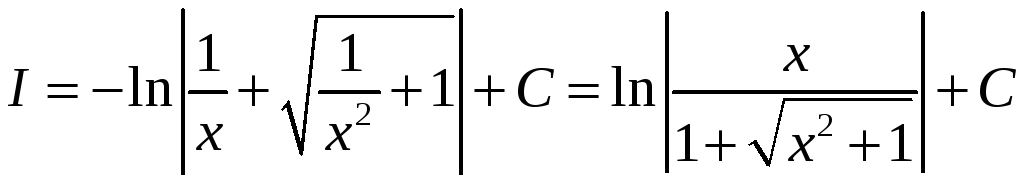Второй способ. Сделаем замену переменной по формуле .

Тогда . Для того, чтобы выразить через , продифференцируем равенство :

.

Тогда .

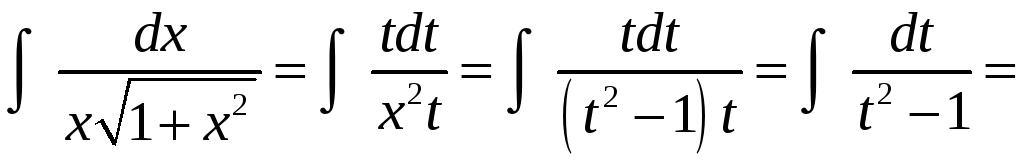
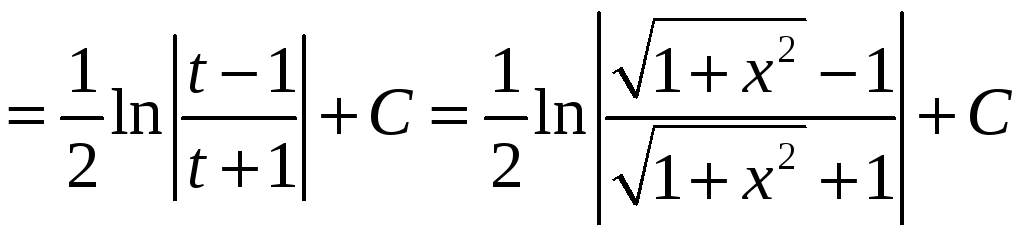Замечание. Чтобы доказать равенство ответов, полученных обоими способами, можно во втором ответе избавиться от иррациональности в числителе и вынести показатель степени за знак логарифма:

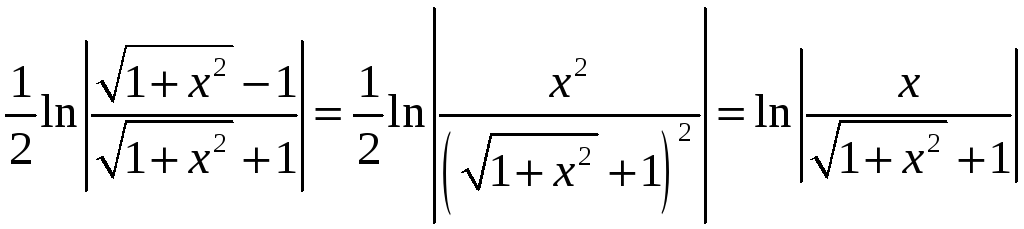
Одним из основных приемов при поиске первообразной является интегрирование по частям. Формула интегрирования по частям имеет вид

.

Приведем пример использования формулы.

Пример 3. Найти интеграл .

Решение. Возьмем и применим формулу интегрирования по частям. Для этого сначала надо вычислить и v: и .

Тогда .

Замечания.

1. При нахождении функции v находят не все первообразные, а только одну из них, поэтому произвольную постоянную С писать не надо; в примере было .

2. Очевидно, основная трудность применения этой формулы состоит в том, чтобы правильно выбрать компоненты интеграла u и dv. Обычно этот метод применяется, когда под знаком интеграла имеется трансцендентная функция, такая как и т.п. Тогда можно руководствоваться следующим правилом: если производная от трансцендентной функции становится функцией алгебраической (т.е. рациональной или иррациональной дробью), то за u принимается эта функция. Например, в интеграле за u надо взять , так как , то есть после дифференцирования получается дробь.

Если же трансцендентность после дифференцирования не исчезает, то эту функцию включают в состав dv, например, в предыдущем примере за u был взят множитель х, а функция была включена в dv: .

В задании III требуется найти интеграл от рациональной функции. Опишем указанную процедуру, приведя основную теорему.

1. Рациональной дробью называется выражение вида 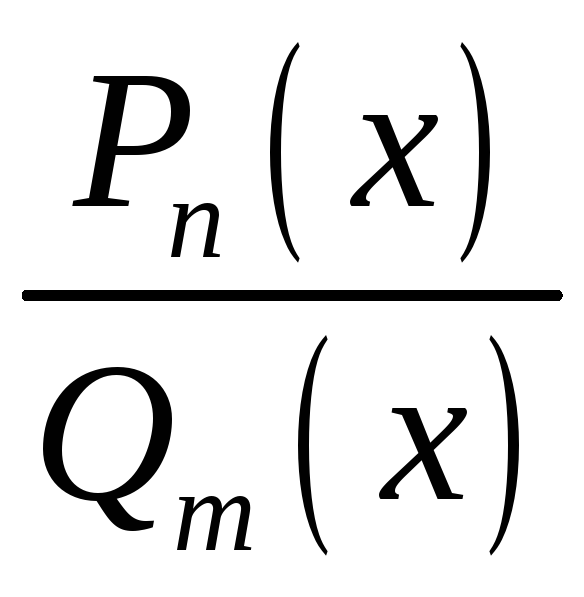, где и многочлены от переменной х степени n и m соответственно.

Например, дроби 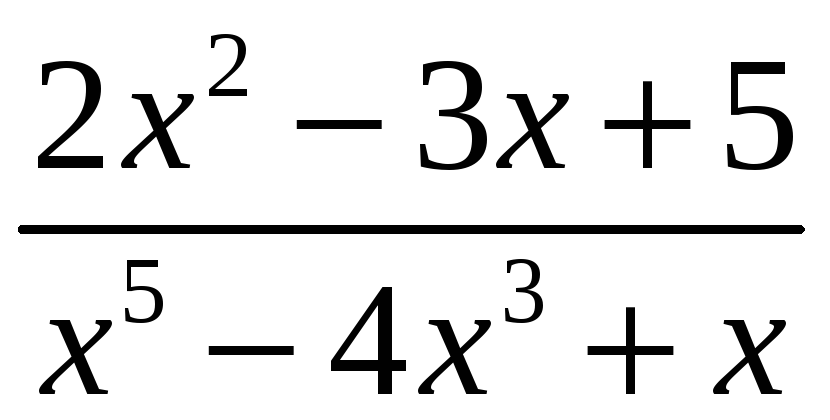, , 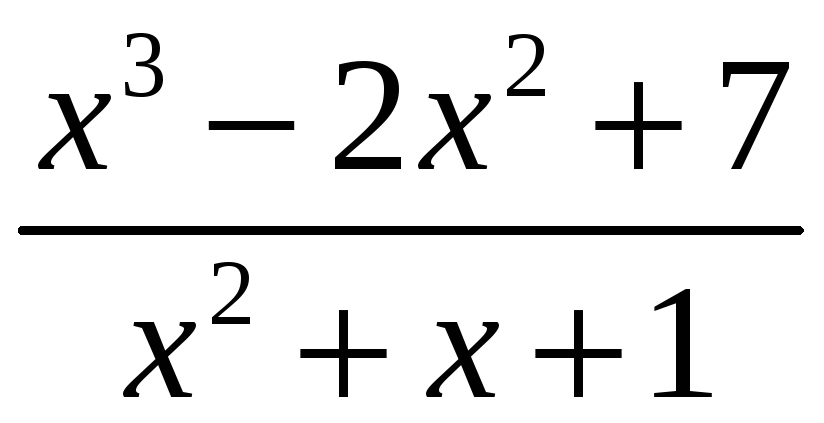являются рациональными дробями относительно переменной х.

2. Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, строго меньше степени многочлена, стоящего в знаменателе. В противном случае дробь называется неправильной.

В предыдущих примерах первая дробь будет правильной, а две последние неправильными.

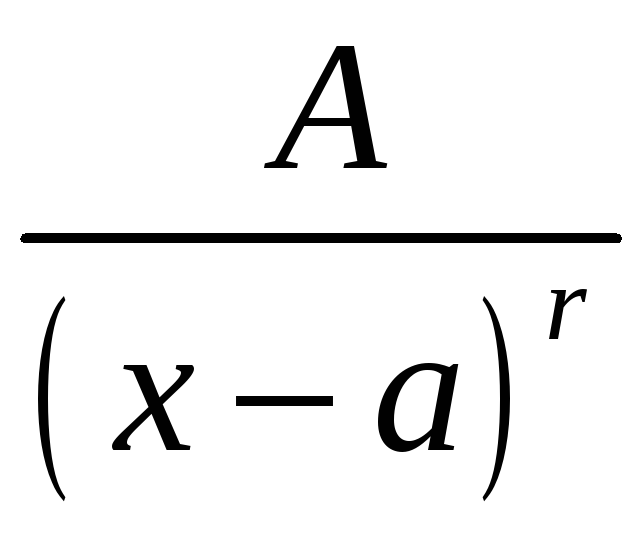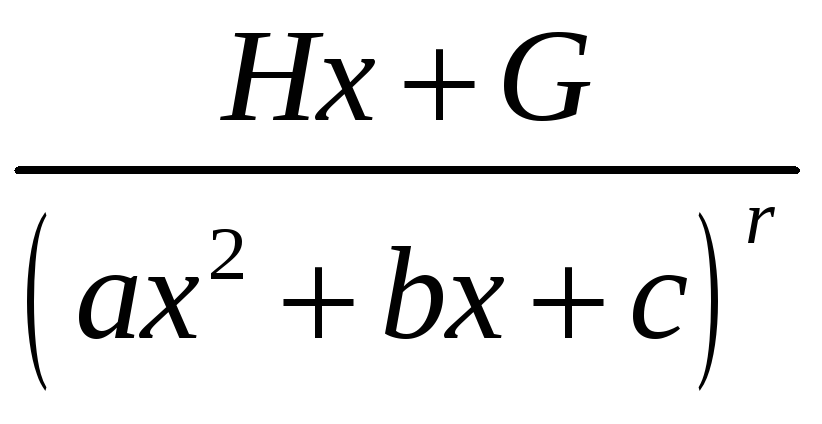3. Простейшими дробями будем называть дроби вида , , и , где дискриминант квадратного трехчлена, стоящего в знаменателях двух последних дробей, строго меньше нуля, то есть эти знаменатели нельзя разложить на вещественные простые множители.

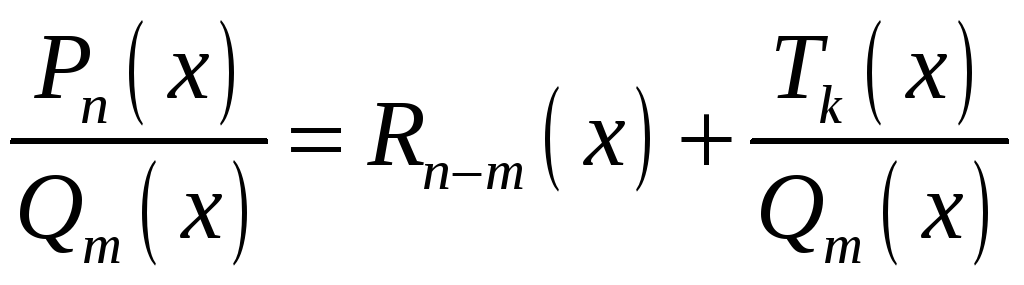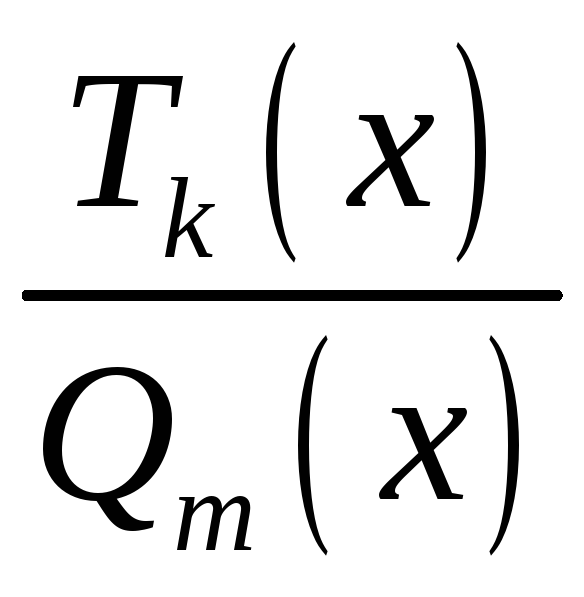Если дробь неправильная, то из нее можно выделить целую часть, то есть представить дробь в виде , где многочлен степени n-m, а - многочлен степени , то есть дробь - правильная. Чтобы получить такое представление дроби, надо разделить числитель на знаменатель с остатком. Тогда многочленом будет неполное частное, а остаток от деления.

Правильную дробь всегда можно представить в виде суммы простейших дробей.

Теорема о разложении правильной рациональной дроби в сумму простейших дробей.

Пусть дробь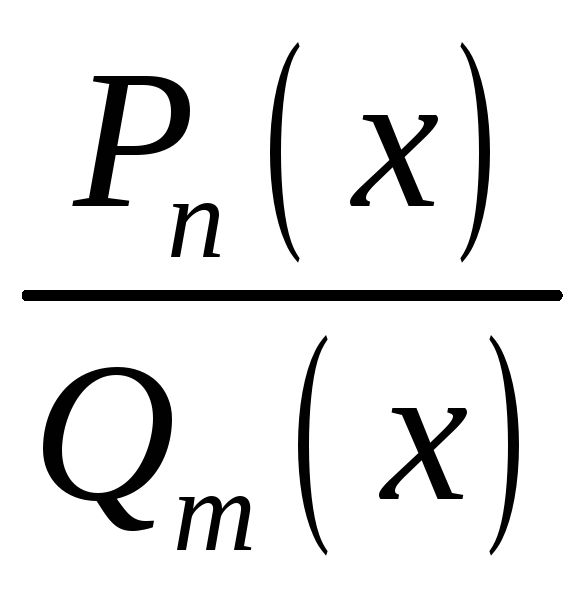 - правильная, несократимая и многочлен разложен на множители в области вещественных чисел, то есть , где все квадратные трехчлены не имеют вещественных корней. Тогда

.

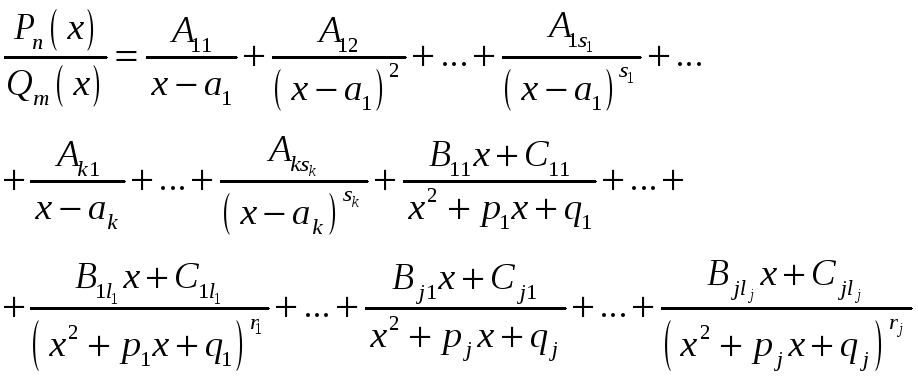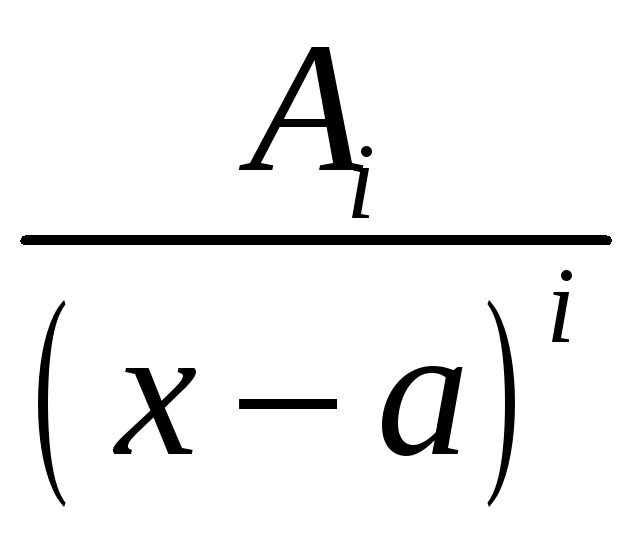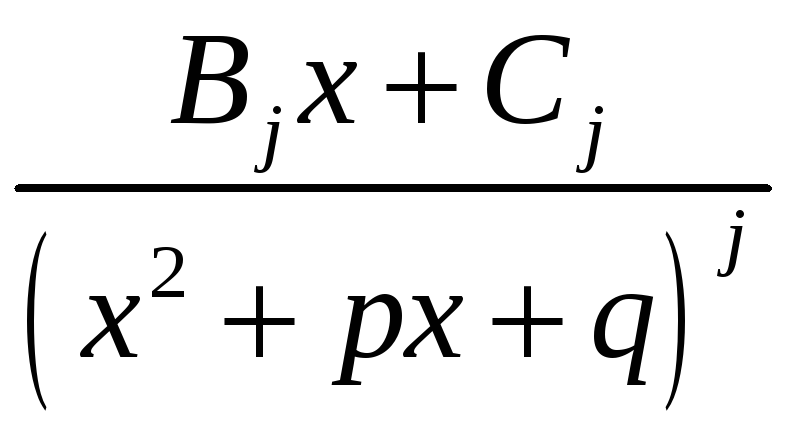Замечание. Теорема утверждает, что каждая правильная дробь раскладывается на сумму простейших дробей в соответствии с разложением на множители знаменателя. Каждому множителю вида соответствует k дробей вида , где показатель i меняется от 1 до s, и в числителях стоят некоторые константы , и каждому множителю вида соответствуют m дробей вида , где показатель j меняется от 1 до r, а в числителях стоят линейные функции .

Рассмотрим теперь интеграл .

Чтобы его вычислить, достаточно руководствоваться несколькими правилами:

1) Если дробь 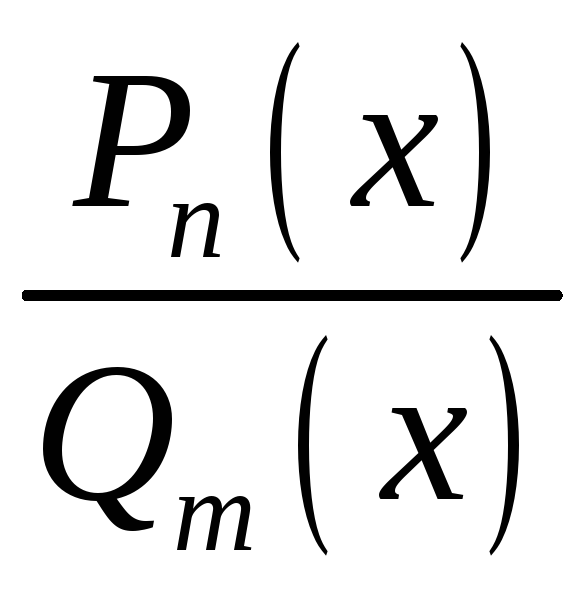неправильная, то из нее надо выделить целую часть. Последняя является многочленом, следовательно, легко интегрируется, поэтому проблема сводится к интегрированию правильной дроби.

2) Правильную дробь надо разложить на сумму простейших дробей. Тогда интеграл от этой дроби сведется к сумме интегралов от простейших дробей.

Как нам известно*, простейшие дроби бывают четырех типов: 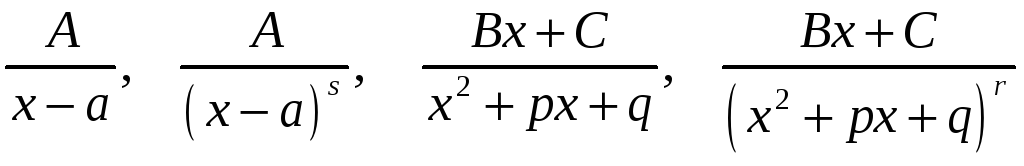. Первые две из них интегрируются подведением под знак дифференциала:

.

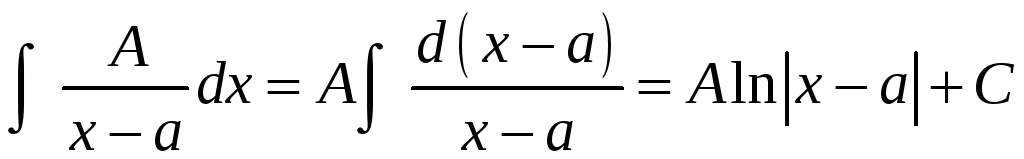
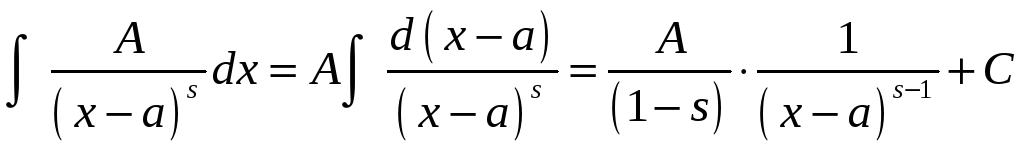Интегрирование третьей дроби мы уже рассматривали*.

Рассмотрим интегрирование простейшей дроби четвертого типа. Сначала выделим полный квадрат в знаменателе этой дроби: 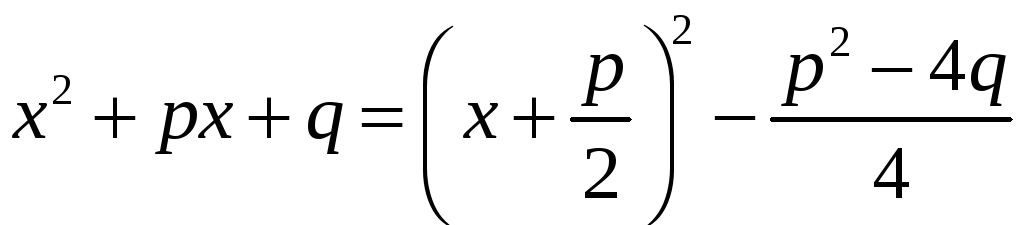. Так как дискриминант квадратного трехчлена отрицателен, то 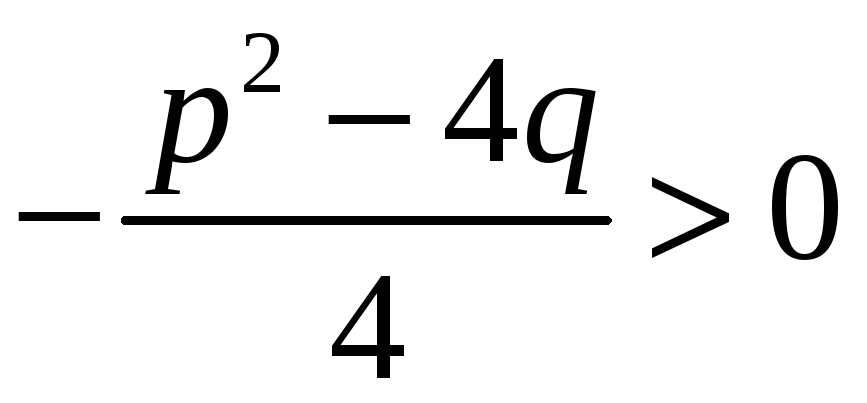, поэтому можно ввести обозначение 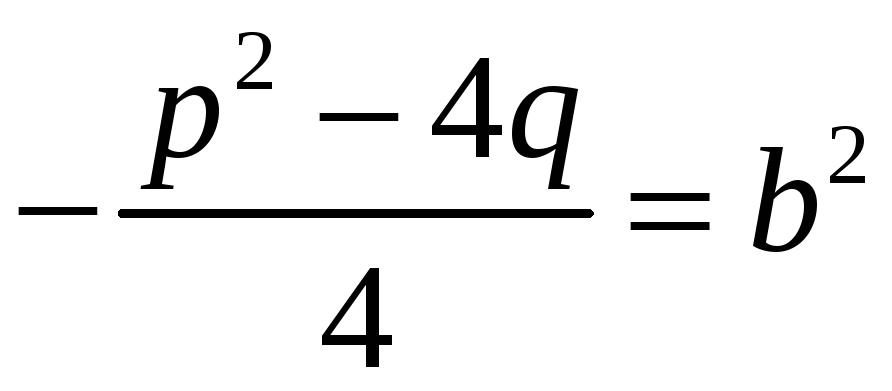. Кроме того, введем замену переменной . Тогда ,

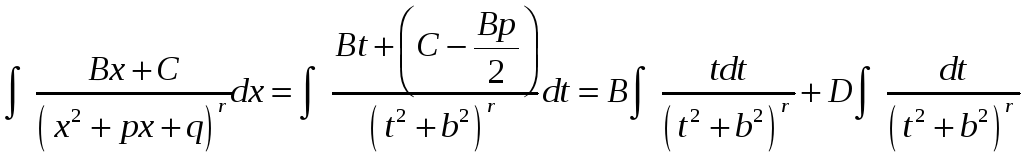где . Первый из полученных интегралов берется подведением под знак дифференциала:

.

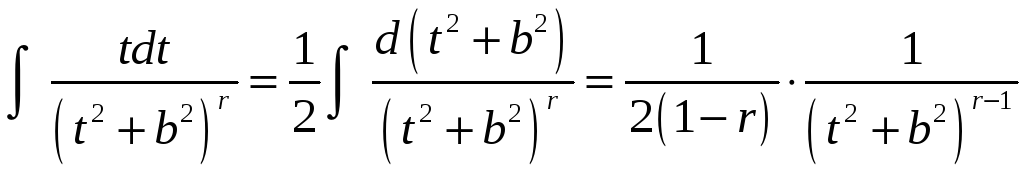Что касается второго интеграла, то к нему применяется прием, называемый понижением степени. Обозначим этот интеграл через . Сначала преобразуем числитель этого интеграла

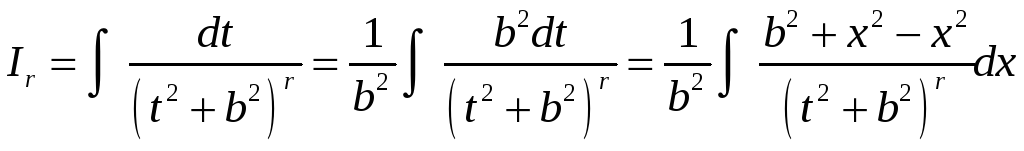
и разобьем его на два слагаемых .

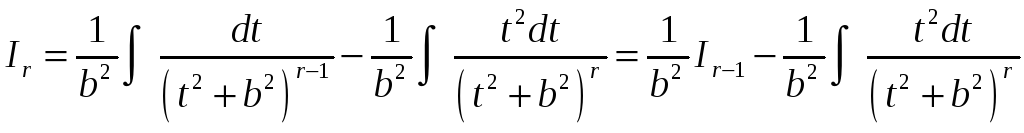Последний интеграл проинтегрируем по частям, положив .

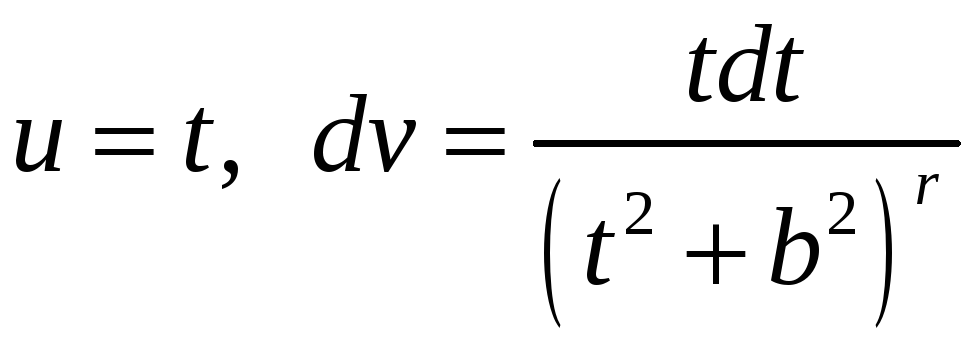Тогда ,

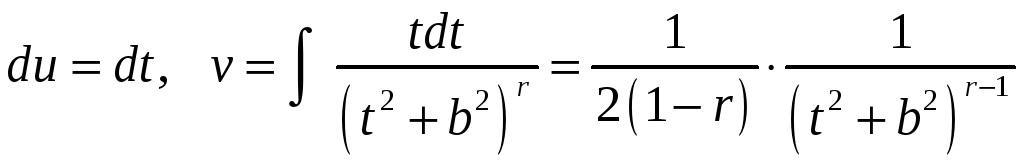Откуда

.

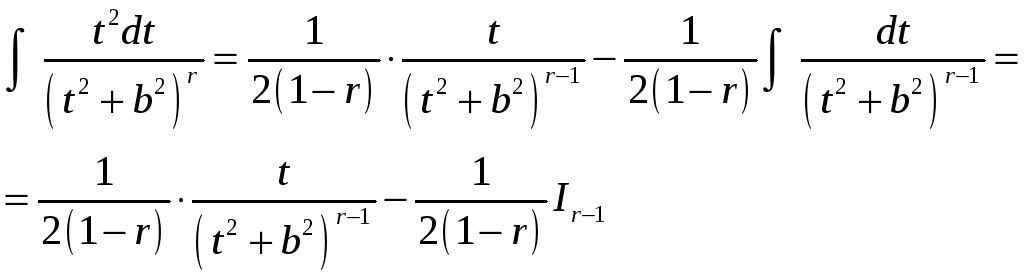Окончательно получим

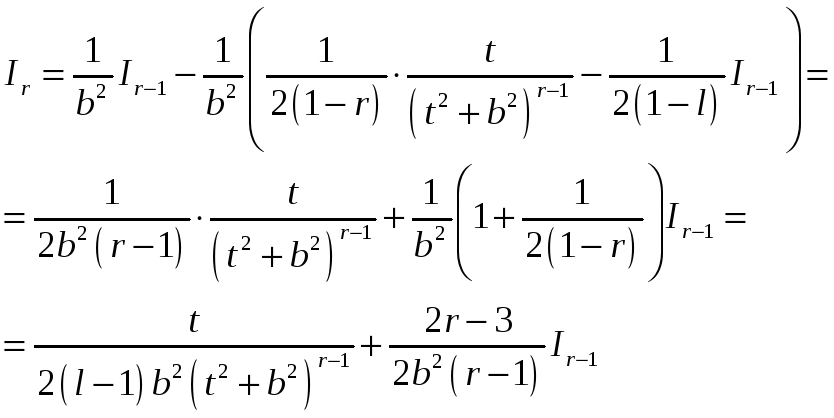
Формула 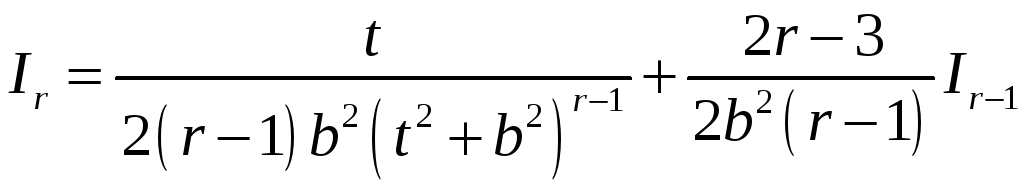называется рекуррентной формулой и ею можно пользоваться при вычислении подобных интегралов, но так как эту формулу трудно выучить наизусть, предпочтительнее при вычислении таких интегралов пользоваться тем приемом, с помощью которого эта формула была получена.

В дальнейшем мы узнаем еще один способ вычисления подобного интеграла.

Рассмотрим несколько примеров.

Пример 4. Вычислить .

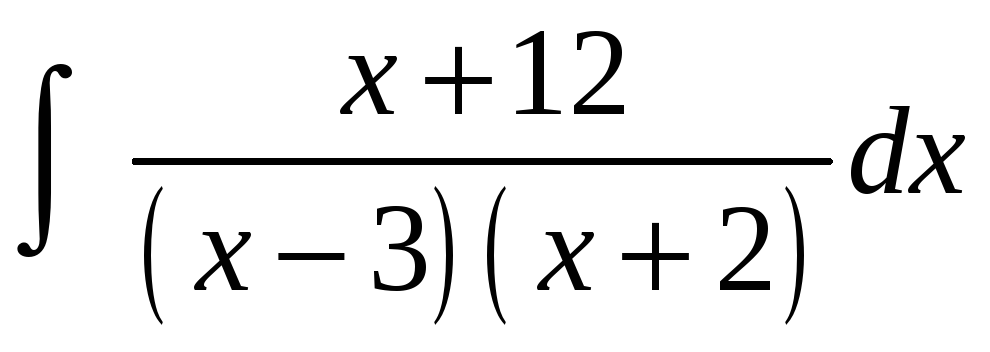Решение. Дробь, стоящую под знаком интеграла, представим в виде суммы простейших дробей с неопределенными коэффициентами: 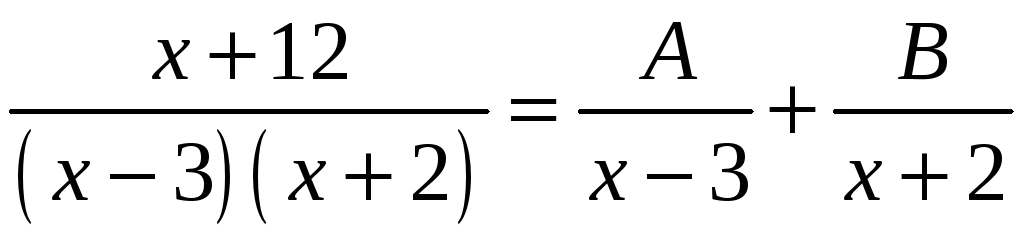. Чтобы найти коэффициенты разложения, снова приведем сумму этих простейших к общему знаменателю. Тогда 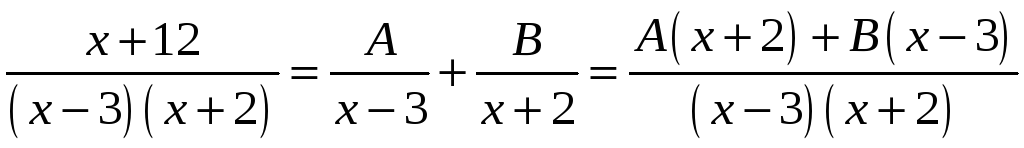. Сравним первую дробь этого равенства с последней. Так как знаменатели этих дробей равны, то должны быть равны и числители, т. е. . Теперь для нахождения неопределенных коэффициентов можно воспользоваться одним из двух критериев равенства двух многочленов:

1) Два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях.

2) Два многочлена равны тогда и только тогда, когда значения этих многочленов равны при любом значении переменной х.

В этом примере воспользуемся первым критерием равенства многочленов. Раскрывая скобки, получим . В многочленах справа и слева приравняем коэффициенты при х и свободные члены. Получится система 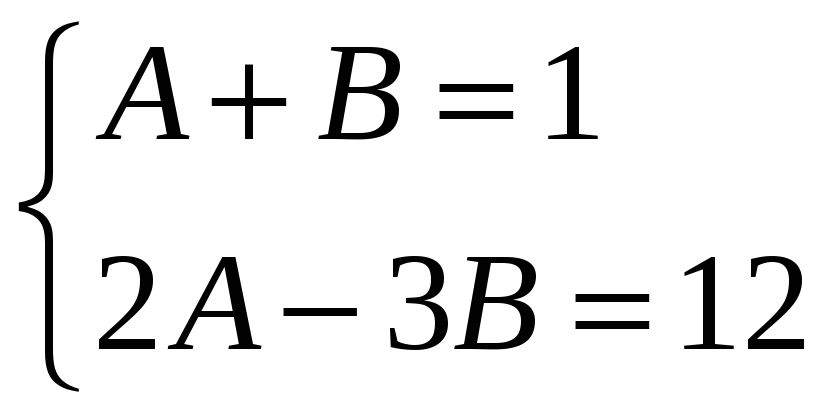, решая которую, находим А=3 и В=-2.

Тогда .

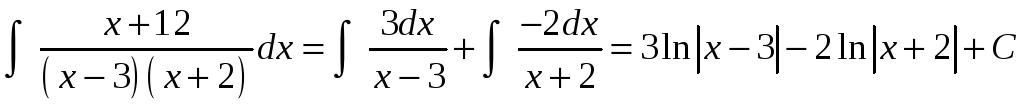Пример 5. Вычислить .

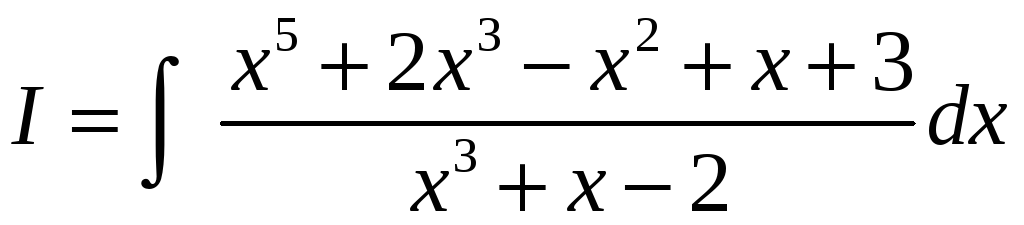Решение. Дробь, стоящая под интегралом, неправильная, поэтому из нее надо выделить целую часть. Это можно сделать делением числителя на знаменатель уголком

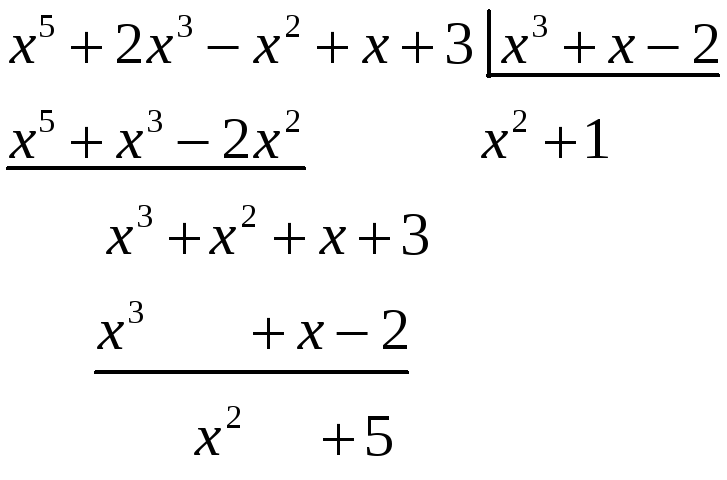
Отсюда

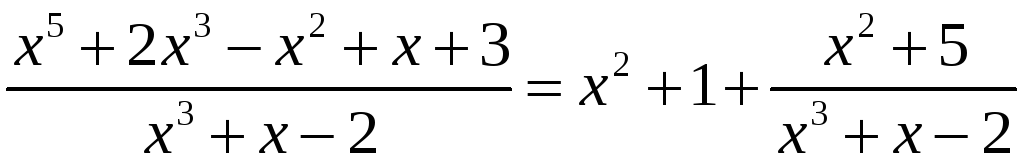и .

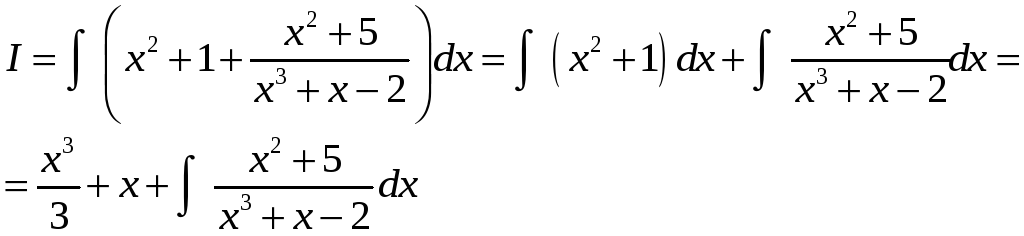Дробь, стоящую в последнем интеграле, разложим на простейшие: ,

Откуда

и .

Подставляя в первое равенство , получим или . Из второго равенства получаем систему

,

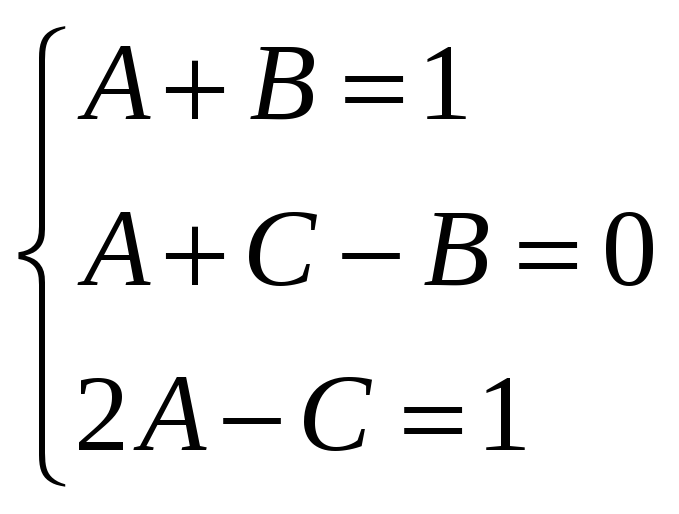из которой окончательно находим все коэффициенты: .

Вернемся к интегралу от правильной дроби:

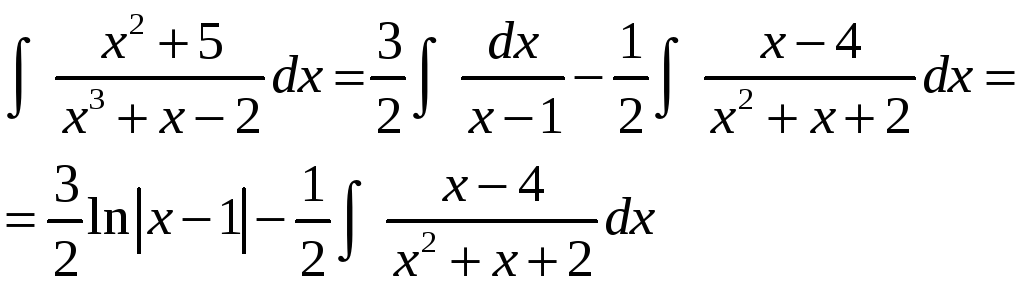
В последнем интеграле выделим полный квадрат в знаменателе 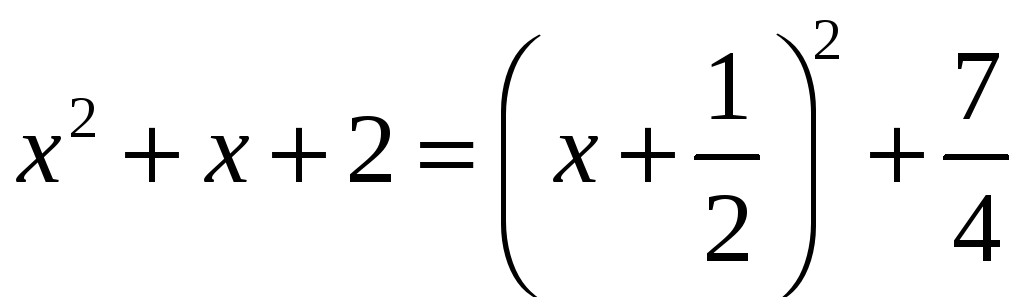и сделаем замену переменной . Тогда 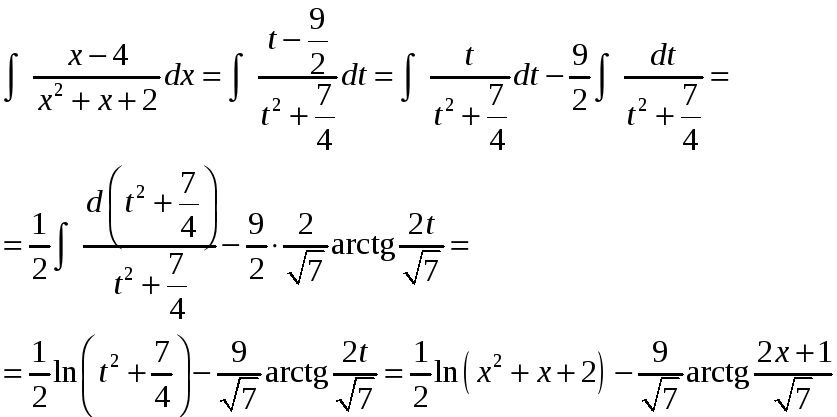. Окончательно,

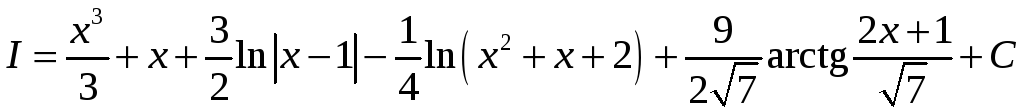
В задании IV требуется проинтегрировать некоторую тригонометрическую функцию. Рассмотрим основные приемы вычисления подобных интегралов.

1. Интеграл вида , где - рациональная функция, можно привести к интегралу от рациональной дроби универсальной тригонометрической подстановкой . Используя формулы тригонометрии, получим 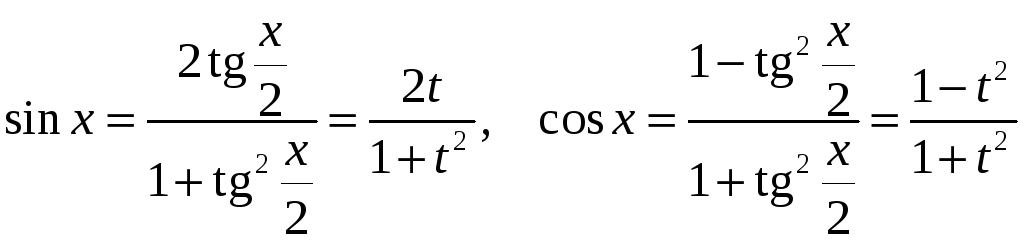. Кроме того , откуда .

Применение этой подстановки доказывает, что каждый интеграл сводится к интегралу от рациональной функции и, следовательно, первообразная функции , стоящей под интегралом, выражается через элементарные функции.

2. Универсальная тригонометрическая подстановка очень часто приводит к дроби, интегрирование которой представляет собой весьма трудоемкий процесс. Поэтому эта подстановка на практике используется очень редко. Чаще при вычислении интеграла вида , где - рациональная функция двух переменных, применяются следующие подстановки:

а) Если функция нечетна относительно первой переменной, т.е. , то применяется подстановка .

b) Если функция нечетна относительно второй переменной, т.е. , то применяется подстановка .

c) Если функция четна относительно обеих переменных, т.е. , то применяется подстановка .

3. Интегралы вида , и приводятся к табличным с помощью формул преобразования произведения тригонометрических функций в сумму.

4. Рассмотрим интегралы вида , где n и m – целые неотрицательные числа.

Если n – нечетное число, то можно сделать подстановку . Тогда , и данный интеграл приводится к виду . Если n – число четное, но нечетным будет m, то аналогично можно сделать подстановку и привести интеграл к виду .

Если оба показателя n и m четные, то применяют формулы понижения степени: .

5. Некоторые интегралы от рациональных и иррациональных функций легко вычисляются с помощью тригонометрических подстановок, в частности:

• интеграл вида 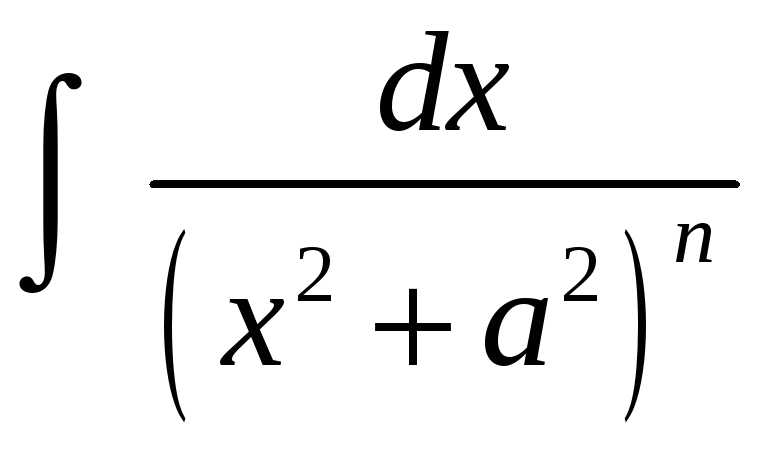можно вычислить с помощью подстановки ;

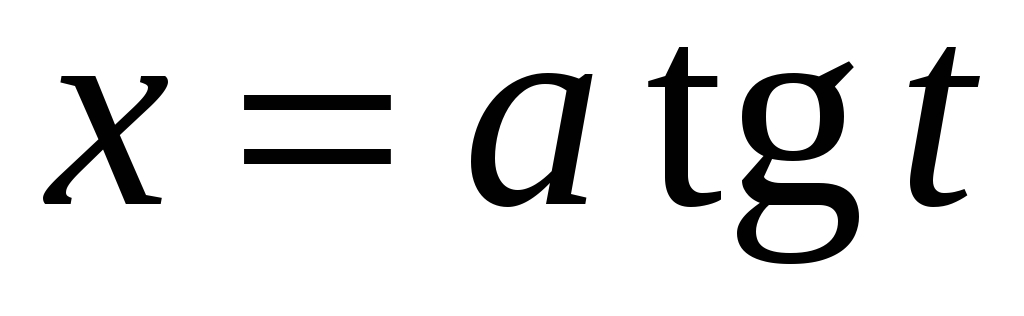• интеграл вида можно вычислить с помощью подстановки ;

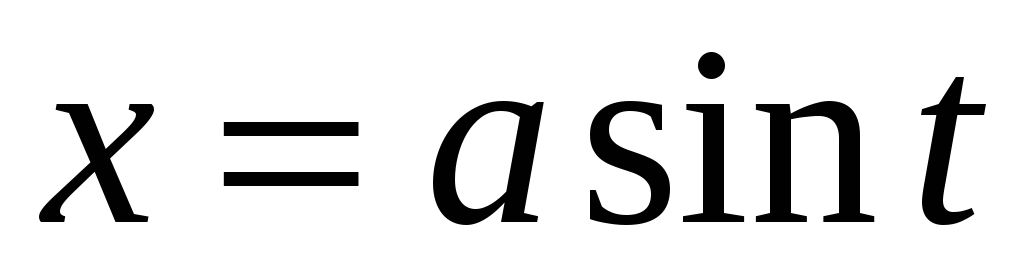• интеграл вида 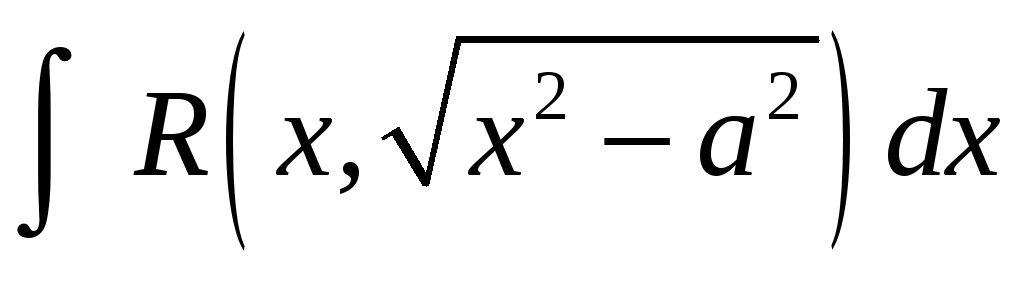можно вычислить с помощью подстановки ;

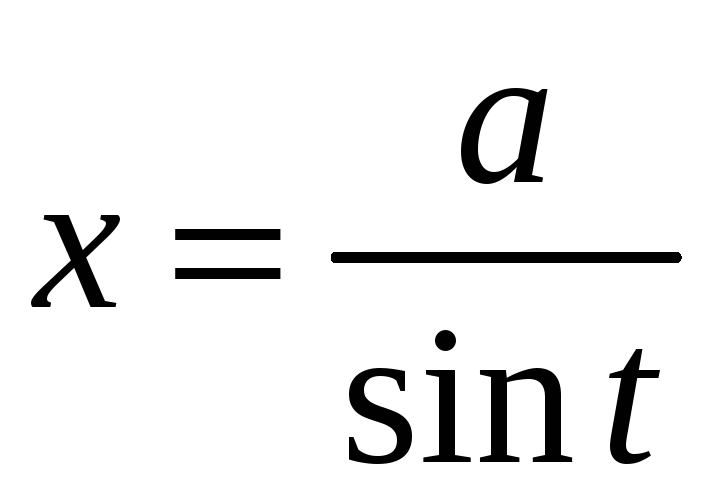• интеграл вида 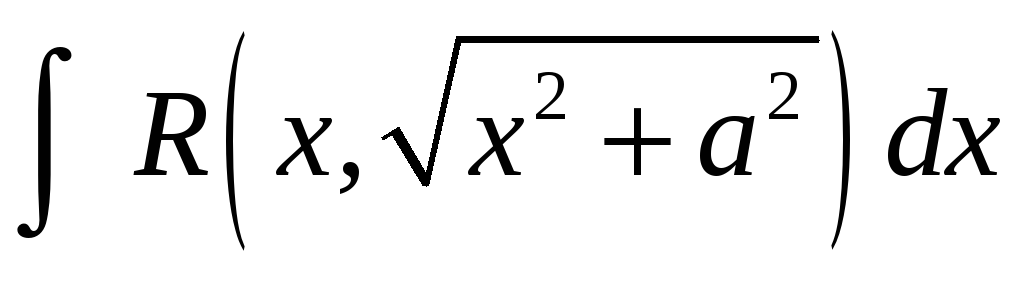можно вычислить с помощью подстановки .

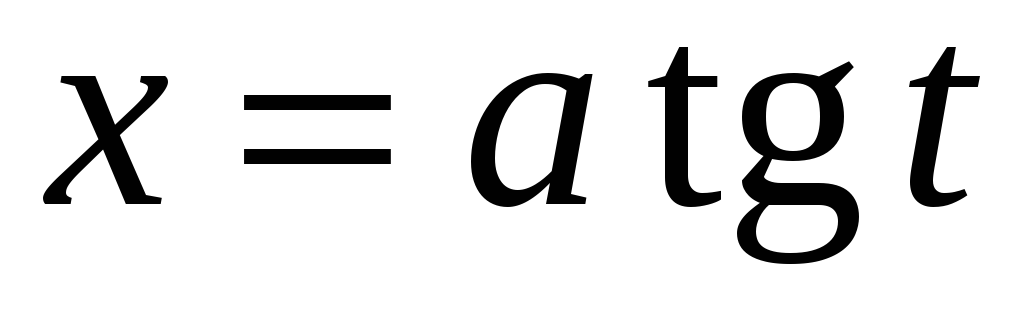Рассмотрим несколько примеров.

Пример 6. Найти интеграл .

Решение. Применим универсальную тригонометрическую подстановку*: .

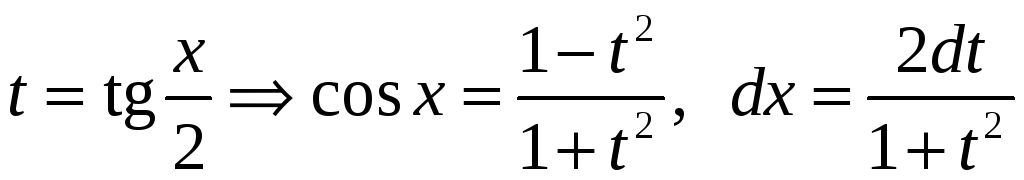Тогда

.

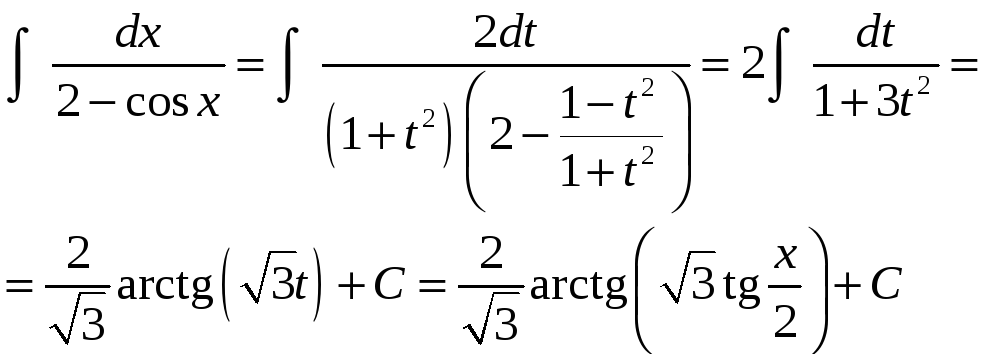Пример 7. Найти интеграл .

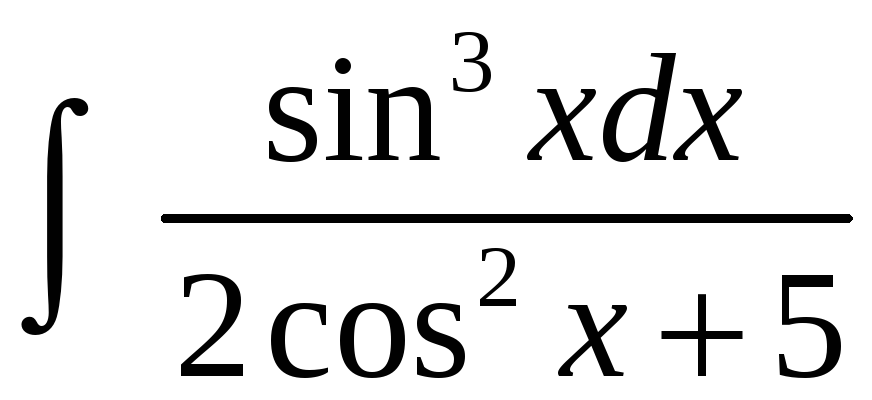Решение. Функция, стоящая под интегралом, нечетна относительно синуса: 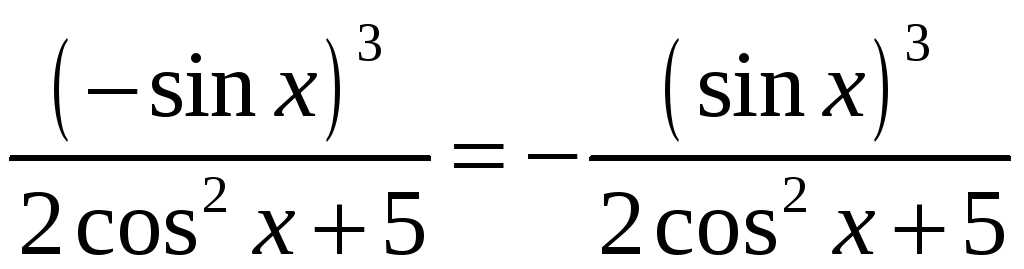, поэтому сделаем подстановку . Тогда

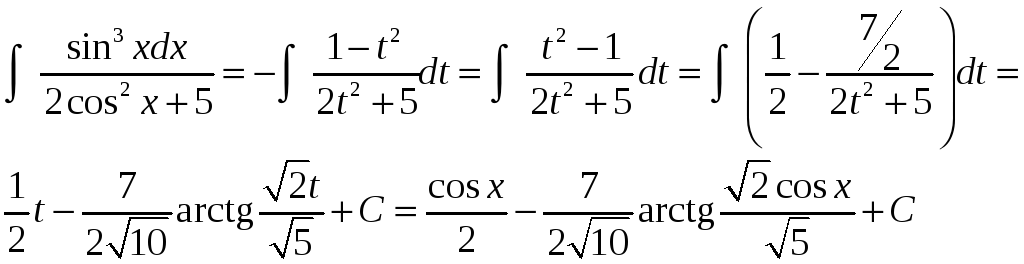
Пример 8. Найти интеграл .

Решение. Преобразуем произведение, стоящее под знаком интеграла в сумму:

.

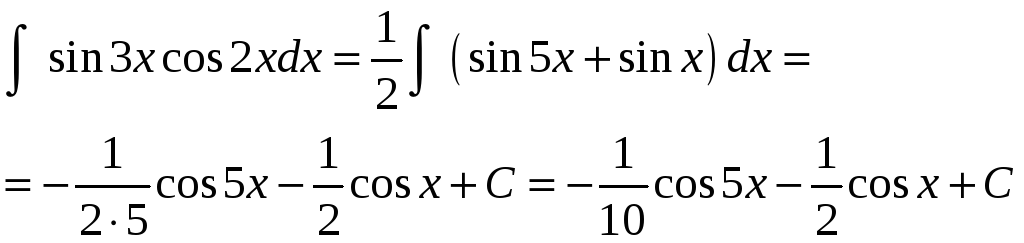Пример 9. Найти интеграл .

Решение. Так как стоит в нечетной степени, то сделаем замену . Тогда

.

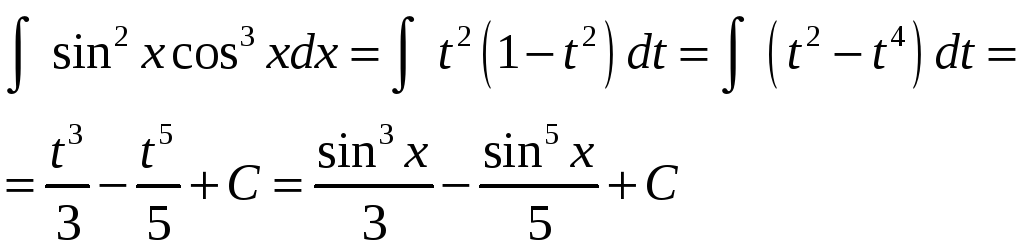Пример 10. Вычислить интеграл .

Решение. Здесь стоит в четной степени, поэтому воспользуемся формулами понижения степени:

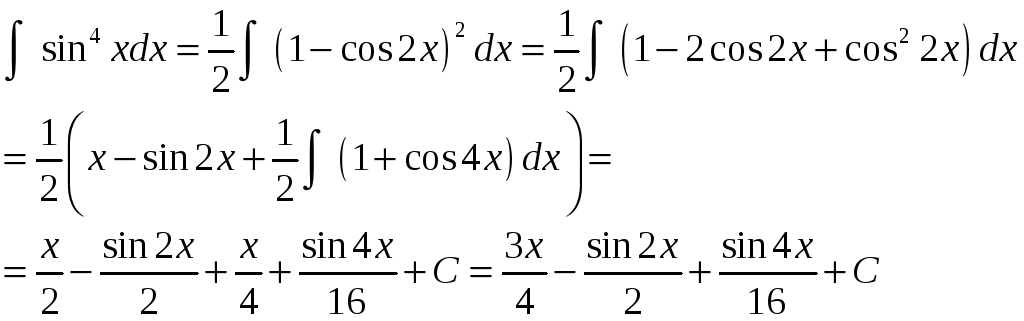
В задании V требуется найти площадь плоской фигуры с использованием определенного интеграла. Приведем основные формулы, необходимые для этого.

Если область ограничена сверху кривой , снизу кривой , причём , то площадь области можно вычислить по формуле

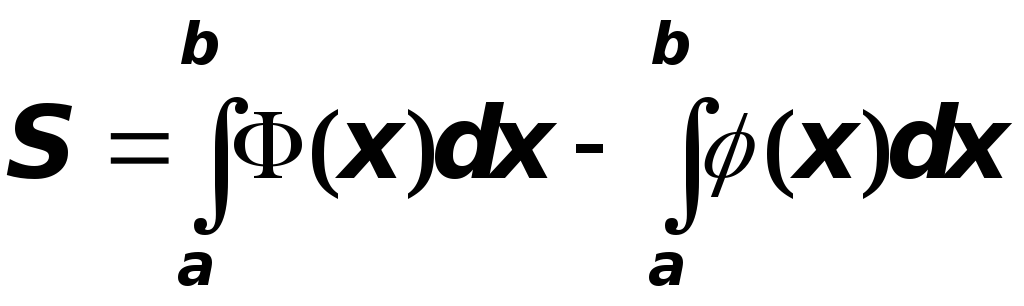, т.е.

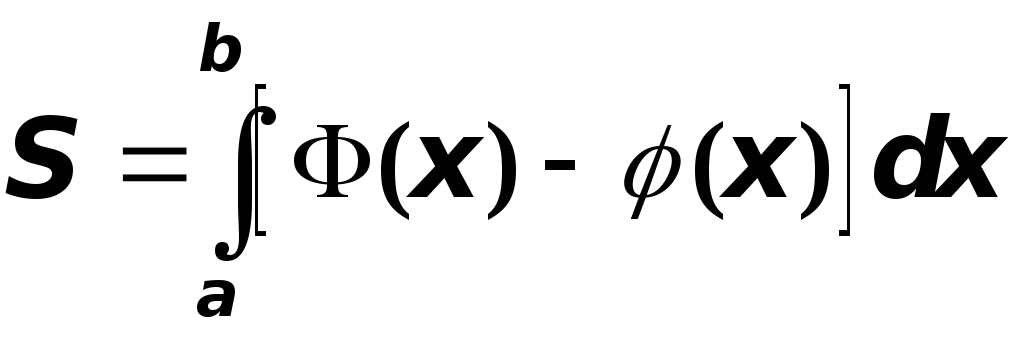
Если кривая задана параметрически 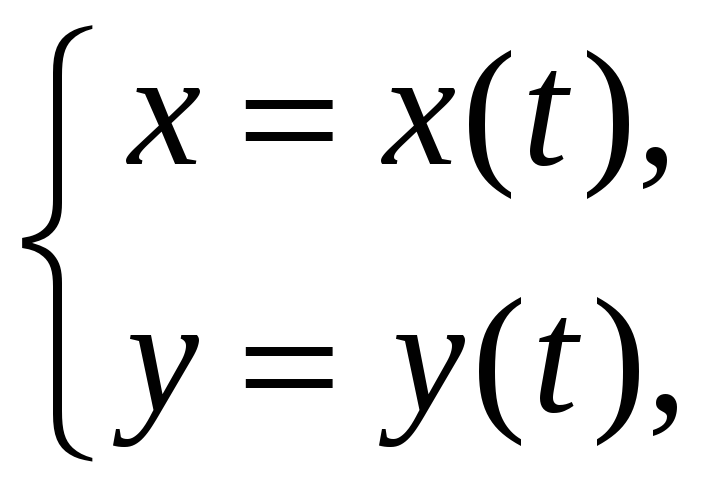и при изменении параметра точка пробегает кривую L , лежащую выше оси OX от до, то площадь криволинейной трапеции, ограниченной данной кривой, осью абсцисс и прямыми и находится по формуле 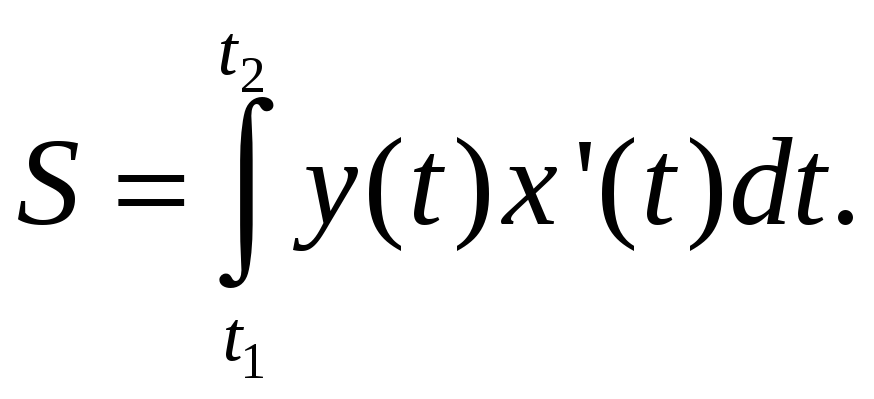По той же формуле можно найти и площадь фигуры, ограниченной замкнутой кривой L , заданной параметрически и пробегаемой по часовой стрелке,. При этом соответствуют значениям параметра, при которых кривая замыкается.

Пример 11. Вычислить площадь фигуры, ограниченной кривыми и .

Решение.

Найдём точки пересечения данных кривых. Для этого необходимо решить систему уравнений

Р

ешив её, найдём координаты точек и . Тогда, очевидно, что площадь фигуры

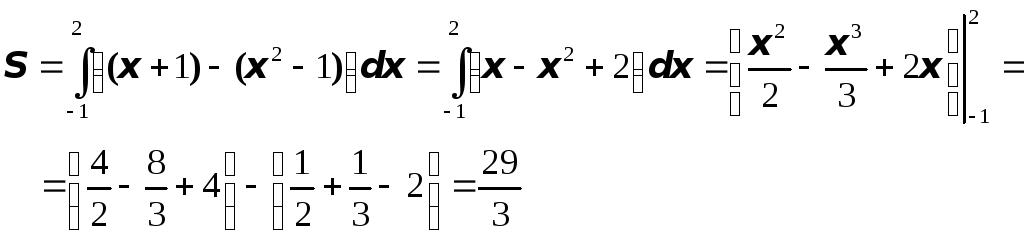
Кривая, ограничивающая область, может быть задана в полярных координатах. Точнее, рассмотрим площадь фигуры, ограниченной лучами , а также кривой (предполагаем, естественно, что функция на промежутке интегрируема). Площадь данного криволинейного сектора находится по формуле .

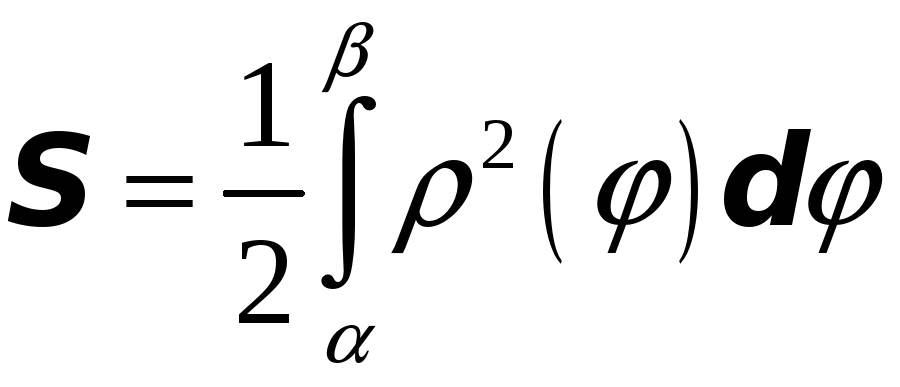В задании VI требуется вычислить длины кривых, заданных тремя различными способами.

Если кривая задана в прямоугольной системе координат, уравнением , где , то ее длина находится по формуле

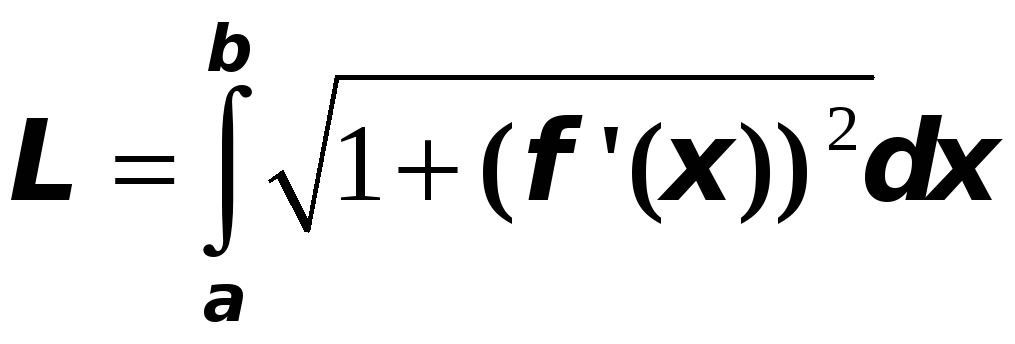
Если кривая задана параметрическими уравнениями

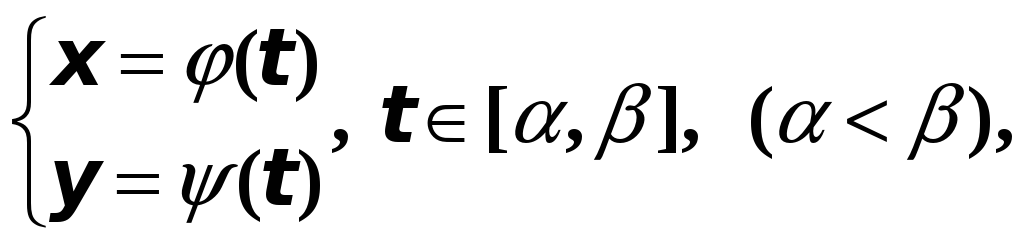
то длина дуги кривой вычисляется по формуле

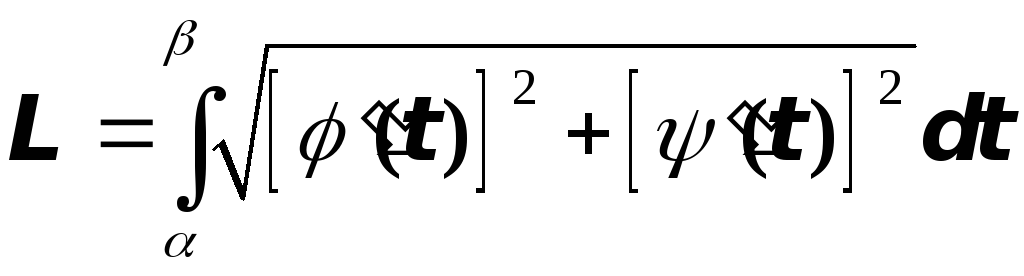
Отметим, что здесь, естественно, предполагается, что функции , и их производные и непрерывны на промежутке .

В том случае, когда кривая задана уравнением в полярных координатах , причём функция и её производная непрерывны на промежутке , то

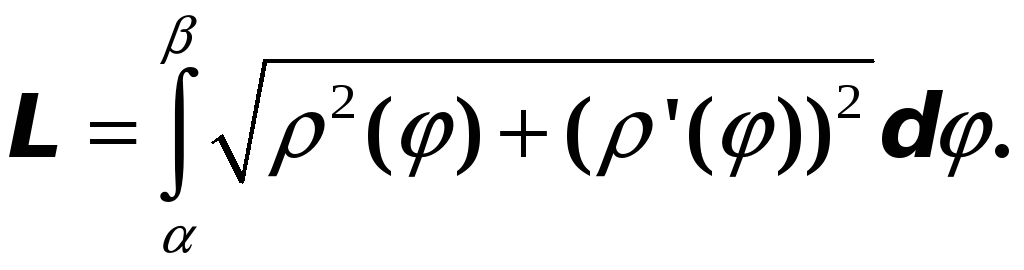
Пример 12. Найти длину дуги кривой

Решение.

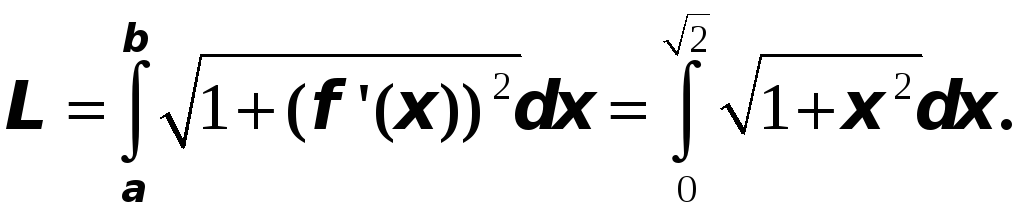
Найдем сначала неопределенный интеграл. Сделаем замену переменной (подстановка Эйлера):

(*)

Выразим x через t.

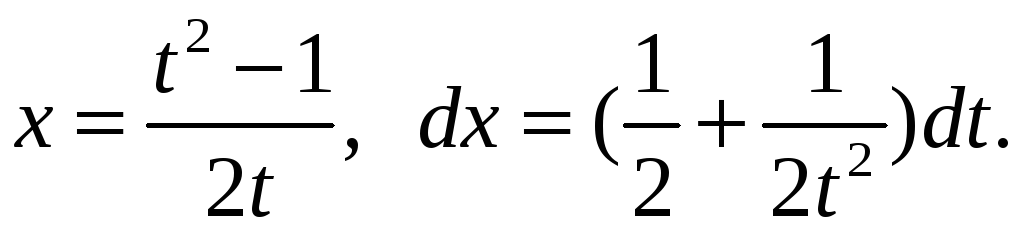
Подставляем в интеграл, учитывая выражение (*) для корня.

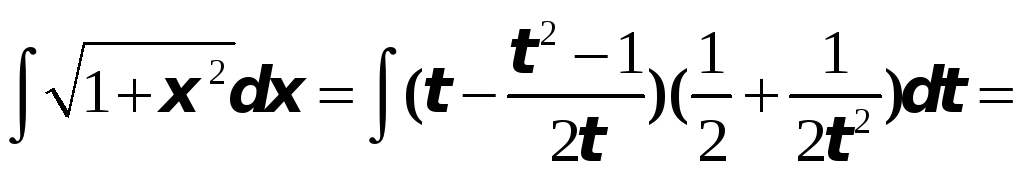
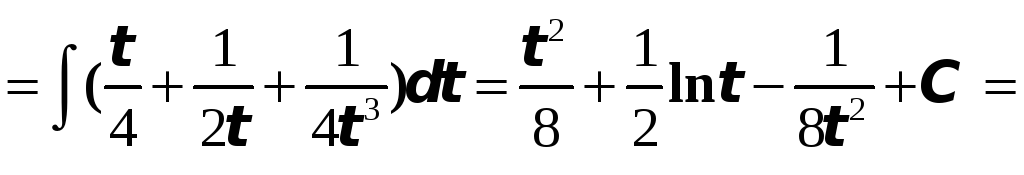
Теперь по формуле Ньютона-Лейбница получаем результат:

В задании VII требуется вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций. Причем функция может быть задана в декартовых, параметрических или полярных координатах.

Если объем V тела существует и есть площадь сечения тела плоскостью, перпендикулярной к оси Ох в точке x, то

.

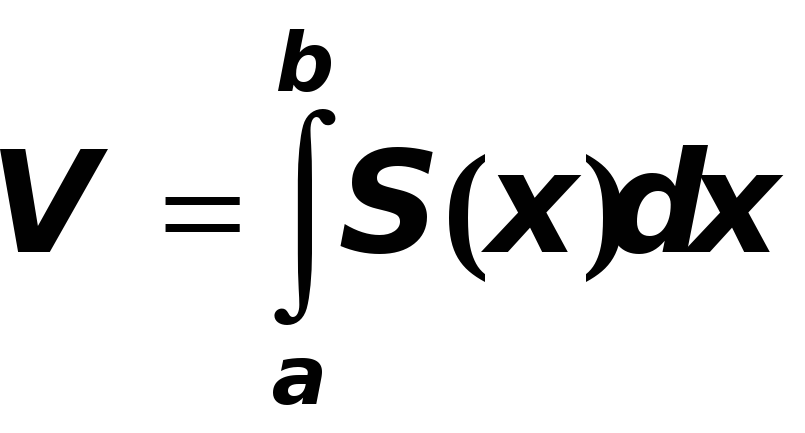Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции , где - непрерывная однозначная функция, равен

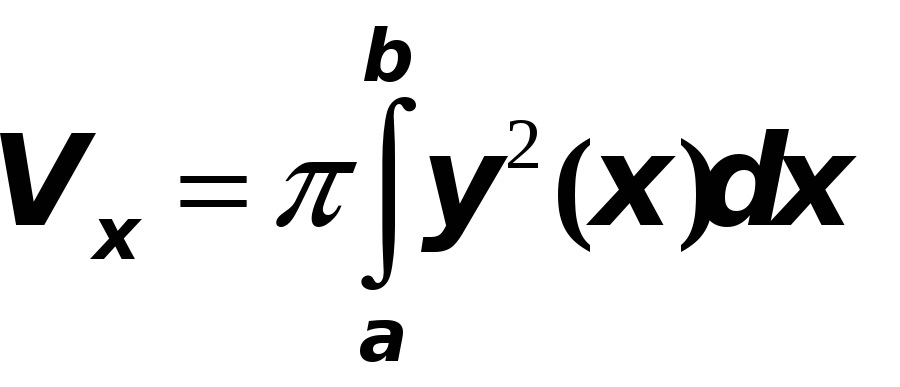
Если криволинейная трапеция, ограниченная кривой , , вращается вокруг оси Оу, то объем тела вращения вычисляется по формуле:

.

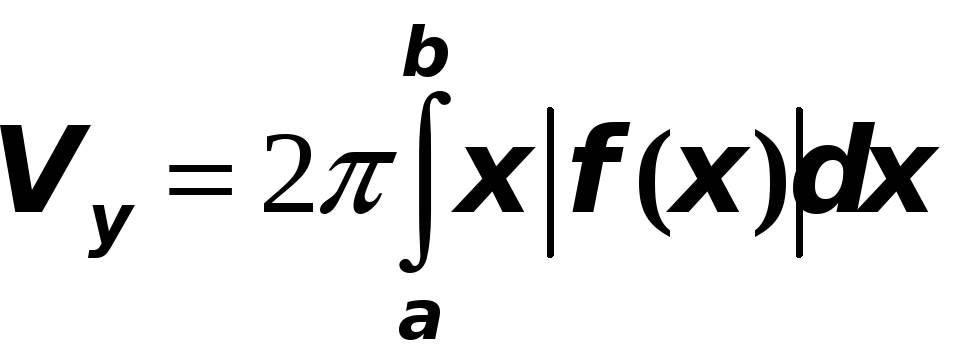Если криволинейный сектор, ограниченный кривой и лучами вращается вокруг полярной оси, то объем тела вращения равен:

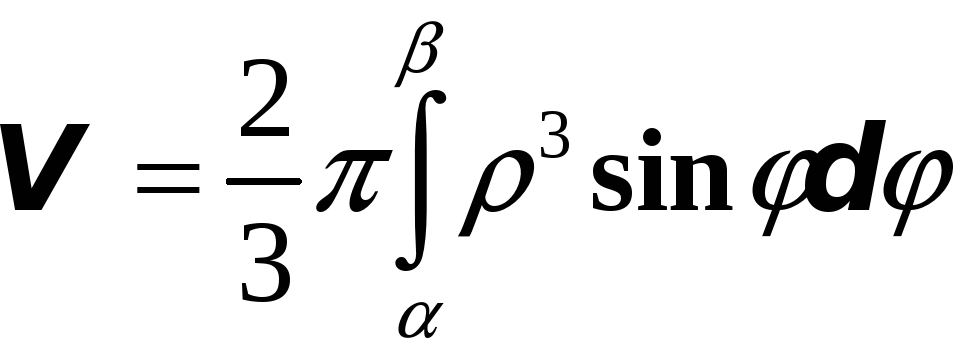
Рассмотрим типовые задачи:

Пример 13. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями и .

Решение. Т.к. область значений функции - , то фигура, ограниченная заданными линиями будет лежать в верхней полуплоскости.

Найдём абсциссы точек пересечения кривых. Для этого решим систему уравнений:

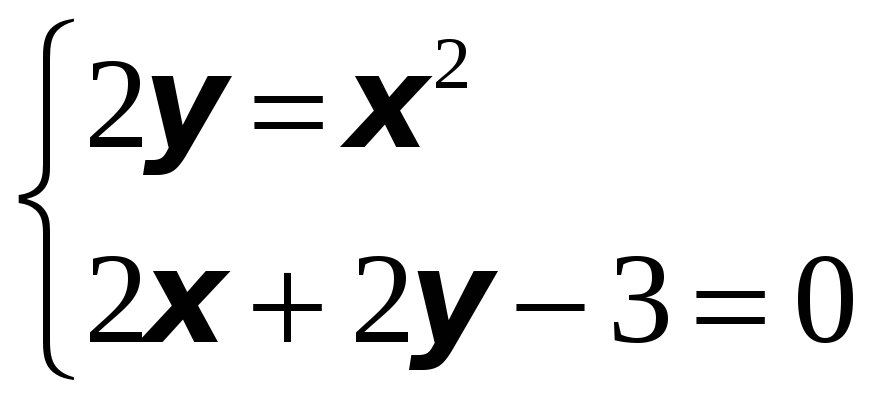
Имеем , .

Тогда, объем тела:

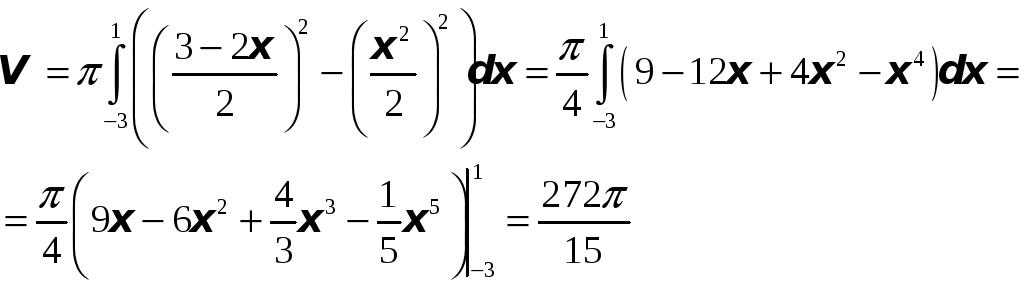
Пример 14. Фигура, ограниченная кривой , и осью Ox, вращается вокруг оси Оy. Найти объем тела вращения.

Решение. Если t=0, то x=4, y=0, если t=, то x=0, y=0. Причем и . Следовательно, объем тела вращения равен:

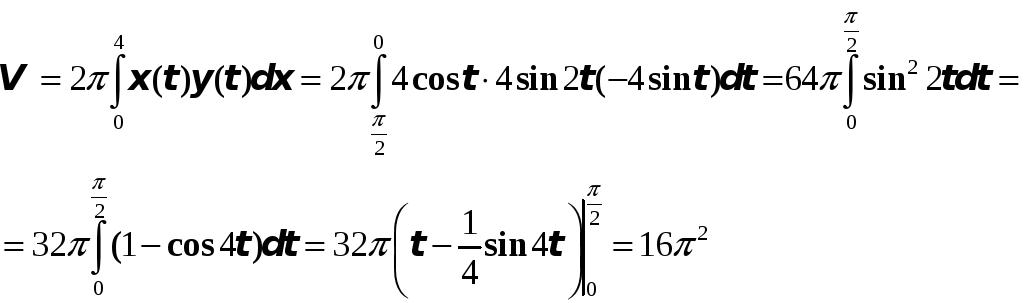
Пример 15. Фигура, ограниченная линией , вращается вокруг полярной оси. Найти объем тела вращения.

Решение. Фигура симметрична относительно полярной оси, поэтому для вычисления объема достаточно вращать ее верхнюю половину .