
- •I. Пределы
- •1.1. Понятие о пределе числовой последовательности.
- •1.2.Правила вычисления пределов последовательностей.
- •1.3. Число е.
- •1.4. Предел функции.
- •1.5. Правила вычисления пределов функции.
- •Раскрытие неопределенностей вида и .
- •1.7. Раскрытие неопределенности вида .
- •1.8. Два замечательных предела.
- •1.9. Сравнение бесконечно малых.
- •II. Дифференцирование.
- •Понятие производной.
- •Вычисление производных.
- •Дифференциал функции.
- •Производные и дифференциалы высших порядков.
- •2.5. Производная неявной функции и параметрически заданной функции.
- •Исследование функций и построение графиков.
- •Основные положения исследования функции.
- •Глава 1.
- •Глава 2.
- •Глава 3.
Глава 1.
-
1)
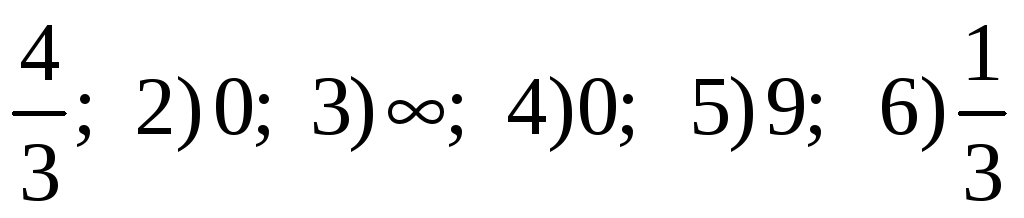 ;
7)
;
7)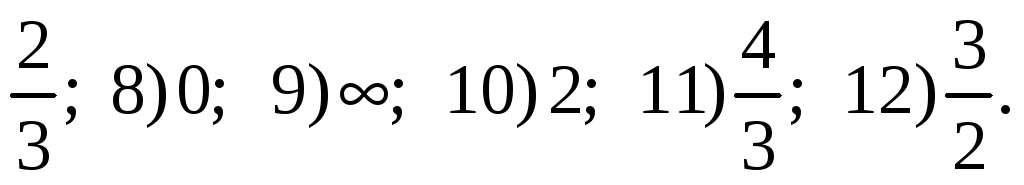
-
1)
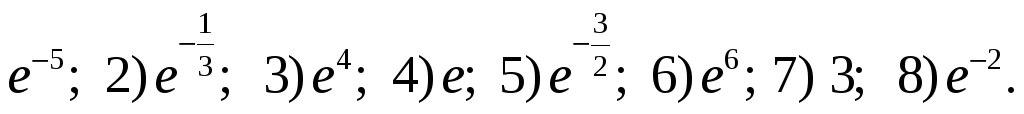
-
1)
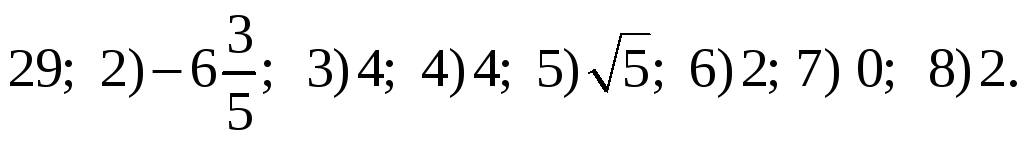
-
1)
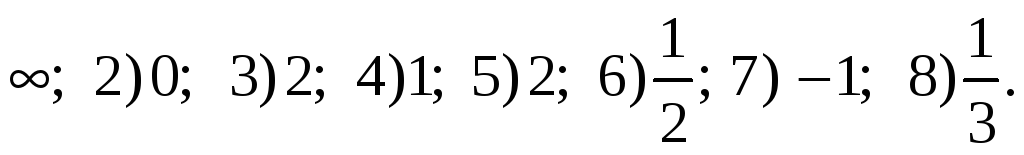
-
1)
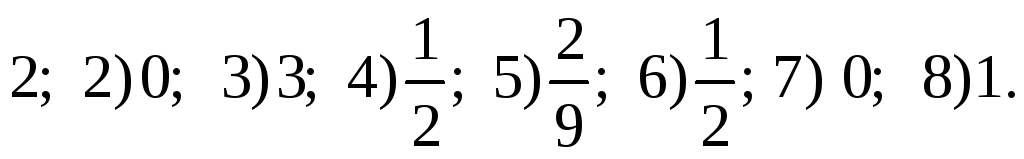
-
1)
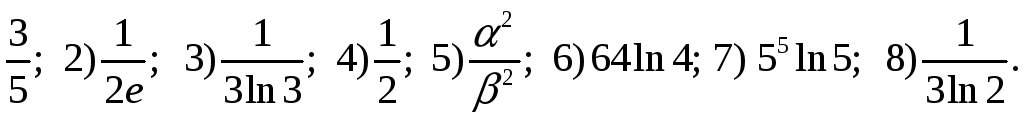
Глава 2.
2.1. 1)
![]()
2.2.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()

![]()
![]()

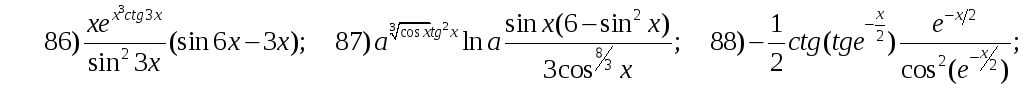

![]()
2.3.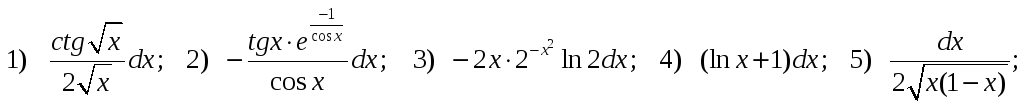
![]()
![]()

14) 10,05; 1,02;
6,41; 2,08; 2,01; 15) 1,15; 1,072;
![]() .
.
2.4.
![]()
![]()
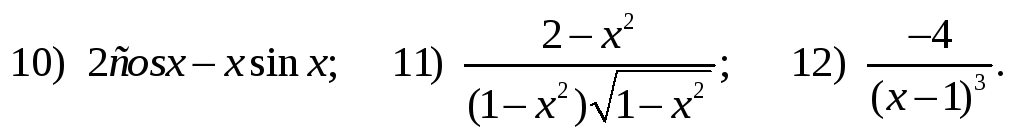
2.5.
![]()
![]()
2.6.
![]()
5)
![]() ;
;
![]()
![]()
![]()
2.7.
![]()
![]()
2.8. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
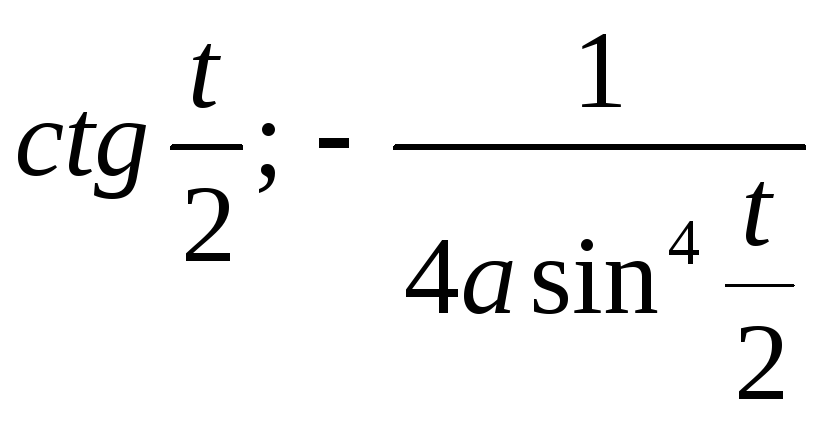 ; 4)
; 4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
.
Глава 3.
3.1. 1)
При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;
2) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;
3) Область определения
функции
![]() .
При
.
При
![]() - максимум,
- максимум,
![]() ,
при
,
при
![]() выпуклость вверх;
выпуклость вверх;
4) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;
![]() -
горизонтальная асимптота при
-
горизонтальная асимптота при
![]() ;
;
5) Область определения
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
6) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
;
7) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - точка перегиба,
- точка перегиба,
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
8) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;
9) Экстремальных
точек нет;
![]() - вертикальные асимптоты,
- вертикальные асимптоты,
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
10) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() ,
,
![]() - точки перегиба;
- точки перегиба;
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
11) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;
![]() - вертикальная асимптота,
- вертикальная асимптота,
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
12) При
![]() - максимум,
- максимум,
![]() ;
;
![]() - вертикальные асимптоты;
- вертикальные асимптоты;
![]() - горизонтальная асимптота;
- горизонтальная асимптота;
13) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - точка перегиба;
- точка перегиба;![]() - горизонтальная асимптота при
- горизонтальная асимптота при
![]() ;
;
14) При
![]() - минимум,
- минимум,
![]() ;
точек перегиба нет;
;
точек перегиба нет;
![]() - вертикальная асимптота при
- вертикальная асимптота при![]() ;
;
15) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - точки перегиба;
- точки перегиба;
![]() -
горизонтальная асимптота;
-
горизонтальная асимптота;
16) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - точки перегиба;
- точки перегиба;![]() - горизонтальная асимптота при
- горизонтальная асимптота при
![]() ;
;
17) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
;
![]() - вертикальные асимптоты;
- вертикальные асимптоты;
![]() -
горизонтальная асимптота при
-
горизонтальная асимптота при
![]() ;
;
18) Экстремальных
точек нет. При
![]() - точки перегиба;
- точки перегиба;
![]() - горизонтальные асимптоты;
- горизонтальные асимптоты;![]() ;
;
19) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
;![]() - горизонтальная асимптота; функция
неотрицательная.
- горизонтальная асимптота; функция
неотрицательная.
20) При
![]() - минимум,
- минимум,
![]() ;
функция положительная ;
;
функция положительная ;
![]() - вертикальная асимптота при
- вертикальная асимптота при
![]() ;
;
21) При
![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() - максимум,
- максимум,
![]() ;
;![]() - наклонная асимптота;
- наклонная асимптота;
![]() - вертикальная асимптота;
- вертикальная асимптота;
22) При
![]() - максимум,
- максимум,
![]() ;
при
;
при
![]() -
максимум,
-
максимум,
![]() ;
при
;
при
![]() - минимум,
- минимум,
![]() ;
;![]() - наклонная асимптота;
- наклонная асимптота;
![]() - вертикальная асимптота; при
- вертикальная асимптота; при
![]() -
точка перегиба;
-
точка перегиба;
23) При
![]() - минимум,
- минимум,
![]() ;
точек перегиба нет;
;
точек перегиба нет;
![]() - наклонная асимптота;
- наклонная асимптота;
![]() - вертикальная асимптота;
- вертикальная асимптота;
24) При
![]() - минимум,
- минимум,
![]() ;
;
![]() - наклонная асимптота при
- наклонная асимптота при
![]() ;
;
![]() - вертикальная асимптота при
- вертикальная асимптота при
![]() ;
;
25) При![]() - минимум,
- минимум,
![]() ;
при
;
при
![]() -
максимум,
-
максимум,
![]()
![]() - вертикальная асимптота,
- вертикальная асимптота,
![]() -
наклонная асимптота;
-
наклонная асимптота;
26) При
![]() - минимум, y
=
- минимум, y
=![]() ;
(1;0) - точка пересечения с осью Ох;
;
(1;0) - точка пересечения с осью Ох;
![]() ,
точек перегиба нет;
,
точек перегиба нет;
27) Экстремальных
точек нет. При х = 0 – точка перегиба;
![]() - наклонная асимптота при
- наклонная асимптота при
![]() ,
,
![]() - наклонная асимптота при
- наклонная асимптота при
![]() .
.
Литература
-
Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: ООО «Издательство АСТ», 2002.
-
Кузнецов Л.А. Сборник задач по высшей математике. Типовые расчёты. СПб.: Издательство «Лань», 2005.
-
Вельмисова С.Л., Червон С.В. Математический анализ, часть 1. Ульяновск: УлГУ, 2009.
