1.7. Раскрытие неопределенности вида .
Неопределенность
вида
при помощи
алгебраических преобразований
приводится
к неопределенности
.
Пример 1.15.
Найти
.
Решение.
Имеем
неопределенность вида
.
Умножим и разделим рассматриваемое
выражение на сопряженное и заменим
знаменатель на эквивалентную величину:
=
.
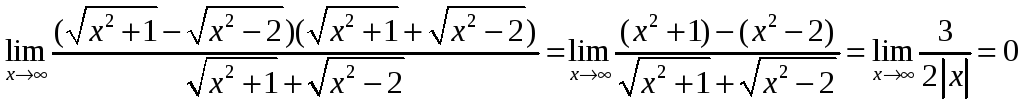J
Пример 1.16.
Найти
.
Решение.
Имеем
неопределенность вида
.
Для вычисления
этого предела используем прием умножения
и деления на сопряженное выражение:
=
=
=
=
.
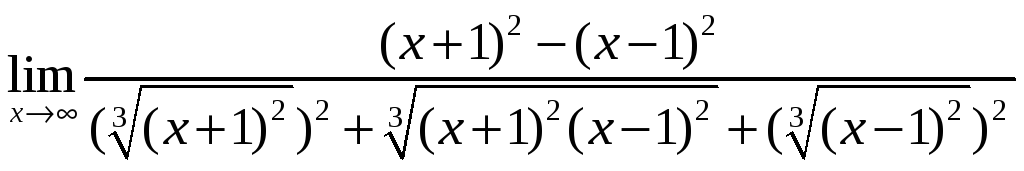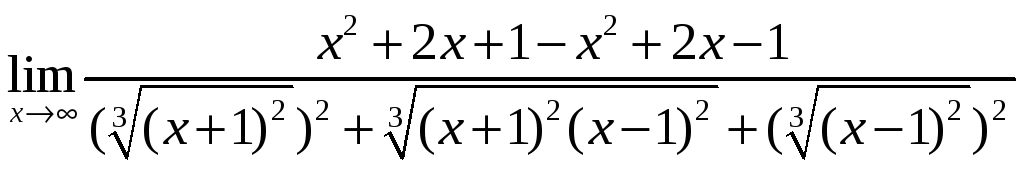J
Пример 1.17.
Найти
.
Решение.
Имеем
неопределенность вида
.
Преобразуем
данное
выражение и найдем предел дроби:
=
=
=
=
.
J
☼ Упражнения 1.6. Найти пределы:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.
☼
1.8. Два замечательных предела.
Рассмотрим два предела, имеющих важное значение.
Первый
замечательный предел:
.
Пример 1.18.
Найти
.
Решение.
.
J
Пример 1.19.
Найти
.
Решение.
.
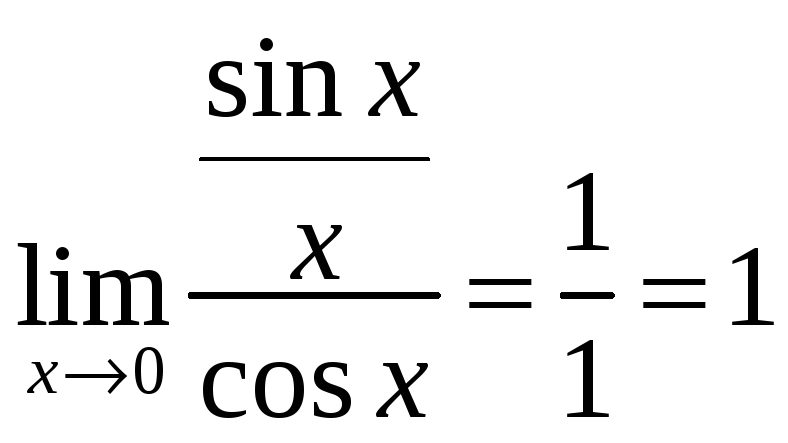J
Пример 1.20.
Найти
.
Решение.
Положим
.
Тогда
.
Заметим, что
при
.
Имеем:
.
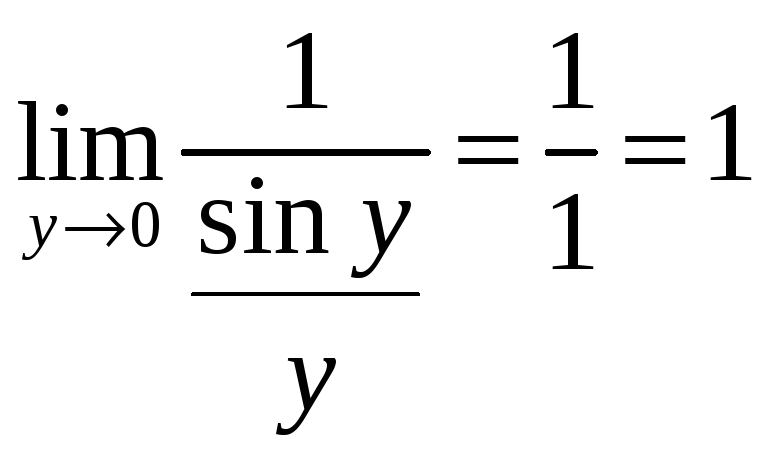J
Аналогичным
образом, принимая во внимание, что
,
можно установить, что
.
Пример 1.21.
Найти
.
Решение.
.
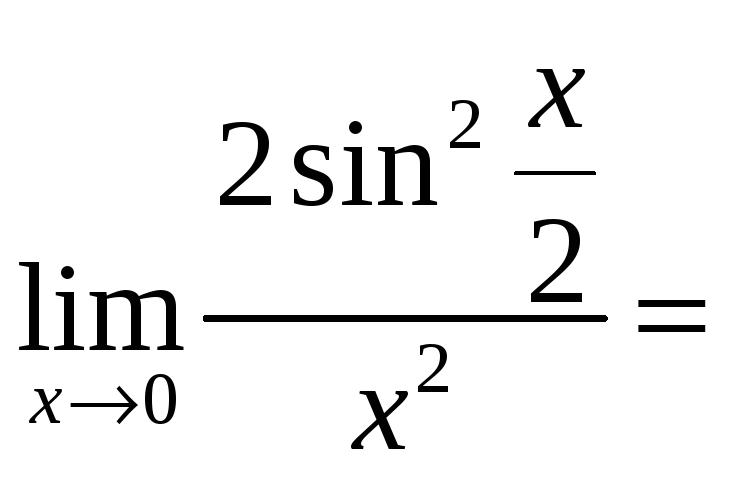
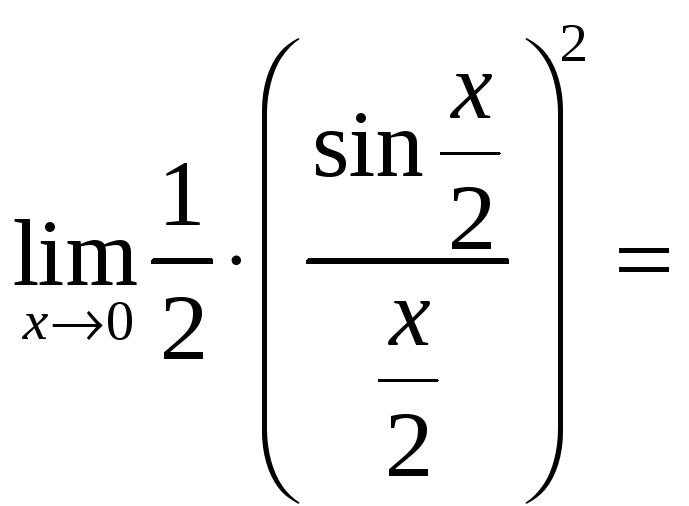
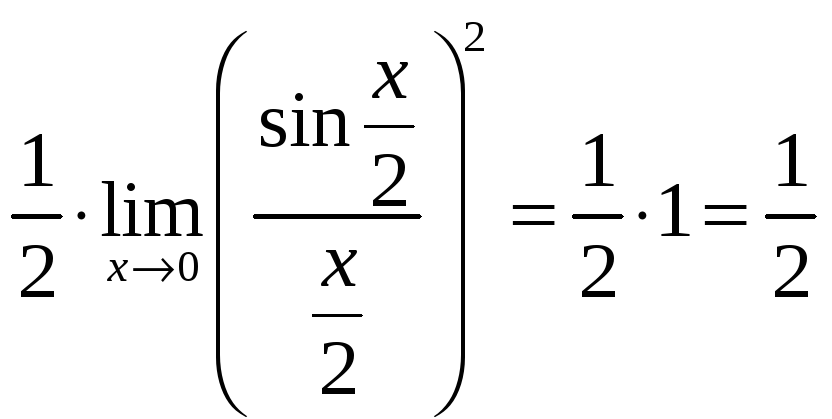J
Второй
замечательный предел:
.
Пример 1.22.
Найти
.
Решение.
.
J
Пример 1.23.
Найти
.
Решение.
Положим
.
Тогда
.
Заметим, что
при
.
.
J
Полученное соотношение является частным случаем предела
,
для получения
которого использовались преобразования:
.
1.9. Сравнение бесконечно малых.
Функция
называется
бесконечно
малой при
,
если
.
Пусть
и
- две бесконечно малые функции при
.
Тогда:
-
если
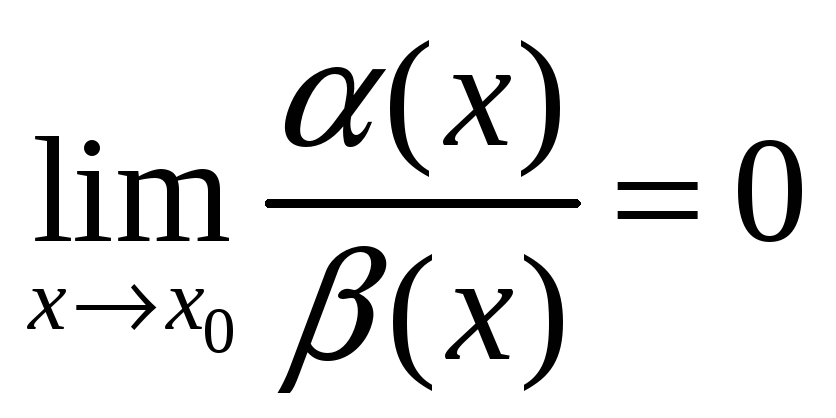, то
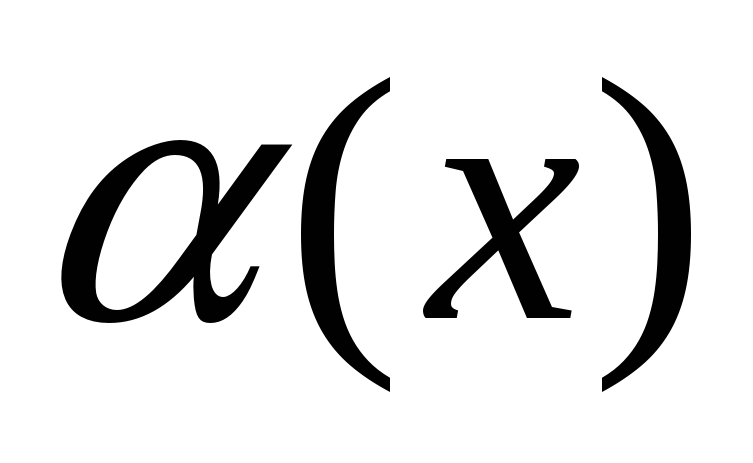называется бесконечно
малой более высокого порядка, чем
;
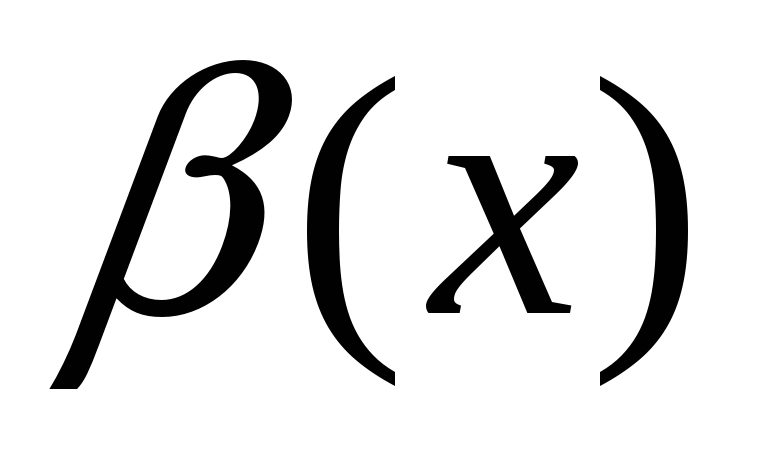2) если
,
то
и
называются
бесконечно малыми одного порядка;
3)
если
,
то
и
называются эквивалентными
бесконечно малыми, обозначение
:
;
4)
если
, то
называется
бесконечно малой n-го
порядка относительно
;
Пример 1.24.
Доказать,
что при
функции
и
- эквивалентные бесконечно малые (
при
).
Решение.
Действительно,
.
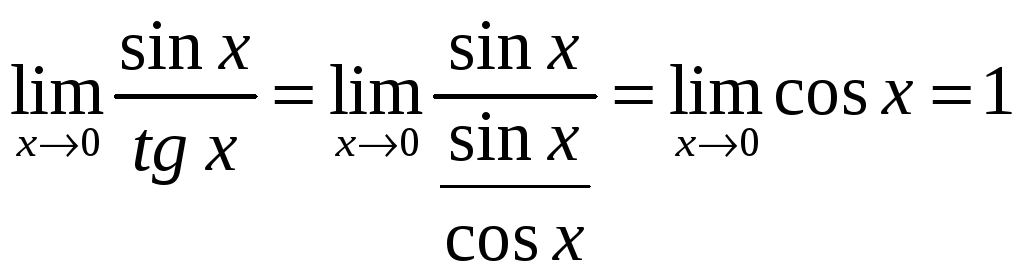J
Результаты решения примеров 1.19 - 1.23 являются следствиями из 1-го и 2-го замечательных пределов. Запишем эти следствия и некоторые другие, получающиеся подобным образом,
в виде таблицы
эквивалентных бесконечно малых. При
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.25.
Найти
.
Решение.
При
и
и, значит,
,
.
Заменяя числитель и знаменатель на
эквивалентные бесконечно малые, получаем
.
Пример 1.26.
Найти
.
Решение.
.
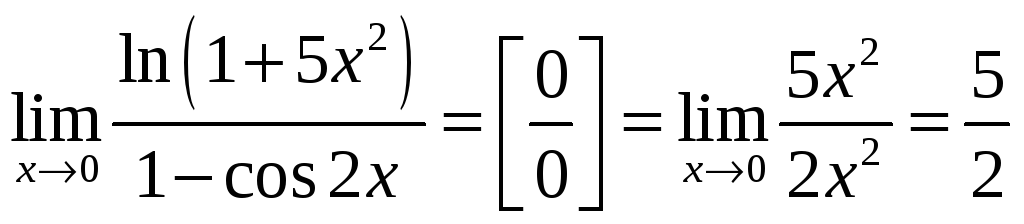Пример 1.27.
Найти
.
Решение.
=
=
.
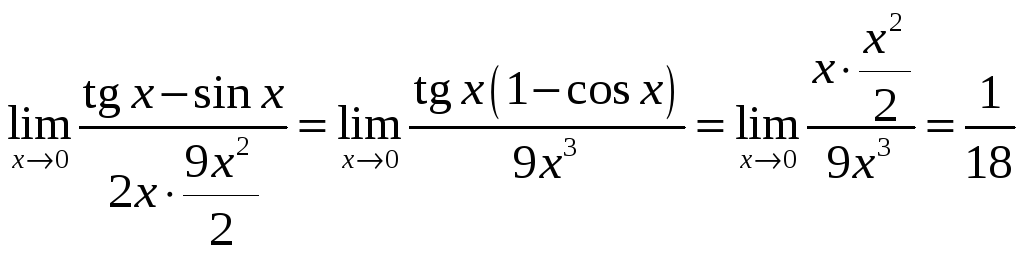Пример 1.28.
Найти
.
Решение.
.
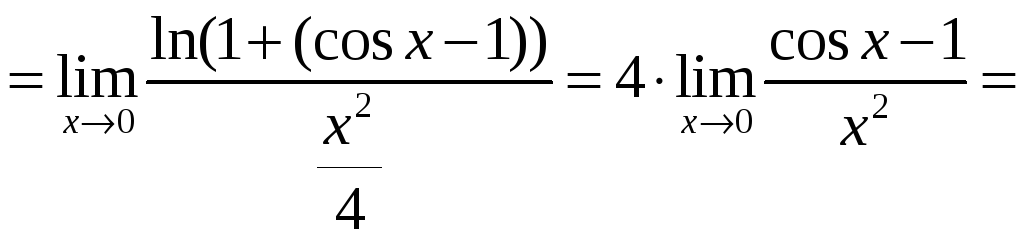
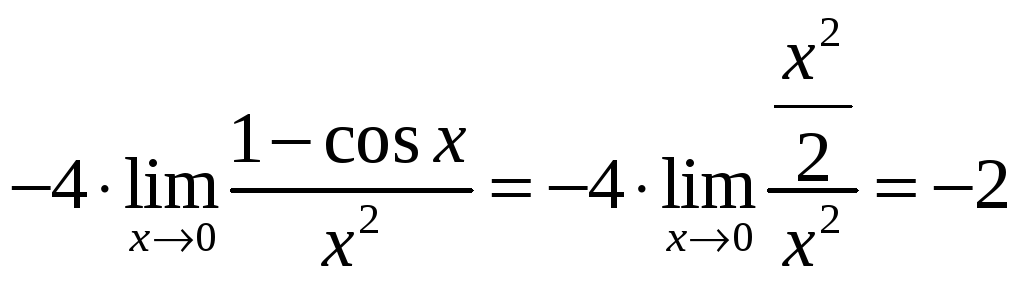- Мой дорогой Уотсон, попробуйте немного
проанализировать сами, - сказал он с легким
раздражением.- Вы знаете мой метод. При-
мените его, и будет поучительно сравнить
результаты.
А.Л. Дойл. Знак четырех.
☼ Упражнения 1.7. Найти пределы:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
; 7)
; 8)
;
☼