3. Гипербола

Гиперболой называется геометрическое место точек, модуль разности расстояний от каждой из которых до двух точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Систему координат выбираем так же, как и для эллипса. По определению r₁ – r₂= 2a, где и – фокальные радиусы точки М. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c. Выберем на гиперболе произвольную точку М(х, у). Тогда:

,

,

,

Обозначим с² – а² = b² (геометрически эта величина – меньшая полуось), тогда :

(3)

Получили каноническое уравнение гиперболы.

Исследуем форму гиперболы по каноническому уравнению:

1) Так как уравнение (3) содержит слагаемые только с четными степенями координат х и у, то эллипс симметричен относительно осей Ох и Оу, а так же относительно начала координат.

Ось симметрии, на которой находятся фокусы гиперболы, называется фокальной осью. Точка пересечения осей симметрии – центром гиперболы.

Точки A₁(−a; 0), A₂(a; 0) пересечения гиперболы с осью Ох называются вершинами гиперболы, а

сама ось – действительной осью гиперболы.

Другая ось (Oy) не имеет с гиперболой общих точек и называется мнимой.

Отрезки A₁A₂ и B₁B₂ называются соответственно действительной и мнимой осями гиперболы; числа a = OA₁ = OA₂, b = OB₁ = OB₂ – действительной и мнимой полуосями гиперболы.

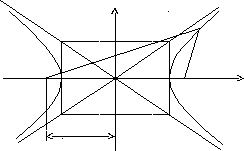y

M(x, y)

b

r₁

r₂

x

F₁ a F₂

c

2) Чтобы определить форму гиперболы, разрешим уравнение (3) относительно у: и, учитывая, что в I четверти , рассмотрим, в силу симметрии, уравнение :

• х = 0 гипербола не пересекает ось Оу;

• при возрастании х от 0 до а у – мнимые таких точек нет;

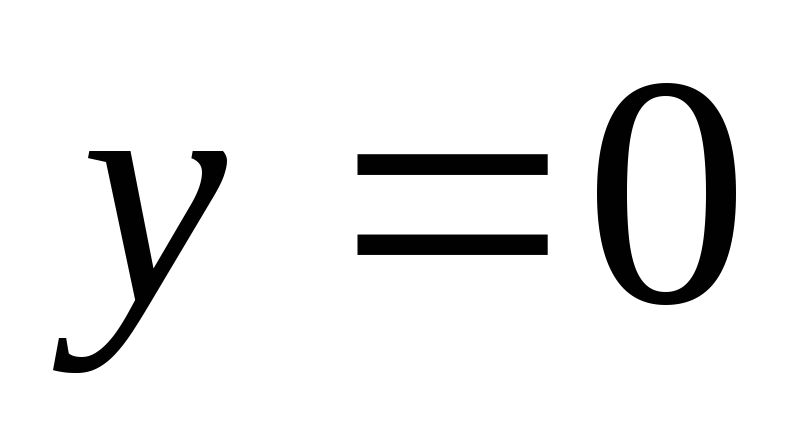
• х = а А(а; 0);

• при х > а у > 0. При возрастании х возрастает и у. Точка М на гиперболе перемещается с ростом х «вправо» и «вверх», причем её начальное положение – точка А(а; 0). Точка М, перемещаясь по гиперболе в бесконечность, неограниченно приближается к прямой 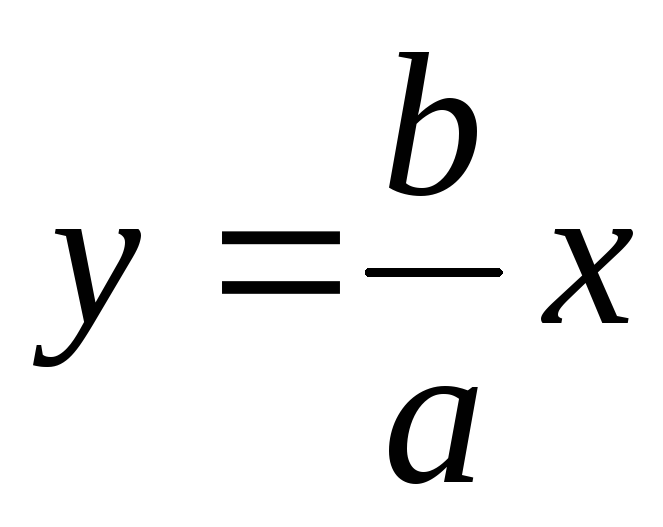, которая является асимптотой гиперболы (доказательство самостоятельно). Для её построения можно использовать прямоугольник.

Если в уравнении (3) переставить буквы местами, то получим уравнение сопряженной по отношению к (3) гиперболы:

Эти гиперболы имеют одни и те же асимптоты.

Замечание. Гипербола, полуоси которой равны a = b, называется равносторонней. Ее каноническое уравнение приводится к виду x² − y²= a². Асимптоты равносторонней гиперболы перпендикулярны.

Итак, частью гиперболы, расположенной в I четверти, является дуга АМ. Отображая ее относительно обеих координатных осей, получаем всю гиперболу.

Введем ещё одну величину, характеризующую форму гиперболы.

Эксцентриситетом гиперболы  называется отношение её фокального расстояния к длине действительной оси, т.е.. Так как с > а, то > 1.

Принимая во внимание, что , найдем чем меньше эксцентриситет, т.е, чем ближе он к 1, тем меньше b/а основной прямоугольник гиперболы более вытянут в направлении действительной оси. Таким образом, эксцентриситет характеризует форму гиперболы.

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии от него, называются директрисами гиперболы: и . Правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной.

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы: , .