7

КРИВЫЕ ВТОРОГО ПОРЯДКА

1. Окружность

Окружностью называется геометрическое место точек, расстояние от каждой из которых до данной точки, называемой центром, есть величина постоянная.

Пусть окружность имеет радиус r, а центр в точке С(a; b). Точка М(х, у) – произвольная точка окружности. Тогда, по определению, СМ = r. По формуле расстояния между двумя точками находим:

(x – a)² + (y – b)² = R² (1)

(1) – каноническое уравнение окружности. Раскроем скобки. Получим уравнение второй степени. Таким образом, окружность – линия второго порядка.

Запишем общее уравнение второй степени: Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0, в котором А, В, С не равны нулю одновременно. Сравним его с уравнением окружности. Очевидно, чтобы уравнение второго порядка было уравнением окружности необходимо, чтобы:

1) А = С; 2) В = 0.

Частный случай уравнения (1) – уравнение окружности с центром в начале координат: x² + y² = R^2..

2. Эллипс

Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Для вывода уравнения эллипса введем на плоскости прямоугольную систему координат так, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение эллипса в этой системе координат.

Пусть F₁ и F₂ – фокусы, М – произвольная точка эллипса. Расстояние между фокусами обозначим через 2с, сумму расстояний от точки М до фокусов через 2а.

По определению .

Обозначим через и расстояния от точки М до фокусов: . Числа и называются фокальными радиусами точки М. Из определения следует, что точка М лежит на данном эллипсе в том и только том случае, когда + = 2а.

Чтобы получить искомое уравнение эллипса, нужно выразить и через х и у. Так как F₁ и F₂  расположены на оси Ох симметрично относительно начала координат, то они имеют соответственно координаты (–с; 0) и (с; 0). Тогда ,

– искомое уравнение эллипса. Упростим его.

Изолируем один из корней и возведем обе части равенства в квадрат:

.

Введем в рассмотрение новую величину (по условию ). Получим: . Разделим на : (2)

(2) – каноническое уравнение эллипса. Можно показать, что любая точка, координаты которой удовлетворяют уравнению (2), принадлежит эллипсу и, наоборот (Шипачев, с 78).

Исследуем форму эллипса по каноническому уравнению:

1) Так как уравнение (2) содержит слагаемые только с четными степенями координат х и у, то эллипс симметричен относительно осей Ох и Оу, а так же относительно начала координат.

Ось симметрии, на которой находятся фокусы эллипса, называется фокальной или большей осью. Точка пересечения осей симметрии – центром эллипса.

Точки A₁(−a; 0), A₂(a; 0), B₁(0; −b), B₂(0; b) пересечения эллипса с осями координат называются вершинами эллипса. Отрезки A₁A₂ и B₁B₂ называются соответственно большой и малой осями эллипса; числа a = OA₁ = OA₂, b = OB₁ = OB₂ – большой и малой полуосями эллипса.

2) Чтобы определить форму эллипса, разрешим уравнение (2) относительно у: и, учитывая, что в I четверти , рассмотрим, в силу симметрии, уравнение :

• х = 0 В(0; b);

• при возрастании х от 0 до а у уменьшается;

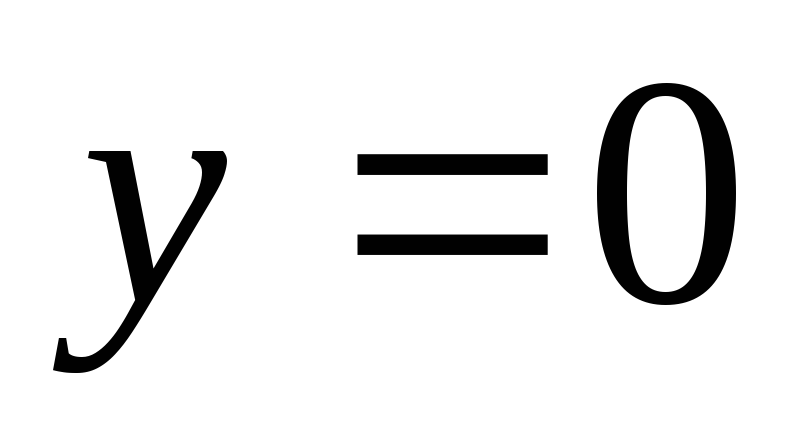
• х = а А(а; 0);

• при х > а у – мнимые таких точек нет.

Итак, частью эллипса, расположенной в I четверти, является дуга ВА. Отображая ее относительно обеих координатных осей, получаем весь эллипс.

Частным случаем эллипса является окружность при а = b эллипс можно получить из окружности радиуса а, сжатием её в а/b раз вдоль оси Оу.

Введем ещё одну величину, характеризующую форму эллипса.

Эксцентриситетом эллипса  называется отношение его фокального расстояния к длине большой оси, т.е.. Так как a > c, то 0 ≤ < 1.

Принимая во внимание, что , найдем при очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если ε близко к 1, то b мало по сравнению с числом а и эллипс вытянут вдоль большей оси. Таким образом, эксцентриситет характеризует меру вытянутости эллипса.

Две прямые, перпендикулярные большей оси эллипса и расположенные симметрично относительно центра на расстоянии от него, называются директрисами эллипса: и .

Теорема. Если r – расстояние от произвольной точки М эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса: , .