Уравнение прямой в полярных координатах

Уравнение прямой в полярных координатах ρ и :

ρ(Acos φ + Bsin φ) + C = 0

или

Тангенциальное уравнение прямой

Тангенциальное уравнение прямой на плоскости:

ξx + ηy = 1.

Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.

Уравнения прямой в пространстве

Векторное параметрическое уравнение прямой в пространстве:

где  — радиус-вектор некоторой фиксированной точки M₀, лежащей на прямой,  — ненулевой вектор, коллинеарный этой прямой,  — радиус-вектор произвольной точки прямой.

Параметрическое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Каноническое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Общее векторное уравнение прямой в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

 и 

то уравнение прямой можно задать системой этих уравнений:

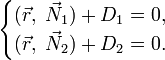
Взаимное расположение нескольких прямых на плоскости

Две прямые, заданные уравнениями

или

пересекаются в точке

Угол γ₁₂ между пересекающимися прямыми определяется формулой

При этом под γ₁₂ понимается угол, на который надо повернуть первую прямую (заданную параметрами A₁, B₁, C₁, k₁ и b₁) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.

Эти прямые параллельны, если A₁B₂ − A₂B₁ = 0 или k₁ = k₂, и перпендикулярны, если A₁A₂ + B₁B₂ = 0 или .

Любую прямую, параллельную A₁x + B₁y + C₁ = 0, можно выразить уравнением A₁x + B₁y + C = 0. При этом расстояние между ними будет равно

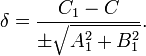
Если знак перед радикалом противоположен C₁, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.

Для того, чтобы три прямые

пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие

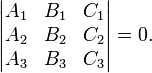
Если  и , то прямые  и  перпендикулярны.

3 Плоскость

Некоторые характеристические свойства плоскости

• Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

• Две плоскости являются либо параллельными, либо пересекаются по прямой.

• Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.

• Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.

• Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.

Уравнения плоскости

Впервые встречается у А. К. Клеро (1731).

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).

Нормальное уравнение ввёл Л. О. Гессе (1861).

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

• Общее уравнение (полное) плоскости

где  и  — постоянные, причём  и  одновременно не равны нулю; в векторной форме:

где  — радиус-вектор точки , вектор  перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :

Если один из коэффициентов в уравнении П. равен нулю, уравнение называется неполным. При  П. проходит через начало координат, при  (или , ) П. параллельна оси  (соответственно  или ). При  (, или ) П. параллельна плоскости  (соответственно  или ).

Уравнение плоскости в отрезках:

где , ,  — отрезки, отсекаемые П. на осях  и .

Уравнение плоскости, проходящей через точку  перпендикулярно вектору нормали :

в векторной форме:

Уравнение плоскости, проходящей через три заданные точки , не лежащие на одной прямой:

(смешанное произведение векторов), иначе

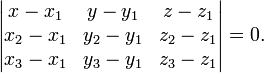
Нормальное (нормированное) уравнение плоскости

в векторной форме:

где - единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

(знаки  и  противоположны).

Определение по точке и вектору нормали

В трехмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.

Допустим, r₀ является радиусом-вектором точки P₀, заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка P с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от P₀ к P, перпендикулярен n.

Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:

 (Здесь точка означает скалярное произведение, а не умножение.)

Развернув выражение, мы получим:

что является знакомым нам уравнением плоскости.

Например: Дано: точка на плоскости P(2,6, − 3) и вектор нормали N(9,5,2).

Уравнение плоскости записывается так:

9(x − 2) + 5(y − 6) + 2(z + 3) = 0

− 18 + 9x − 30 + 5y + 6 + 2z = 0

9x + 5y + 2z − 42 = 0