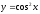- •II. Сприймання і усвідомлення знань про похідну сталої функції, степеневої функції з цілим показником
- •VI. Підведення підсумків уроку
- •V. Домашнє завдання
- •1) Знайдіть похідні функцій
- •2) Знайдіть похідні функцій:
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •3. Знайдіть похідні функцій:
- •IV. Сприймання і усвідомлення теореми про похідну частки функцій
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •V. Домашнє завдання
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •IV. Домашнє завдання
- •IV. Сприймання і усвідомлення матеріалу про похідну степеневої функції , де
1. Знайдіть похідні функцій:
а) у = (3х+2)50; б) (6-7х)10;
в)  ; г)
; г)  .
.
Відповідь: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2. Знайдіть похідні функцій:
а)  ; б)
; б)  ;
;
в) 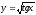 ; г)
; г)  .
.
Відповідь: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
ІІІ. Підведення підсумків уроку
При підведенні підсумків уроку можна скористатись таблицею.
Таблиця диференціювання
|
|
|
|
|
|
|
|
|
|
|
|
IV. Домашнє завдання
Розділ VII § 4. запитання і завдання для повторення до розділу VII № 23–28. вправа № 10 (6, 10, 14, 22).
ТЕМА УРОКУ: Похідна показникової, логарифмічної та степеневої функцій
Мета уроку: Формування знань учнів про похідну показникової, логарифмічної та степеневої функції(з довільним дійсним показником), умінь учнів в знаходженні похідних функцій.
І. Перевірка домашнього завдання
1.Перевірити правильність виконання домашніх вправ за записами, зробленими на дошці.
6)  ;
;
10)  ;
;
11)  ;
;
22) 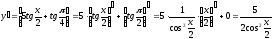 .
.
2. Виконання усних вправ.
Знайдіть похідні функцій, які подано в таблиці.
Таблиця
|
|
1 |
2 |
3 |
4 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
ІІ. Сприймання і усвідомлення матеріалу про похідну показникової функції
Перш
ніж знаходити похідну показниковїх
функції, зробимо два важливих зауваження.
Графік функції у=ах
проходить через точку (0; 1). Нехай
 – величина кута , утвореного дотичною
до графіка функції у = ах
в точці (0; 1)з додатним напрямом осі
абсцис. Величина цього кута залежить
від значення основи а. Наприклад,
обчислено, що при а = 2 величина кута
– величина кута , утвореного дотичною
до графіка функції у = ах
в точці (0; 1)з додатним напрямом осі
абсцис. Величина цього кута залежить
від значення основи а. Наприклад,
обчислено, що при а = 2 величина кута
 приблизно
дорівнює 340(рис.29),
а при а = 2,
приблизно
дорівнює 340(рис.29),
а при а = 2,
 =470.
=470.
у у
= ех
якщо основа а показникової функції у =
ах
зростає від 2 до 3, то величина кута
 зростає і приймає значення від 340
до 470.
Отже, існує таке значення
зростає і приймає значення від 340
до 470.
Отже, існує таке значення
 ,
при якому дотична,
проведена до графіка функції у = ах
в точці (0; 1)
утворює з додатним напрямком осі ОХ кут
450
(рис.31). Таке значення
,
при якому дотична,
проведена до графіка функції у = ах
в точці (0; 1)
утворює з додатним напрямком осі ОХ кут
450
(рис.31). Таке значення
 прийнято позначати буквою е, е – число
ірраціональне, е = 2,718281828459...
прийнято позначати буквою е, е – число
ірраціональне, е = 2,718281828459...
 0
0
Таким чином, дотична до графіка функції у = ех в точці (0; 1) утворює з додатним напрямком осі абсцис, який дорівнює 450.
У
відповідності з геометричним змістом
похідної даний висновок означає, що
значення похідної функції
 в точці х0
дорівнює
в точці х0
дорівнює
 =1.
Отже,
=1.
Отже,
 .
.
Знайдемо
тепер формулу похідної функції
 .
.
Нехай
аргумент х0
одержав приріст
 ,
тоді:
,
тоді:
1) 
2) 
3)  .
.
Таким
чином, похідна функції ех
дорівнює самій функції:

Знайдемо
похідну функції
 ,
скориставшись основною логарифмічною
тотожністю та правилом знаходження
похідної складеної функції:
,
скориставшись основною логарифмічною
тотожністю та правилом знаходження
похідної складеної функції:
 .
.
Отже,
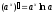
Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи.
Приклад 1. Знайдіть похідну функцій:
а) у
= 5х; б) у
= е3-2х; в) 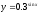 ; г)
; г)  .
.
Розв’язання
а)  ;
;
б)  ;
;
в)  ;
;
г)
 .
.
Виконання вправ.
№ 2 (2, 4, 6, 8, 10, 12), №2 (20, 22, 24, 26, 28, 30) із підручника (розділ Х).
ІІІ. Сприймання і усвідомлення матеріалу про похідну логарифмічної функції
Розглянемо
функцію
 .
За основною логарифмічною тотожністю:
.
За основною логарифмічною тотожністю:
 для всіх додатних х.
для всіх додатних х.
Диференціюючи
обидві частини цієї рівності, одержимо:
 ,
або
,
або
 .
.
Звідси
 .
.
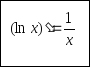 Отже,
Отже,
Знайдемо
похідну функції
 .
Так як
.
Так як
 ,
то
,
то


 .
.
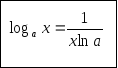 Отже,
Отже,
Приклад 1. Знайдіть похідну функцій:
а) 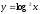 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
а) ![]()
 ;
;
б)  ;
;
в) 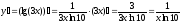 ;
;
г)

=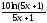 .
.
Виконання вправ.
№ 2 (14, 16, 18, 32, 34, 36, 38, 40, 42), із підручника (розділ Х).



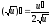



 ,де
,де



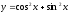
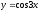



 =
=