
- •II. Сприймання і усвідомлення знань про похідну сталої функції, степеневої функції з цілим показником
- •VI. Підведення підсумків уроку
- •V. Домашнє завдання
- •1) Знайдіть похідні функцій
- •2) Знайдіть похідні функцій:
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •3. Знайдіть похідні функцій:
- •IV. Сприймання і усвідомлення теореми про похідну частки функцій
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •V. Домашнє завдання
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •IV. Домашнє завдання
- •IV. Сприймання і усвідомлення матеріалу про похідну степеневої функції , де
ТЕМА УРОКУ: Похідні елементарних функцій
МЕТА УРОКУ: формування знань учнів про похідну сталої функції, степеневої функції з цілим показником, тригонометричних функцій.
І Перевірка домашнього завдання
1. Три учні відтворюють розв’язування вправ № 1 (1,2), 2.
1)
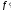 =
=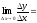
 =
=
2)
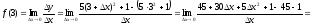
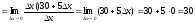
Рівняння
шуканої дотичної у – у0
=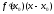 .
Оскільки х0
= 1, у = х2,
то
.
Оскільки х0
= 1, у = х2,
то
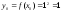 і
і
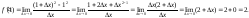
Отже, у – 1 = 2 (х -1) або у = 2х – 1.
2. Фронтальна бесіда за запитаннями №№ 11 – 17 із Запитання і завдання до розділу VII.
II. Сприймання і усвідомлення знань про похідну сталої функції, степеневої функції з цілим показником
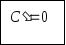 На
попередньому уроці ми довели, що похідна
лінійної функції у =
На
попередньому уроці ми довели, що похідна
лінійної функції у =
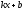 дорівнює
дорівнює
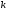 ,
тобто
,
тобто
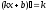 .
.
Якщо
покласти
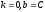 ,
де С – довільна постійна, то одержимо,
що тобто похідна постійної функції
дорівнює 0.
,
де С – довільна постійна, то одержимо,
що тобто похідна постійної функції
дорівнює 0.
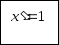 Якщо
у формулі
Якщо
у формулі
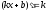 покласти
покласти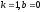 ,
то одержимо
,
то одержимо
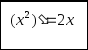 Нам
уже відомо, що . А як знайти похідну
функції у = х5,
у = х20
тощо? Розглянемо функцію у= хn,
де n
–
Нам
уже відомо, що . А як знайти похідну
функції у = х5,
у = х20
тощо? Розглянемо функцію у= хn,
де n
–
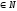 .
.
Знайдемо
похідну цієї функції, для цього зафіксуємо
значення аргумента х0
і надамо йому приросту
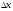 ,
тоді:
,
тоді:
1) 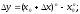
2) 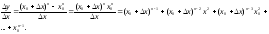
(Скориставшись
формулою

3)

 Звідси
Звідси
Розглянемо
функцію у = хn-1,
де
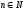 .
.
Знайдемо
похідну цієї функції, для цього зафіксуємо
значення аргумента х0
і надамо йому приросту
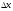 ,
тоді
,
тоді
1) 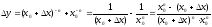
2) 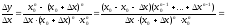
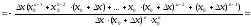

3) 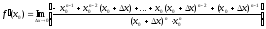 =
=
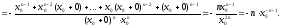
Отже,
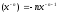 ,
де
,
де
 .
.
Таким
чином виконується рівність:
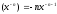 .
.
Виконання вправ
1. Знайдіть похідну функції:
а)
у = х6; б)
у = х8; в)
у = х2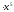 ; г)
; г)
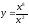 .
.
Відповідь: а) 6х5; б) 8х7; в) 7х6; г) 6х5.
2. Знайдіть похідні функцій:
а)
у = х-10; б)
у = х2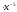 ; в)
; в)
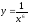 ; г)
; г)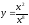 .
.
Відповідь: а) -10х-11; б) -3х-4; в) -6х-7; г) -6х-7.
ІІІ. Сприймання і усвідомлення знань про похідну тригонометричних функцій
Знайдемо
похідну функції у=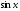 .
Зафіксуємо х0
і надамо аргументу приросту
.
Зафіксуємо х0
і надамо аргументу приросту
 ,
тоді:
,
тоді:
1) 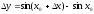
2)
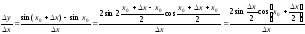
3) 
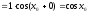 .
.
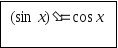 Отже
Отже
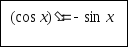 Аналогічно
можна довести, що
Аналогічно
можна довести, що
Знайдемо
похідну функції
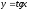 .
.
Зафіксуємо
х0
і надамо аргументу приросту
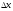 ,
тоді:
,
тоді:
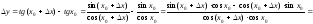
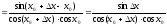 .
.
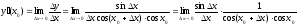
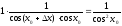 .
.
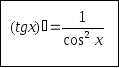 Отже,
Отже,
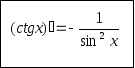 Аналогічно
можна довести, що
Аналогічно
можна довести, що
Виконання вправ № 1 (3), 5 із підручника.
VI. Підведення підсумків уроку
Провести підведення підсумків уроку з використанням таблиці 4 похідних.
Таблиця
Таблиця похідних

V. Домашнє завдання
Розділ VІІ § 3. запитання і завдання для повторення розділу VІІ № 19 – 22. вправа №4 (2, 4).
ТЕМА УРОКУ: Теореми про похідну суми, добутку і частки функцій
МЕТА УРОКУ: Вивчення теореми про похідні суми, добутку і частки функцій, формування умінь учнів у знаходження похідних.
І. Перевірка домашнього завдання
1. Усне розв’язування вправ.
1) Знайдіть похідні функцій
а)
у – х10; б)
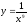 ; в)
; в)
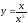 ; г)
; г)
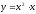 .
.
Відповідь: а) 10х9; б) -9х-10; в) -4х-5;ё г) 3х2.
2) Знайдіть похідні функцій:
а)
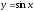 в точці
в точці
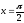 ; б)
; б)
 в точці
в точці
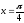 ;
;
в)
 в точці
в точці
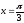 ; г)
; г)
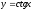 в точці
в точці
 .
.
Відповідь:
а) 0; б)
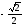 ; в)
4; г) -1.
; в)
4; г) -1.
2. Відповісти на запитання, що виникли у учнів під час виконання домашніх вправ.
ІІ. Сприймання і усвідомлення теореми про похідну суми функції
Теорема: Якщо функції f(x) і g(x) диференційовані в точці х, то їхня сума диференційована в цій точці і
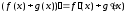
або коротко говорять: похідна суми дорівнює сумі похідних.
Доведення
Розглянемо
функцію
 у
= f(x)
+ g(x).
у
= f(x)
+ g(x).
Зафіксуємо
х0
і надамо аргументу приросту
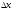 .
Тоді
.
Тоді
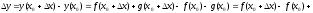
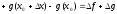 ,
,
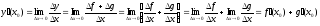 .
.
Отже,
 .
.
Наслідки
а) Похідна різниці дорівнює різниці похідних.
Нехай
у(х) = f(x)
-
g(x),
тоді f(x)
= у(х) +
g(x)
і
 ,
звідси
,
звідси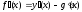 .
.
б) Похідна суми декількох функцій дорівнює сумі похідних цих фукцій, тобто
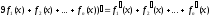 .
.
Приклад. Знайдіть похідну функцій
а)
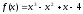 ;
;
б)
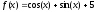 ;
;
в)
 .
.
Розв’язання
а)
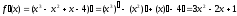 ;
;
б)
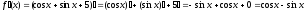 .
.
в)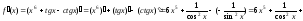
 .
.
Відповідь:
а)
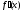
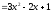 ; б)
; б)
 в)
в)
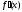 =
=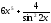 .
.
Виконання вправ
