5. Пример курсовой работы

Содержание курсовой работы рассмотрим на примере: “Оценка погрешности и уточнение методом Ромберга результатов численного дифференцирования по центрально-симметричной разностной формуле второго порядка”. В качестве дифференцируемой функции выберем при x=0.5.

5.1. Описание численного метода дифференцирования по центрально-симметричной разностной формуле второго порядка (см.п. 3).

5.2. Программная реализация метода дифференцирования по центрально-симметричной разностной формуле второго порядка (прилагается листинг программы с комментариями).

5.3. Оценка погрешности результата, уточнение результата, визуализация результатов уточнения.

5.3.1. В результате выполнения программы реализующей численное дифференцирование функции , были получены следующие результаты z_n при следующих n (прил. П3.2)

При этом на каждом шаге происходит увеличение числа разбиений в 2 раза, т.е. Q=2.

5.3.2. Далее определяется разница результата на следующем и предыдущем шаге (прил. П3.3)

5.3.3. Вычисляем отношения (прил. П3.3.1)

5.3.4. Потом экстраполируем полученный результат (прил. П3.3.2):

• Для метода Ромберга определяем порядок точности метода из приближенного равенства Q^kK_n. Проводим экстраполяцию по формуле Ричардсона

;

• Для метода Эйткена для экстраполяции используется полученные значения K_n

.

Далее шаги 2,3 повторяются, до тех пор, пока . Нарушение этого равенства свидетельствует о том, что дальнейшее уточнение результата невозможно.

5.3.5. Строятся графики в логарифмической шкале:

a) Строится график полученных результатов в сравнении с точным результатом. По оси абсцисс откладывается lgn, по оси ординат значения , , ….

Полученные результаты прилагаются (прил. П3.3.3).

b) Строится график полученных результатов в сравнение с “эталонным” значением. В качестве эталона выбирается наиболее точный результат z, полученный в результате последней экстраполяции. По оси абсцисс откладывается lgn, по оси ординат значения , , ,…

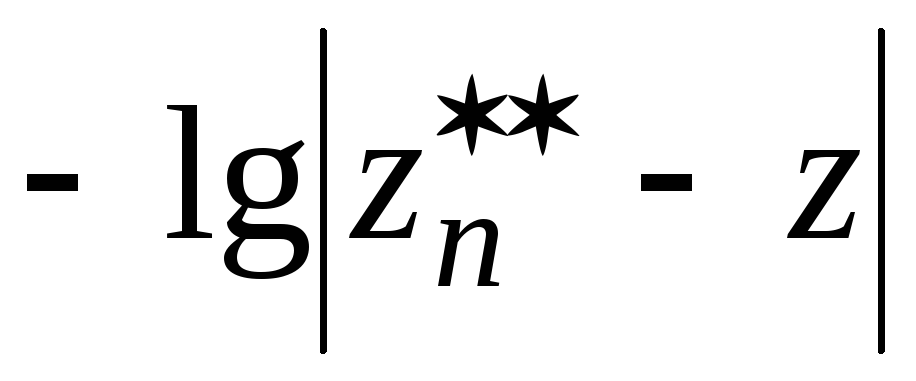Полученные результаты прилагаются (прил. П3.3.4).

c) Оценка результатов производится по правилу Рунге , ,… Строится график полученных результатов,

По оси абсцисс откладывается log₁₀n, по оси ординат значения -log₁₀, -log₁₀, …

Образец оформления титульного листа

пояснительной записки

Министерство образования и науки Российской Федерации федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

Уфимский государственный авиационный технический университет

Кафедра компьютерной математики

Пояснительная записка

к курсовой работе по дисциплине

«Языки и технология программирования»

Численное дифференцирование функций.

Уточнение методами Ромберга и Эйткена.

Выполнил: студ. гр. _____ Ф.И.О.

Проверил: ……………….доц. К.ф.-м.н. Зиннатуллина О.Р.

Уфа 2011

П3.1. Графический интерфейс программы

Рис. П3.1. График искомой функции y(z)

Рис. П3.2. Оценка погрешности численных результатов

П3.2.Численные результаты

ni	zn
1	-.8068453602226698
2	-.8594512716504229
4	-.8730213311404762
8	-.8764404712456473
16	-.8772969276777106
32	-.8775111463634158
64	-.8775647075727431
128	-.8775780982837214
256	-.8775814459870084
512	-.8775822829144317
1024	-.8775824921463595
2048	-.8775825444545262
4096	-.8775825575312410
8192	-.8775825608026935
16384	-.8775825616321526
32768	-.8775825618649833
65536	-.8775825621560216
131072	-.8775825621560220
262144	-.8775825649499893
524288	-.8775825649499880

П3.3. Оценка и уточнение численных результатов

ni
1
2	-0.052605911
4	-0.013570059
8	-0.003419140
16	-0.000856456
32	-0.000214219
64	-5.35612E-05
128	-1.33907E-05
256	-3.34770E-06
512	-8.36927E-07
1024	-2.09232E-07
2048	-5.23082E-08
4096	-1.30767E-08
8192	-3.27145E-09
16384	-8.29459E-10
32768	-2.32831E-10
65536	-2.91038E-10
131072	-9.99201E-16
262144	-2.79397E-09
524288	9.99201E-16

П3.3.1. Коэффициент уменьшения погрешности при удвоении n

ni
1
2
4	3.87661612
8	3.96885155
16	3.99219386
32	3.99804727
64	3.99951174
128	3.99987793
256	3.99996948
512	3.99999235
1024	3.99999862
2048	3.99998585
4096	4.00009994
8192	3.99722052
16384	3.94407947
32768	3.56249395
65536	0.80000175
131072	291270.889
262144	3.5763E-07
524288	-2796201.9

П3.3.2. Вычисление экстраполированного значения

ni
1
2	-0.876986575
4	-0.877544684	-0.000558109
8	-0.877580185	-3.55003E-05	15.72124
16	-0.877582413	-2.22854E-06	15.92984
32	-0.877582553	-1.39437E-07	15.98243
64	-0.877582561	-8.71720E-09	15.99560
128	-0.877582562	-5.44861E-10	15.99894
256	-0.877582562	-3.40566E-11	15.99868
512	-0.877582562	-2.13496E-12	15.95190
1024	-0.877582562	-9.63674E-14	22.15438
2048	-0.877582562	-2.46692E-13	0.390639
4096	-0.877582562	4.35652E-13	-0.566260
8192	-0.877582562	-3.03102E-12	-0.143730
16384	-0.877582562	-1.54612E-11	0.196041
32768	-0.877582562	-3.39551E-11	0.455343
65536	-0.877582562	-3.10440E-10	0.109377
131072	-0.877582562	9.70114E-11	-3.200040
262144	-0.877582566	-3.72529E-09	-0.026040
524288	-0.877582565	9.31324E-10	-3.999990

П3.3.3. Результат экстраполяции в сравнении с точным значением

Рис. П3.3. Результат экстраполяции в сравнении с точным значением

П.3.3.4. Результат экстраполяции в сравнении с “эталонным” значением

Рис. П3.4. Результат экстраполяции в сравнении с “эталонным” значением

П3.3.5. Результат экстраполяции с оценкой погрешности по правилу Рунге (сравнением с «правым соседом»)

Рис. П3.5. Результат экстраполяции с оценкой погрешности по правилу Рунге

Литература

1. Программная реализация численных методов: Методические указания к курсовой работе по дисциплине «Вычислительный эксперимент и методы вычислений» / Уфимск. гос. авиац. техн. ун-т; Сост.: В.П. Житников, О.Р. Зиннатуллина, А.А. Михтанюк. – Уфа, 2007. – 34 с.